Download PDF file - Telektronikk

More documents

Recommendations

Info

angi prognoser for akkumulert produksjonsvolum ved tidspunkt T. Dette uttrykket kan så settes inn i Wrights utvidet lærekurvemodell, og vi får: (5.3) Dette uttrykket angir da prisprognose for nettkomponenter gitt at n er akkumulert produksjonsvolum. Hvis vi isteden benytter Crawfords utvidede lærekurvemodell der er definert som antall enheter produsert i en serie ved tidspunkt t, vil vi få andre formler for prisprognosen. La igjen n(1), n(2), ..., n(s) være det akkumulerte produksjonsvolum. Da vil: n*(t) = n(t) - n(t-1) (5.4) Med andre ord, differansen mellom akkumulert produksjonsvolum ved tidspunkt t og t-1, angir hvor stort produksjonsvolumet er ved tidspunkt t. Av likning (5.4) og likning (5.2) får vi følgende: ˆn(T )* = ˆM 1 + e â+ ˆ − ˆg ⎛ bT ⎞ ⎜ ⎟ − ⎝ ⎠ ˆ M 1 + e â+ ˆ − ˆg ⎛ b(T −1) ⎞ ⎜ ⎟ ⎝ ⎠ ˆn ˆP n(T ) = ˆα t * ˆ M 1 + e â+ ˆ − ˆg β ˆ ⎡ ⎤ ⎢ ⎛ bT ⎞ ⎜ ⎟ ⎥ ⎢ ⎝ ⎠ ⎥ ⎣ ⎦ (5.5) Dette uttrykket settes så inn i Crawfords utvidede lærekurvemodell og vi får: ˆP n(T ) = ˆα (5.6) Dette uttrykket angir da prisprognose for nettkomponenter gitt at n*(t) er produksjonsvolum pr tidsintervall. ˆ M 1 + e â+ ˆ − ˆg ⎛ bT ⎞ ⎜ ⎟ − ⎝ ⎠ ˆ M 1 + e â+ ˆ ⎡ − ˆg ⎤ ⎢ ⎛ b(T −1) ⎞ ⎜ ⎟ ⎥ ⎢ ⎝ ⎠ ⎥ ⎣ ⎦ 6 Praktisk fortolkning av prognosemodellen β ˆ Vi skal nå vise hvorledes prognosemodellen kan benyttes for å beskrive pris på komponenter som funksjon av tiden og se på betydningen av de parametrene som inngår. Spesielt når det dreier seg om nye komponenter som bare foreligger i form av prototyper eller hvor produksjonen er helt i startfasen er det viktig å ha en modell som en kan analysere og benytte for å gjøre gode antakelser om prisutvik- Relativt akkumulert volum 1,00 0,80 0,60 0,40 0,20 lingen. Det er derfor viktig å forstå hva parametrene betyr i modellen. En viktig konsekvens som vi kan trekke av å kombinere en logistisk modell som i likning (5.1), (hvor vi for enkelhets skyld setter g = 1 som konstant), med en lærekurve som i likning (3.1) Pn(t) = αn(t) β (6.1) er at det ikke vil være nødvendig å beskrive n(t) som et globalt akkumulert volum, men vi kan nøye oss med den relative prognosen (6.2) hvor nr (t) går fra 0 til 1. Dette betyr at vi f eks kan benytte volumprognoser i et enkelt land eller i noen storbyer hvor anvendelsen av komponenten kan antas å være representativ for den globale utviklingen. Det betyr at en ikke trenger informasjonen om det totale globale produksjonsvolum (eller akkumulert globalt volum) som det kan være vanskelig å få data på. 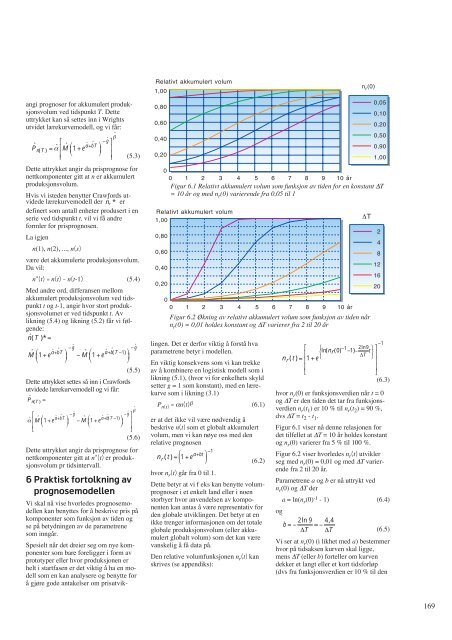Den relative volumfunksjonen nr (t) kan skrives (se appendiks): nr (t )= ( 1 + ea+bt ) −1 n r (0) 0,05 0,10 0,20 0,50 0,90 1,00 0 0 1 2 3 4 5 6 7 8 9 10 år Figur 6.1 Relativt akkumulert volum som funksjon av tiden for en konstant ∆T = 10 år og med nr (0) varierende fra 0,05 til 1 Relativt akkumulert volum 1,00 0,80 0,60 0,40 0,20 0 0 1 2 3 4 5 6 7 8 9 10 år Figur 6.2 Økning av relativt akkumulert volum som funksjon av tiden når nr (0) = 0,01 holdes konstant og ∆T varierer fra 2 til 20 år ∆T 2 4 8 12 16 20 ln(nr(0) nr (t )= 1 + e (6.3) −1−1)− 2ln9 ∆T t −1 ⎡ ⎧ ⎫ ⎤ ⎢ ⎨ ⎬ ⎩ ⎭ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ hvor nr (0) er funksjonsverdien når t =0 og ∆T er den tiden det tar fra funksjonsverdien nr (t1 ) er 10 % til nr (t2 ) = 90 %, dvs ∆T = t2 - t1 . Figur 6.1 viser nå denne relasjonen for det tilfellet at ∆T = 10 år holdes konstant og nr (0) varierer fra 5 % til 100 %. Figur 6.2 viser hvorledes nr (t) utvikler seg med nr (0) = 0,01 og med ∆T varierende fra 2 til 20 år. Parametrene a og b er nå uttrykt ved nr (0) og ∆T der a = ln(nr (0) -1 - 1) (6.4) og 2ln9 b = − ∆T (6.5) Vi ser at nr (0) (i likhet med a) bestemmer hvor på tidsaksen kurven skal ligge, mens ∆T (eller b) forteller om kurven dekker et langt eller et kort tidsforløp (dvs fra funksjonsverdien er 10 % til den ≈−4,4 ∆T 169
n r (t) 90 % 10 170 1,00 0,80 0,60 0,40 t 1 ∆T Figur 6.3 Illustrasjon av de størrelsene som inngår i likning (6.3) 1,00 0,80 0,60 0,40 0,20 0 0 t 2 Normalisert pris tid 0,20 0 0 2 4 6 8 10 2 20 år 8 14 ∆T Figur 6.4 Utvikling av normalisert komponentpris i tid for nr (0) = 0,001 og K = 0,95 Normalisert pris 2 0.01000 4 6 n år 8 0.00001 r (0) 10 Figur 6.5 Normalisert pris som funksjon der tiden for forskjellige verdier av nr (0) og med ∆T = 10 år, K = 0,95 som konstanter er 90 % av maksimalverdien). Figur 6.3 demonstrerer denne relasjonen. Vi vil nå vise at vi bare trenger den relative prognosefunksjonen i prisfunksjonen. La oss starte med den absolutte verdien gitt i likning (5.1) for akkumulert volum n(t). Prisen pr enhet kan da skrives: P(t) = α n(t) β (6.6) hvor P(t) betyr Pn(t) . La oss nå sette inn t = 0 og vi får prisen pr enhet i referanseåret: P(0) = αn(0) β (6.7) Ved å dele uttrykket (6.6) på (6.7) får vi β P(t ) ⎡ n(t ) ⎤ = ⎢ ⎥ P(0) ⎣n(0) ⎦ (6.8) eller P(t )= P(0) (6.9) der de absolutte funksjonsverdiene n(t) erstattes av de relative verdiene nr (t) siden n β ⎡ r (t ) ⎤ ⎢ ⎥ ⎣n r (0) ⎦ n(t ) n(0) (6.10) Ved å sette inn likning (6.3) i (6.9) blir det fullstendige uttrykket for pris pr enhet som funksjon av tid. = nr (t ) nr (0) P(t )= P(0) nr (0) −1 ln nr(0) 1 + e −1 ⎛ ⎞ ⎜ −1⎟ − ⎝ ⎠ 2ln9 ∆T t log2K ⎛ −1⎞ ⎡ ⎧ ⎫ ⎤ ⎜ ⎢ ⎨ ⎬ ⎩ ⎭ ⎥ ⎟ ⎜ ⎢ ⎥ ⎟ ⎜ ⎢ ⎥ ⎟ ⎝ ⎣ ⎦ ⎟ ⎠ (6.11) som inneholder de fire størrelsene P(0), nr (0), ∆T og K. Det er egentlig bare nr (0) og ∆T som må prognostiseres. Prisen i referanseåret P(0) og lærekurvekoeffisientene K er mer eller mindre kjent. For å illustrere denne prisfunksjonen setter vi P(0) = 1 (normalisert pris) og K = 0,95 konstant. Figur 6.4 viser hvorledes normalisert pris varierer ved å holde nr (t) = 0,001 og la ∆T variere fra 2 til 20 år. Figur 6.5 viser likeledes hvorledes normalisert pris utvikler seg for forskjellige nr (0) ved å holde ∆T og K = 0,95 konstant. 7 Anvendelse av den utvidede prognosemodellen i teknisk økonomisk analyse Det europeiske RACE-prosjektet TITAN, som står for “Tool for Introduction scenario & Techno-economic evaluation of Access Network”, har valgt å benytte den utvidede prognosemodellen som grunnlag for sine beregninger [7], [8], [9]. Dette prosjektet har som målsetting å evaluere forskjellige introduksjonsscenarier for fiber i aksessnettet. Prosjektet har utviklet et PC-basert pro- gram for beregning av lønnsomheten av de forskjellige scenarier som man ønsker å studere. Fokus er på en studieperiode av 10 år (f eks 1995–2005) og tar for seg privatmarkedet og de små bedriftskunder. Det fokuseres på aksessnettet som er den mest følsomme delen av hele nettet med hensyn til kostnadene, og som dessuten er den delen av nettet som er mest avhengig av hvorledes behovet/ etterspørselen etter tjenester blir i fremtiden. Forskjellige systemalternativer studeres og beregningen som gjøres legges til grunn for planleggingen av fremtidig utbygging, med utgangspunkt i den teknologien som finnes i dag. Prosjektet kan deles i tre deler: 1 Utviklingen av et fleksibelt regneprogram med en (eller flere) geometriske modeller som gir et mål på materiell, installerings- og gravekostnader, kostnader for utstyr og vedlikehold. Det tas hensyn til avskrivninger og andre økonomiske faktorer. Alle beregninger relateres til nåverdier. Det legges inn prognoser for tjenesteutvikling og inntjeningsmuligheter og det gjøres følsomhetsanalyser der effekten av mer eller mindre ekstreme avvik fra prognosene studeres. 2 Prosjektet studerer prognoser for de tjenestene som man tror vil være de viktigste drivkreftene i privatmarkedet. Man deler tjenestene inn i båndbreddekategorier og søker å prognostisere potensielt behov avhengig av hva tjenestene vil koste. Videre transformeres disse prognosene til behov som funksjon av tid ved hjelp av de pris-/kostnadsmodellene som er utviklet. Som en del av dataunderlaget for tjenestebehovsprognoser blir det gjennomført en “Delphi-studie” med ca 100 eksperter involvert. Resultatene korreleres med andre metoder for prognoser. 3 Den siste delen av TITAN består i å beskrive de aktuelle arkitekturer som skal studeres. Det er for eksempel FTTH (fiber til hjemmene), FTTC (fiber til grøftekanten) med kopper eller radio drop. Disse løsningene sammenliknes med tradisjonelle kopperløsninger. Det er også av interesse å studere forskjellige oppgraderinger av bestående arkitekturer, både koaksialkabelnett og parkabelløsninger. TITAN-prosjektet tar utgangspunkt i at alle kunder vil ha vanlig telefoni (POTS).
Page 1 and 2: 001.18:621.39 166 Prognoser for pri
Page 3: 168 der ˆσ β* = ˆσ = ˆy t =
Page 7: ønsker å benytte disse metodene f

Download PDF file - Telektronikk

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?