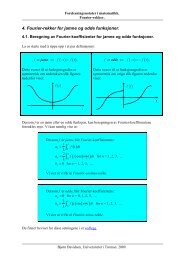
Potensrekker, Taylor-rekker. - Universitetet i Tromsø

Matematikk 2 og statistikk - studieveiledning.
Generelt om tallfølger og rekker. Side 1.
Alle henvisningene til lærebok gjelder Per-Even Kleive: Matematiske metoder 2, 3.
utgave. Henvisninger i parentes gjelder 2. utgave.
Rekker der leddene avhenger av en fri variabel.
Læreboka starter i eks. 3.1 med å merke seg at den geometriske rekka
2 3
1+ x+ x + x + + x n +
1
har summen forutsatt at rekka konvergerer, altså når − < <
1− x 1 x 1.
Vi kan altså skrive
1
2 3
n 1
= 1+ x+ x + x + + x + = når − 1< x < 1.
1−
x 1 − x
Læreboka uttrykker seg mer forsiktig: Den sier at rekka "konvergerer mot"
ledd går mot uendelig.
1
1− x
når antall
Hopp over eks. 3.2. Regn heller oppgave 3.1, 3.3. I begge disse oppgavene er det
geometriske rekker, slik at du må finne kvotienten k, og bestemme hvilke x-verdier som gjør
at − 1< k < 1.
Vi forlater nå de geometriske rekkene, og går over til å se på potensrekker. Og disse rekkene
skal vi holde oss til i resten av kapitlet og i kap. 4. En enkel form for en potensrekke er gitt i
definisjon 3.1. En mer generell definisjon er gitt i definisjon 3.2.
Før vi går videre, vil jeg si litt om hvorfor vi maser om disse potensrekkene. I eks. 3.1 så vi at
1
funksjonen kan skrives som ei potensrekke når x ligger innenfor et konvergensintervall
1− x
(den geometriske rekka i det eksemplet er også ei potensrekke). Nå viser det seg at svært
mange funksjoner kan skrives som slike potensrekker, iallfall når x ligger innenfor et visst
intervall. Dersom vi tar med et endelig antall ledd i rekka, vil rekka tilnærmet være lik
funksjonen. Og slike rekkeutviklinger av funksjoner er faktisk nyttig i mange situasjoner.
Vi må altså ta for oss to problem:
1) Hvordan kan vi finne potensrekka til en funksjon f x Behandles i kap. 4 (og 3.5).
2) For hvilke x-verdier konvergerer rekka mot f x Behandles i resten av kap. 3.
Læreboka starter omtalen av konvergens av potensrekker med setning 3.1. Det intervallet der
rekka konvergerer, kalles konvergensintervallet. Halve bredden av dette intervallet blir
konvergensradien, se definisjon 3.3.
• Vi finner konvergensintervallet ved hjelp av forholdskriteriet (kap. 2.11 (2.10)).
• Endepunktene av konvergensintervallet må undersøkes spesielt.
Eks. 3.3 kan danne mønsteroppskrift for en slik konvergensundersøkelse.
Gå gjennom eks. 3.3 og 3.4, og du vil se at mønsteret fra eks. 3.3 går igjen.
Oppgave 3.5 a,b,c,e.
b g
b g
Bjørn Davidsen, Universitetet i Tromsø. 2009.

Matematikk 2 og statistikk - studieveiledning.
Generelt om tallfølger og rekker. Side 2.
∞
∑ kb
n=
1
Kap. 3.4 er stort sett bare repetisjon av kap. 3.3, men med den generelle rekka c x−
a .
Du finner konvergensintervallet for rekka på samme måte som før, bare med den lille
forskjellen at x blir erstattet av x − a . Etter at du har funnet konvergensintervallet for
x − a , legger du til a på begge sider av likhetstegnet. Se eks. 3.6 - 3.8.
Oppgave 3.6 a,c.
Kap. 3.5 kan virke litt uoversiktlig. Hovedpoengene er:
2
b g b g b g b g n
Anta at f x = c0 + c1 x− a + c2
x− a + + cn
x− a +
innenfor et konvergensintervall. Innenfor dette intervallet kan vi da:
• derivere på begge sider (setning 3.4 (3.5)):
dfbg x
c cbx ag n cnbx ag n −1
=
1
+ 2
2
− + + ⋅ − +
dx
• integrere på begge sider (setning 3.5 (3.4)):
z
x
c1 2 c2 3 cn
n+
1
fbg t dt = c0bx− ag+ bx− ag + bx− ag + +
bx− ag
+
a
2 3 n + 1
Vi får da nye potensrekker med samme konvergensradius som rekka til f x .
Hopp over eks. 3.9 og 3.10. I eks. 3.11 starter vi med at
1
2
= 1+ x+ x + + x n + når − 1< x < 1.
1−
x
Integrerer på begge sider:
zx
1 1 2 1 3 1
= + + + + +
0 1−
t dt x 2
x 3
x n x n
zx
1
Men =− 1−
0 1−
t dt lnb x g . Innsetting og fortegnsskift gir at
1 2 1 3 1
lnb1
− x g= − x − − − − −
2
x 3
x
n x n når − 1< x < 1.
Og dermed har vi funnet potensrekka til funksjonen fbxg = lnb1 − xg
når − 1< x < 1.
Det samme skjer i eks. 3.12 (3.10). Vi starter med at
1
2 4 6
= 1− x + x − x + når − 1< x < 1 (geometrisk rekke).
2
1 + x
Så integrerer vi på begge sider, og ender opp med ei potensrekke for arcus tangens:
3 5 7
x x x
arctan x = x− + − + når − 1< x < 1.
3 5 7
(Slutten av eksemplet om Gregorys formel kan du hoppe over).
Prøv selv å løse eks. 3.13 før du ser på løsningen (eksemplet er mer rotet i 2. utgave).
Du kan (foreløpig) hoppe over Eks. 3.14 og 3.15. Gå heller gjennom Eks. 3.16 som gjelder
derivasjon av potensrekker (bruk av setning 3.4).
Her kommer et eksempel til: Vi starter (som så ofte før) med at
b g
g
k
Bjørn Davidsen, Universitetet i Tromsø. 2009.

Matematikk 2 og statistikk - studieveiledning.
Generelt om tallfølger og rekker. Side 3.
1
2
= 1+ x+ x + + x n + når − 1< x < 1.
1−
x
Deriverer på begge sider:
1
2 −1
= 1+ 2x+ 3x + + nx n + når − 1< x < 1.
2
b1
− xg
1
Og dermed har vi funnet ei potensrekke for fbg
x =
2
1−
x
når − 1< x < 1.
I noen av eksemplene ovenfor foretar vi operasjoner på slike potensrekker. Setning 3.6 og 3.7
kommer da til anvendelse. Se også eks. 3.14 og 3.17.
Et eksempel til: Jeg har nettopp vist at
1
2 −1
= 1+ 2x+ 3x + + nx n + når − 1< x < 1.
2
b1
− xg
Multipliserer med x på begge sider, og får
x
2 3
= x+ 2x + 3x + + nx n + når − 1< x < 1.
2
b1
− xg
x
Og dermed har vi funnet ei potensrekke for fbg
x =
2
b1−
xg
når − 1< x < 1.
Oppgave 3.9.
b
g
Taylor- og Maclaurin-rekker.
Vi skal nå finne potensrekker for en funksjon
∞
∑
fbxg
k
• Rekker av formen cx kalles Maclaurin-rekker.
k
k = 1
∞
∑ kb
k = 1
• Rekker av formen c x−
a kalles Taylor-rekker.
g
k
på en systematisk måte. Litt terminologi:
• Dersom rekkene inneholder et endelig antall ledd, kalles de henholdsvis Maclaurinpolynom
og Taylor-polynom.
Vi ser at Maclaurin-rekker er spesialtilfeller av Taylor-rekker. Vi bruker derfor "Taylorrekke"
som et generelt uttrykk som også omfatter Maclaurin-rekker.
Læreboka starter med å konstruere Maclaurin-polynom (se definisjon 4.1). Denne
definisjonen er viktig, fordi den danner grunnlaget for alt videre arbeid med Maclaurin- og
Taylor-rekker. Poenget er nå at Maclaurin-polynomet er tilnærmet lik fbxg
, men at
tilnærmingen blir stadig bedre etter som antall ledd øker. Når antall ledd går mot uendelig, vil
Maclaurin-polynomet (som nå er blitt ei Maclaurin-rekke) konvergere mot fbxg
. Se eks. 4.1,
4.2 og 4.3.
Oppgave 4.1, 4.3.
Bjørn Davidsen, Universitetet i Tromsø. 2009.

Matematikk 2 og statistikk - studieveiledning.
Generelt om tallfølger og rekker. Side 4.
Så går vi løs på det mer generelle Taylor-polynomet i kap. 4.3 (4.2). Se definisjon 4.2 og eks.
4.4, og løs oppgave 4.4.
I kap. 4.4 (4.3) lar vi antall ledd gå mot uendelig, slik at vi får rekker. De nødvendige
definisjoner finner du i definisjon 4.3 og 4.4. Det grunnleggende resultatet finner du i setning
4.1. Denne setningen kan virke litt kronglete, men hovedinnholdet er at dersom Taylor-rekka
fra definisjon 4.3 konvergerer, så vil den konvergere mot fbxg
. Restledd-formelen angir en
øvre grense for den feilen vi gjør ved å kutte rekka etter n ledd.
Gå gjennom eks. 4.7 (4.6) og 4.8 (4.7).
Vi har nå utledet de tre viktigste Taylor-rekkene (egentlig Maclaurin-rekker):
3 5 7
x x x
sin x = x− + − +
3! 5! 7!
2 4 6
x x x
cos x = 1− + − +
2! 4!
6!
2 3 4
x x x
e
x = 1 + x + 2! + 3! + 4!
+
Disse rekkene danner utgangspunkt for mange andre rekker. Du bør derfor kjenne til dem. Se
eks. 4.9 (4.8) og 4.10 (4.9). Se også setning 4.2, og eks. 4.11 (4.10) og 4.13 (4.12).
Oppgave 4.6 a,b,c, 4.8, 4.9. (Hint til 4.9a: Tenk geometrisk rekke. Hint til 4.9b: Erstatt
x med x 2 ).
b g med konvergensområde − < <
I eks. 4.14 (4.13) utledes ei Taylor-rekke for ln 1+ x
1 x 1.
Også denne rekka bør du innlemme i formelsamlingen sammen med rekkene for sin x , cos x
og e x . I eks. 4.15 (4.14) utledes ei Taylor-rekke for ln x om x = 2 . Sammenlikn med din
løsning av oppgave 4.4.
Oppgave 4.7a,b.
b
Du kjenner kanskje binomialformelen for 1+ x m
når m er et helt, positivt tall. I kap. 4.4
generaliseres denne formelen slik at den også kan brukes for andre verdier av m. Se hvordan
formelen brukes i eks. 4.16 (4.15) og i eks. 4.17 (4.16).
Oppgave 4.11.
Et råd til slutt: Dersom du skal sette opp Taylor-rekka til en funksjon f x , bør du ikke gyve
løs på definisjon 4.3 med det samme. Undersøk om rekka kan settes opp på grunnlag av
x
allerede kjente rekker, f.eks. rekkene for sin x , cos x , e og ln x . Undersøk også om f x
a
kan omformes til (eller inneholder en slik faktor), slik at du kan sette opp ei geometrisk
1− k
rekke. Se f.eks. oppgave 4.9a. Dette er jo summen av den uendelige geometriske rekka
2
a+ ak + ak + . Brøkfunksjoner og funksjoner som inneholder rotuttrykk kan ofte
behandles med formelen for binomisk rekke (kap. 4.4).
Vi tar ikke med kap. 4.6 og 4.7 (4.5) om løsing av differensiallikninger.
g
b g
b g
Bjørn Davidsen, Universitetet i Tromsø. 2009.