8. Krumning og krumningsradius. - Universitetet i Tromsø

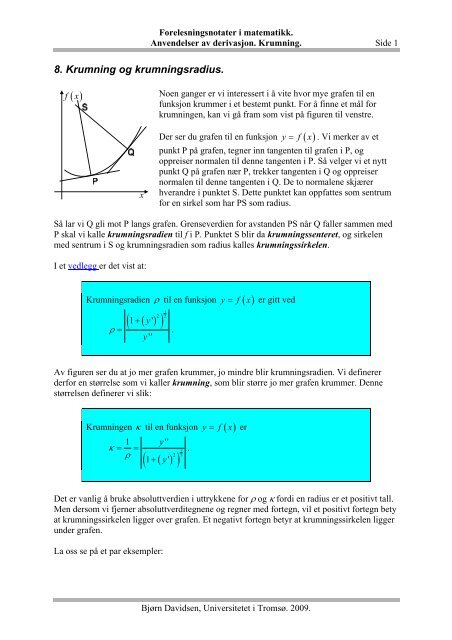
Forelesningsnotater i matematikk.Anvendelser av derivasjon. Krumning. Side 18. Krumning og krumningsradius.f( x)Noen ganger er vi interessert i å vite hvor mye grafen til enfunksjon krummer i et bestemt punkt. For å finne et mål forkrumningen, kan vi gå fram som vist på figuren til venstre.xDer ser du grafen til en funksjon y = f ( x). Vi merker av etpunkt P på grafen, tegner inn tangenten til grafen i P, ogoppreiser normalen til denne tangenten i P. Så velger vi et nyttpunkt Q på grafen nær P, trekker tangenten i Q og oppreisernormalen til denne tangenten i Q. De to normalene skjærerhverandre i punktet S. Dette punktet kan oppfattes som sentrumfor en sirkel som har PS som radius.Så lar vi Q gli mot P langs grafen. Grenseverdien for avstanden PS når Q faller sammen medP skal vi kalle krumningsradien til f i P. Punktet S blir da krumningssenteret, og sirkelenmed sentrum i S og krumningsradien som radius kalles krumningssirkelen.I et vedlegg er det vist at:Krumningsradien ρ til en funksjon y = f ( x)er gitt ved2( 1 + ( y '))32ρ = .y ''Av figuren ser du at jo mer grafen krummer, jo mindre blir krumningsradien. Vi definererderfor en størrelse som vi kaller krumning, som blir større jo mer grafen krummer. Dennestørrelsen definerer vi slik:Krumningen κ til en funksjon y = f ( x)er1 y ''κ = =ρ2( 1 + ( y') )23.Det er vanlig å bruke absoluttverdien i uttrykkene for ρ og κ fordi en radius er et positivt tall.Men dersom vi fjerner absoluttverditegnene og regner med fortegn, vil et positivt fortegn betyat krumningssirkelen ligger over grafen. Et negativt fortegn betyr at krumningssirkelen liggerunder grafen.La oss se på et par eksempler:Bjørn Davidsen, Universitetet i Tromsø. 2009.

Forelesningsnotater i matematikk.Anvendelser av derivasjon. Krumning. Side 2Eksempel 8.1: Finn krumningsradien til disse funksjonene:a) y = f x = x i punktet ( 0, 0).2( )= ( ) = ln( 1, 0)b) y f x x i punktet .Løsning:a)2y = x ⇒ y' = 2 x ⇒ y'' = 2.( 1 + ( y' ) ) 1+( 2x)( )3 32 2 2 2ρ = = .y '' 2Setter inn x = 0 og får( + ) 3 21 0 1ρ = = .2 22Grafen til y = x er vist til høyresammen med krumningssirkelen.y 1.00.80.60.40.2-1.0 -0.8 -0.6 -0.4 -0.2 0.0 0.2 0.4 0.6 0.8 1.0xb)y = ln x ⇒ y'= = x1x⇒ y''=− x =−−2 12x−1Istedenfor å sette inn disse uttrykkene i formelenfor ρ, er det lettere å beregne verdiene av y ' ogy '' i punktet ( 1, 0)før innsettingen:Da får viy ' = = = 1.1 1x 11 12 2x 1y '' =− =− =− 1.32 22( 1 + ( y ')) ( 1+1 )ρ = =y '' −1323( )12= 2 = 2 = 8 = 2 232y101 2 3 4 5-1-2-3-4Grafen til y = ln x sammen medkrumningssirkelen.xMerk at dersom vi regner med fortegn, vil ρ bli positiv i eksempel a) og negativ i eksempelb). Dette stemmer med at krumningssirkelen ligger over grafen til f dersom ρ > 0 og undergrafen til f dersom ρ < 0.Oppgave 8.1.Bjørn Davidsen, Universitetet i Tromsø. 2009.