Responder às solicitações da professora, tomando nota de tudo o ...

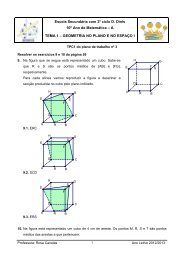
Escola Secundária com 3º ciclo D. Dinis
10º Ano de Matemática – A
Módulo Inicial
Aula 1 do plano de trabalho nº1
Sumário: Sólidos geométricos; Porque é que há só 5 sólidos platónicos?
Começámos por distinguir um sólido de uma sua representação. O sólido é maciço e a sua
representação pode ser oca ou ter só as arestas e os vértices, simulando as faces.
Sólido Geométrico é uma porção fechada do espaço, limitado por superfícies planas ou curvas.
Em seguida definimos poliedro – é um sólido limitado apenas por superfícies planas (polígonos).
Como exemplos de não poliedros vimos alguns sólidos de revolução – cilindro, cone e esfera.
Chamam-se sólidos de revolução por resultarem da rotação de uma figura plana em torno de um
eixo de simetria (rectângulo, triângulo ou círculo, respectivamente).
Os poliedros podem ser côncavos ou convexos.
Poliedro convexo – sólido de faces planas que contém todos os segmentos de recta que têm
como extremos dois quaisquer dos pontos do sólido, ou que não é intersectado pelo plano de
suporte de qualquer uma das suas faces.
Poliedro convexo
Poliedro côncavo
Poliedro côncavo quando o plano, que contém alguma das suas faces, divide o poliedro em duas
partes.
Os poliedros podem ser irregulares ou regulares.
Professora: Rosa Canelas 1
Ano Lectivo 2009/2010

Como exemplos de poliedros irregulares vimos:
Pirâmides
Prismas
Antiprisma
Bipirâmides
Vimos cinco poliedros convexos regulares que são regulares porque todas as faces são
polígonos regulares geometricamente iguais, todas as arestas são geometricamente iguais e em
todos os vértices convergem o mesmo número de faces ou arestas.
Tentámos provar que apenas há 5 poliedros convexos regulares (sólidos platónicos) e para
isso partimos de polígonos regulares, triângulos equiláteros, quadrados, pentágonos e
hexágonos que poderiam ser faces de um poliedro convexo regular.
Face possível
para o
poliedro
regular
Triângulo
equilátero
Nº de
faces
por
vértice
Esboço plano das
faces concorrentes em
cada vértice
Amplitude
de um
ângulo
interno de
cada face
Soma das amplitudes
dos ângulos internos
em torno do mesmo
vértice
Nome do
poliedro
regular
3 60º 180º Tetraedro
Triângulo
equilátero
4 60º 240º Octaedro
Professora: Rosa Canelas 2
Ano Lectivo 2009/2010

Triângulo
equilátero
5 60º 300º Icosaedro
Triângulo
equilátero
6 (ou
mais)
60º 360º
Não há
poliedro
Quadrado 3 90º 270º cubo
Quadrado
4 (ou
mais)
90º 360º
Não há
poliedro
Pentágono 3 108º 324º Dodecaedro
Pentágono 4 108º 432º
Não há
poliedro
Hexágono
3 (ou
mais)
120º 360º
Não há
poliedro
Foi preciso fazer umas contas para saber a medida do ângulo interno do pentágono regular.
Inscrevemo-lo numa circunferência e concluímos que:
• O ângulo interno do pentágono é inscrito na circunferência e a sua amplitude é metade da
amplitude do arco compreendido entre os seus lados.
• Concluímos que:
Professora: Rosa Canelas 3
Ano Lectivo 2009/2010

o
o
o
O pentágono divide a circunferência em 5 partes iguais, cada arco mede
360º
72º
5 =
O arco compreendido entre os lados do ângulo
interno é o igual a três vezes 72º ou seja 216º.
A medida do ângulo interno é portanto metade
de 216º ou seja 108º.
360
= 72
5
72⋅3
= 108
2
Finalmente concluímos que só há 5 sólidos platónicos:
72 x 3
2
Estudámos cada um dos sólidos platónicos relativamente ao tipo e número de faces, número de
vértices e número de arestas e planificação. O nome de cada poliedro está relacionado com o
número de faces.
POLIEDROS FACES Nº de faces Nº de vértices Nº de arestas Planificação
TETRAEDRO Triângulo 4 4 6
CUBO ou
HEXAEDRO
Quadrado 6 8 12
OCTAEDRO Triângulo 8 6 12
Professora: Rosa Canelas 4
Ano Lectivo 2009/2010

POLIEDROS FACES Nº de faces Nº de vértices Nº de arestas Planificação
DODECAEDRO Pentágono 12 20 30
ICOSAEDRO Triângulo 20 12 30
Professora: Rosa Canelas 5
Ano Lectivo 2009/2010