actividade 4 da página 59 e a actividade 7 da página 69

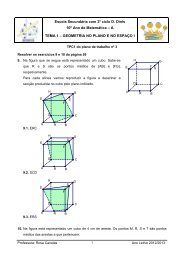
Escola Secundária com 3º ciclo D. Dinis10º Ano de Matemática – AGeometria no Plano e no Espaço IAula 4 do plano de trabalho nº 3Resolver a actividade 4 da página 59 e a actividade 7 da página 69Actividade 4Composição e decomposição de sólidosNa figura estão representados dois recipientes, A e B, obtidos a partir de cubos. Sabe-se queambos os cubos têm igual aresta e que para encher o recipiente A são precisos 30 copos deágua.1. Pretendemos saber quantos copos de água são necessários para encher a cavidade dorecipiente B. Sabemos que o vértice da pirâmide coincide com o centro do cubo e temos comosugestão: “Observar a seguinte sequência de imagens”:Observando cuidadosamente a sequência de imagens verificamos que o cubo se podedecompor em seis pirâmides quadrangulares regulares com base igual à face do cubo e comaltura igual a metade da aresta do cubo. Então o volume da pirâmide é a sexta parte dovolume do cubo e a cavidade do recipiente B fica cheia com 1 × 30 = 5 copos de água.62. Vamos confirmar a resposta anterior designado por a a aresta do cubo.Professora: Rosa Canelas 1Ano Lectivo 2009/2010

O volume do cubo éVcubo3= a e o volume de uma pirâmide é:31 a a1= × × ⇔ = ou seja Vpirâmide = × Vcubopelo que a cavidade do recipiente3 2 662Vpirâmidea VpirâmideB fica cheia com 5 copos porque 1 30 56 × = .3. Juntando à sequência de imagens apresentadas em 1. juntamos a imagem IV e pretendemossaber qual a razão entre os volumes dos sólidos apresentados em IV e em I.Sendo que a figura IV é obtida por juntar à imagem I (cubo) as seis pirâmides da figura IIIobtemos um sólido com o dobro do volume do cubo.VIVI2V = Actividade 7Na figura, está representado o cuboctaedro, sólido que se obtém a partir do cubo, truncando-o porplanos definidos por pontos médios das suas arestas, e a respectiva planificação.Professora: Rosa Canelas 2Ano Lectivo 2009/2010

1. Pretendemos saber qual a relação que existe entre a aresta do cuboctaedro e a do cubo quelhe deu origem. Pensemos no que acontece numa das faces do cubo que lhe dá origem:a2xa2aSe a representa a aresta do cubo e x a aresta do cuboctaedropodemos obter, por aplicação do Teorema de Pitágoras:2 2 2 2 22 ⎛ ⎞ ⎛ ⎞ 2a a a a 2a 2x = ⎜ ⎟ + ⎜ ⎟ ⇔ x = + ⇔ x = ⇔ x = a⎝ 2 ⎠ ⎝ 2 ⎠ 4 4 4 2A relação entre as arestas dos dois sólidos é2. Consideremos que o cubo original tem 18 cm de aresta.2.1. Pretendemos determinar a área de cada um dos sólidos.Comecemos pela área do cubo:• Aresta do cubo a = 18x =2a2• Área da face do cuboA = 18 ⇔ A = 324cmface2 2face• Área total do cubo que tem 6 faces iguais:A = 6 × 324 ⇔ A = 1944cmcubocubo2Calculemos agora a área do cuboctaedro:• Aresta do cuboctaedro2x = × 18 ⇔ x = 9 2 cm2• Área duma face quadrada:( ) 2 2A = 9 2 ⇔ A = 81× 2 ⇔ A = 162cmface quadrada face quadrada face quadradaPara calcularmos a área de uma face triangular precisamos de calcular a altura dotriângulo equilátero de lado igual à aresta do cuboctaedro:222 2⎛ ⎞• Altura do triângulo: ⎜ ⎟ ( )2 81 243 3h = 162 − ⇔ h = ⇔ h = 92 2 29 2 81h + = 9 2 ⇔ h + = 162 ⇔⎜ 2 ⎟⎝ ⎠2• Área do triângulo:39 2 × 92 81 3A = ⇔ A =2 2h9 29 22Professora: Rosa Canelas 3Ano Lectivo 2009/2010

• Área do cuboctaedro que tem 6 faces quadradas e 8 triangulares:( )281 3Acuboctaedro= 6 × 162 + 8 × ⇔ Acuboctaedro= 972 + 324 3 cm22.2. Calculemos o volume do cuboctaedro recorrendo à sugestão: ”Partindo do cubo, recorrerà decomposição de sólidos”Precisamos de pensar como se obteve o cuboctaedro a partir docubo. Na figura que representa um cuboctaedro e o cubo de quederiva é fácil ver que foram retiradas, ao cubo, 8 pirâmides iguais àpirâmide [ ABCD ] .Vamos então calcular:• O volume do cubo3 3V = 18 ⇔ V = 5832cmDACB1 9 × 9 243• O volume de cada pirâmide Vpirâmide = × × 9 ⇔ Vpirâmide=3 2 2• Volume do cuboctaedro243Vcuboctaedro= 5832 − 8 × ⇔ Vcuboctaedro= 4860cm233. Partindo de um cubo qualquer de aresta a, vamos estabelecer uma relação entre os volumesdo cubo e do cuboctaedro que dele resulta.Vamos então calcular:• O volume do cuboV = a3• O volume de cada pirâmidea a×2 31 a 1 a a aV 2 2pirâmide= × × ⇔ Vpirâmide = × × ⇔ Vpirâmide=3 2 2 3 8 2 48• Volume do cuboctaedroV a 8 a V a a V 5 a48 6 63 33 3 3cuboctaedro= − × ⇔cuboctaedro= − ⇔cuboctaedro=4. Determinemos a capacidade de um frasco de perfume com a forma de umcuboctaedro com 4 cm de aresta. Pretende-se o resultado em mililitros,arredondado às unidades e com o raciocínio explicado.Já sabemos a relação entre a aresta do cubo e a do cuboctaedro2x = a , sabendo nós que x = 4 podemos:2• Obter a aresta do cubo que dá origem ao cuboctaedro:Professora: Rosa Canelas 4Ano Lectivo 2009/2010

2 8 8 24 = a ⇔ a = ⇔ a = ⇔ a = 4 22 2 2• Calcular o volume desse cubo: ( ) 3V = 4 2 ⇔ V = 64 × 2 2 ⇔ V = 128 2cubo cubo cubo• Calcular o volume do cuboctaedro:5 320 2Vcuboctaedro= × 128 2 ⇔ Vcuboctaedro= cm6 33Em mililitros com aproximação às unidades o volume do cuboctaedro é 150 ml.(aproximação àsunidades, por defeito)Professora: Rosa Canelas 5Ano Lectivo 2009/2010