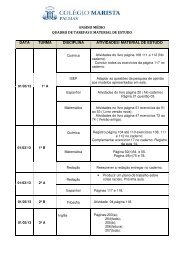
Apresentação do PowerPoint

FRAÇÕES DE UMA QUANTIDADE

FRAÇÕES DE UMA QUANTIDADEPREPARANDO O BOLODICASHelena comprou 24 ovos. Ela precisa de 2 6 dessaquantidade para fazer o bolo de aniversário de Mariana.De quantos ovos Helena vai precisar?Faça desenhos no seu caderno. Eles o ajudarão aresponder a pergunta.O numerador representa quantas partes foramutilizadas.O denominador representa o total de partes que ointeiro foi dividido.

FRAÇÕES DE UMA QUANTIDADEPREPARANDO OBOLOHelena comprou 24 ovos. Ela precisa de 2 6dessa quantidade para fazer o bolo de aniversáriode Mariana. De quantos ovos Helena vai precisar?24 ovosPROCESSO PRÁTICO26de 24 =?24 ÷ 6 = 44 × 2 = 81616de 24 = 8 ovos. 26Helena vaiprecisar de 8ovos16161616

FRAÇÕES DE UMA QUANTIDADEDICASAMIGOS CONVIDADOSFaça desenhos no seu caderno. Eles o ajudarão aresponder a pergunta.O numerador representa quantas partes foramutilizadas.O denominador representa o total de partes que ointeiro foi dividido.Dos amigos que Mariana convidou para a festa, 20estudam na mesma classe que ela, o que corresponde a5do número de convidados. Quantas pessoas Mariana6convidou para a festa?

FRAÇÕES DE UMA QUANTIDADEAMIGOSCONVIDADOSDos amigos que Mariana convidou para a festa, 20 estudam na mesma classe que ela, o quecorresponde a 5 6do número de convidados. Quantas pessoas Mariana convidou para a festa?56corresponde a 20 amigos

FRAÇÕES DE UMA QUANTIDADEAMIGOSCONVIDADOSDos amigos que Mariana convidou para a festa, 20 estudam na mesma classe que ela, o quecorresponde a 5 6do número de convidados. Quantas pessoas Mariana convidou para a festa?PROCESSO PRÁTICO56de ? = 20Mariana convidou24 amigos.20 ÷ 5 = 44 × 6 = 2416corresponde a20 ÷ 5 = 46corresponde a66 × 4 = 24.

FRAÇÕES DE UMA QUANTIDADEATIVIDADE 01 ATIVIDADE 02Resolva as questões: 28 a 31.Página: 142Resolva as questões: 32 a 40.Páginas: 143 a 145Caso não termine a atividade, em sala, a mesma fica como tarefa para a próxima aula.

FRAÇÕES EQUIVALENTESEquivalenteigualvalorFrações que representam a mesma parte do inteiro são chamadas frações equivalentes.1224

FRAÇÕES EQUIVALENTES1º CASO 2º CASO343668249121234 = 6 8 = 912frações equivalentes36 = 2 4 = 1 2frações equivalentes

FRAÇÕES EQUIVALENTESUMA PROPRIEDADE IMPORTANTEQuando multiplicamos ou dividimos o numerador e o denominador de uma fração pelo mesmo número, diferente dezero, obtemos sempre uma fração equivalente à fração dada.× 2× 3÷ 3÷ 233324 = 6 84 = 9 126 = 1 24 = 1 2× 2× 3÷ 3÷ 2

SIMPLIFICAÇÃO DE FRAÇÕESPara simplificar uma fração, devemos dividir o numerador e o denominador da fração dada por um MESMO NÚMEROmaior que 1.÷ 2÷ 2÷ 3122436 = 1218 = 6 9 = 2 3ou2436 = 2 3÷ 2÷ 2÷ 3÷ 12A fração 2 3é chamada de fração irredutível.÷

OPERAÇÕES COM FRAÇÕES

OPERAÇÕES COM FRAÇÕESADIÇÃO E SUBTRAÇÃO DE FRAÇÕES COMDENOMINADORES IGUAISUm ciclista deve percorrer uma pista de corrida em três etapas. Primeiro ele deverá percorrer 3/10 do total. No segundopercurso ele deverá pedalar mais 5/10 da pista. Quanto faltará para percorrer o restante?INÍCIOCHEGADA310510210

OPERAÇÕES COM FRAÇÕESADIÇÃO E SUBTRAÇÃO DE FRAÇÕES COMDENOMINADORES IGUAISPara adicionarmos frações de mesmo denominador, somamos os numeradores e conservamos o denominador.251535

OPERAÇÕES COM FRAÇÕESADIÇÃO E SUBTRAÇÃO DE FRAÇÕES COMDENOMINADORES DIFERENTESPara somar ou subtrair frações que tem denominadores diferentes, reduzimos as frações ao mesmo denominador eprocedemos como no caso anterior.fração equivalente35 + 1 2 = 6 10 + 5 10 = 1110fração equivalente

OPERAÇÕES COM FRAÇÕESADIÇÃO E SUBTRAÇÃO DE FRAÇÕES COMDENOMINADORES DIFERENTESLembre - se que você pode encontrar um denominador comum descobrindo o MÍNIMO MULTIPLO COMUMDESSES NÚMEROS.Exemplos: Efetue as operações.a)b)c)2+ 7 3 87− 2 3 52+ 1 3 2

OPERAÇÕES COM FRAÇÕESMULTIPLICAÇÃO DE FRAÇÕESNÚMERO NATURAL VEZES FRAÇÃOGabriela tem uma fita com 2/5 de metro de comprimento. Para um trabalho escolar, ela precisará de 3 fitas iguais a essa. Quantosmetros de fita ela vai usar nesse trabalho?Aqui basta usar a ideia de multiplicação relacionada à adição de parcelas iguais:3 × 2 5 = 2 5 + 2 5 + 2 5 = 6 5 , ou seja, 3 × 2 5 = 6 5Multiplicamos o número natural pelo numerador e conservamos o denominador.

OPERAÇÕES COM FRAÇÕESMULTIPLICAÇÃO DE FRAÇÕESFRAÇÃO VEZES FRAÇÃO01. Numa empresa, 1/3 dos funcionários são mulheres. Entre as mulheres, ½ delas são casadas. A quantidade de mulheres casadasrepresenta que fração do número de funcionários dessa empresa?Essa problema pode ser traduzido assim:Quanto dá 1 2 de 2 3 ?Em matemática, a palavra “de” pode sersubstituida pelo sinal × de multiplicação.

OPERAÇÕES COM FRAÇÕESMULTIPLICAÇÃO DE FRAÇÕESFRAÇÃO VEZES FRAÇÃOResolvendo a situação geometricamente:A parte roxa representa 1/6 da figura.Deste modo podemos concluir que:1/3 são mulheres.12 de 1 3 (casadas)12 de 1 3 → 1 2 × 1 3 = 1 6 → 1 × 12 × 3 = 1 6Para calcular o produto de duas frações multiplicamos osnumeradores entre si e os denominadores entre si.

OPERAÇÕES COM FRAÇÕESMULTIPLICAÇÃO FRAÇÕESFRAÇÃO VEZES FRAÇÃO02. Em uma sala de aula, 2/3 dos alunos praticam esportes. Desses alunos, 3/4 jogam voleibol. Que fração dos alunos da sala praticavoleibol?Quanto dá 3 4 de 2 3 ?praticamesportes23praticamvoleibol34 × 2 3 = 3 × 24 × 3 = 612A fração que representa os alunos que praticamvoleibol é ½.Não esqueça desimplificar.

OPERAÇÕES COM FRAÇÕESMULTIPLICAÇÃO DE FRAÇÕESNÚMERO NATURAL VEZES FRAÇÃOFRAÇÃO VEZES FRAÇÃOMultiplicamos o número natural pelo numerador da fração e Para calcular o produto de duas frações multiplicamos osconservamos o denominador.numeradores entre se e os denominadores entre si.26 ∙13 =35 ∙ 4 7 =35 ∙20 = 13 ∙ 5 9 =Não esqueça desimplificar.Tarefa:Atividades: 71 a 81.

OPERAÇÕES COM FRAÇÕESINVERSA DE UMA FRAÇÃOINVERSA DE UMAFRAÇÃOQuando o produto deduas frações é igual a 1,essas frações são inversasuma da outra.35Será 3 5 a inversa de 5 3 ?35 ∙ 5 3 = 1515 = 153É só virár de ponta a cabeça.

OPERAÇÕES COM FRAÇÕESDIVISÃO DE FRAÇÕESDIVISÃO DE UMNÚMERO NATURALPOR FRAÇÃONo garrafão há 3 litros de água.01. Quantas garrafas de 1 litro posso encher? 02. Quantas garrafas de 1/2 litro posso encher?Observe esses exemplos:12 l12 l12 l3l1l1l1l3l12 l12 l12 l

OPERAÇÕES COM FRAÇÕESDIVISÃO DE FRAÇÕESDIVISÃO DE UMNÚMERO NATURALPOR FRAÇÃONo garrafão há 3 litrosde água Quantos coposde ¼ de litro possoencher?3lPara saber quantas vezes uma quantidade cabe em outra, usamos a divisão:14 l 14 l 14 l 14 l14 l 14 l 14 l 14 l14 l 14 l 14 l 14 l3 ÷ 1 4 =? Esse resultado é o mesmo que seobtêm quando multiplicamos 3 peloinverso de ¼.3 ÷ 1 4 =? → 3 ∙ 4 1 = 12inverte

OPERAÇÕES COM FRAÇÕESDIVISÃO DE FRAÇÕESDIVISÃO DE FRAÇÃOPara dividir uma fração por outra, basta multiplicar a primeira pelo inverso da segunda.POR FRAÇÃO57 ÷ 2 3 =? → 57 ∙ 3 2 = 1514a) 7 9 ÷ 4 5 = b) 4 5 ÷ 2 inverte3 = b) 1 5 ÷ 7 2 =Tarefa:Atividades: 82 a 92.