escola secundária com 3º ciclo d. dinis 10º ano de matemática

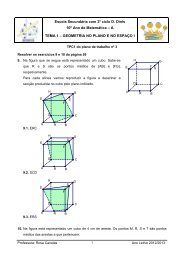
ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS10º ANO DE MATEMÁTICA – A09 - 03 - 2007Teste de avaliação(Versão A)Grupo I• As cinco questões deste grupo são de escolha múltipla.• Para cada uma delas são indicadas quatro alternativas, das quais só uma está correcta.• Escreva na sua folha de respostas a letra correspondente à alternativa que seleccionar para cada questão.• Se apresentar mais do que uma resposta, a questão será anulada, o mesmo acontecendo se a letra transcritafor ilegível.• Não apresente cálculos ou justificações.• Cada resposta certa vale 9 pontos, cada pergunta não respondida, anulada ou com resposta errada vale 0(zero) pontos.1. A secção produzida pelo plano que passa nos pontos M, N e G(M e N são pontos médios das arestas a que pertencem) é(A) Um triângulo equilátero(B) Um paralelogramo(C) Um trapézio(D) Um triângulo rectângulo.2. De um triângulo equilátero sabemos que o lado mede 4.Podemos afirmar que a sua área mede:(A) 6(B) 4 3(C) 3(D) 2 6.3. Num referencial o.n. ( O, x, y ) a recta vertical que passa no ponto de coordenadas ( 2, − 3)tem equação:(A) x =− 3(B) y = 2(C) x = 2(D) y = −34. Considere, num referencial o.n. Oxyz:2 2 2- a esfera E definida pela condição ( ) ( ) ( )- a recta r de equação ( x, y,z) = ( 1,2,3 ) + k ( −2,0,1 ),k∈x− 1 + y− 2 + z−3 ≤ 36PROFESSORA: Rosa Canelas 12006/2007

A intersecção da recta r com a esfera E é um segmento de recta.O comprimento desse segmento de recta é:(A) 8(C) 12(B) 10(D) 14. 5. Supondo que XY = PQ . Indique qual das afirmações seguintes é necessariamente verdadeira(A) XY ⊥ PQ (B) XQ = PY(C) XQ⊥ PY(D) [ XYQP ] é um paralelogramoGrupo IINas questões deste grupo apresente o seu raciocínio de forma clara, indicando todosos cálculos ou esquemas que tiver de efectuar e todas as justificações necessárias.Atenção: quando não é indicada a aproximação que se pede para um resultado,pretende-se sempre o valor exacto.1. O gráfico da figura representa avariação da temperatura numdeterminado local ao longo de umperíodo de 48 horas.1.1. Que variáveis estão relacionadasatravés deste gráfico? Qual é avariável independente e qual é avariável dependente?1.2. Justifique que a relação entre asvariáveis representada pelo gráfico é uma função.1.3. Indique o domínio e o contradomínio da função.1.4. Qual foi a temperatura máxima em cada dia e a que horas se fez sentir essatemperatura em cada dia?1.5. Construa uma tabela de monotonia e extremos desta função.1.6. A que horas foi nula a temperatura em cada dia?1.7. Construa uma tabela de variação de sinal da função.PROFESSORA: Rosa Canelas 22006/2007

2. Considere o referencial xOy da figura. Nele os pontos A e C pertencem à recta s e A pertenceà circunferência de centro C.2.1. Indique uma equação cartesiana que sirva paradefinir o eixo Ox.2.2. Escreva uma equação vectorial que sirva paradefinir o eixo Oy.2.3. Mostre que a equação reduzida da recta s é1 1y = x+ .2 221OyAC-1 1 2 3 4 5sx2.4. Determine as coordenadas do ponto simétrico de A em relação ao ponto C.2.5. Calcule, na forma mais simplificada possível, a equação da mediatriz do segmento [AC].2.6. Represente analiticamente o conjunto de pontos a sombreado na figura, incluindo a fronteira.3. Na figura está representada, em referencial o.n. Oxyz, uma pirâmide quadrangular regular.A base da pirâmide está contida no plano de equação z = 4.O vértice A pertence ao eixo OzO vértice B pertence ao plano yOzO vértice D pertence ao plano xOzO vértice C tem coordenadas ( 4, 4, 4 )A altura da pirâmide é 6.3.1. Indique as coordenadas dos pontos A, B, D e E.3.2. Escreva uma equação vectorial da recta CE3.3. Determine a área da secção produzida na pirâmide peloplano xOyPROFESSORA: Rosa Canelas 32006/2007

COTAÇÕESGrupo I ........................................................................................................ 45Cada resposta certa.......................................................................... 9Cada questão não respondida ou anulada....................................... 0Grupo II ........................................................................................................ 1551. ............................................................................................................................... 701.1 ...............................................................………………............... 101.2 ………………………………………………………………………… 101.3 ………………………………………………………………………… 101.4 ………………………………………………………………………… 101.5 ………………………………………………………………………… 101.6 ………………………………………………………………………… 101.7 ………………………………………………………………………… 102. ................................................................................................................………… 452.1 ...............................................................………………………… 52.2 ...............................................................…………………………. 52.3 ...............................................................…………………………. 102.4 ………………………………………………………………………… 52.5 ………………………………………………………………………… 102.6 ………………………………………………………………………… 103. ........................................................................................................ …….............. 403.1 ...............................................................………………………… 123.2 ...............................................................…………………………. 103.3 ...............................................................…………………………. 18TOTAL ........................................................................................................ 200PROFESSORA: Rosa Canelas 42006/2007

ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS10º ANO DE MATEMÁTICA – A09 - 03 - 2007Teste de avaliação – proposta de resolução(Versão A)Grupo I1. (C) A secção produzida pelo plano que passa nos pontos M, Ne G (M e N são pontos médios das arestas a que pertencem)é o trapézio isósceles [MNGD].AEMBNF2. (B) De um triângulo equilátero sabemos que o lado mede 4.Podemos afirmar que a sua área mede 4 3 , porque da figuraDHCGresulta por aplicação do Teorema de Pitágoras que2 2 2 2h + 2 = 4 ⇔ h = 12⇔ h= 2 3 e por aplicação da fórmulaque dá a área de um triângulo resulta queh44×2 3A = ⇔ A = 4 3223. (C) Num referencial o.n. ( O,x,y ) a recta vertical que passa no ponto de coordenadas ( 2, − 3)tem equação x = 2 porque se a recta é vertical todos os pontos têm a mesma abcissa.4. (C) Considere, num referencial o.n. Oxyz:2 2 2- a esfera E definida pela condição ( x− 1) + ( y− 2) + ( z−3)≤ 36- a recta r de equação ( x, y,z) = ( 1,2,3 ) + k ( −2,0,1 ),k∈A intersecção da recta r com a esfera E é um segmento de recta.O comprimento desse segmento de recta é 12 porque a recta passa no centro da esferaintersectando-a segundo um segmento de comprimento igual aodiâmetro da esfera, que tendo raio 6 tem diâmetro 12.Y 5. (D) Supondo que XY = PQ . A afirmação que é necessariamenteverdadeira é [ XYQP ] é um paralelogramo.XQPPROFESSORA: Rosa Canelas 52006/2007

Grupo II1. O gráfico da figura representa avariação da temperatura numdeterminado local ao longo de umperíodo de 48 horas.1.1. As variáveis relacionadas são otempo e a temperatura, sendo aprimeira a independente e asegunda a dependente.1.2. A relação entre as variáveisrepresentada pelo gráfico é uma função porque a cada valor do tempo corresponde ume um só valor para a temperatura.1.3. O domínio desta função é o conjunto D = [0,48]. O contradomínio é o conjuntoD' = [ − 3,11].1.4. A temperatura máxima no primeiro dia é 8ºC atingida às 14 horas e no segundo dia é11ºC atingida também às 14 h do segundo dia.1.5. Uma tabela de monotonia e extremos desta função é:t (h) 0 4 14 26 38 48temp (ºC) -1 -3 8 -3 11 -3MmMmMm1.6. A temperatura foi nula às 8 h e às 20 h do 1º dia e às 8 h e às 22h do segundo dia.1.7. Uma tabela de variação de sinal da função é:t (h) 0 8 20 32 46 48temp (ºC) -1 - 0 + 0 - 0 + 0 - -32. Consideremos o referencial xOy da figura. Nele os pontos A e C pertencem à recta s e Apertence à circunferência de centro C.2.1. Uma equação cartesiana que sirva para definiro eixo Ox é y = 0ys2.2. Uma equação vectorial que sirva para definir oeixo Oy é ( x, y) = ( 0,0 ) + k ( 0,1 ), k ∈21ACO-1 1 2 3 4 5xPROFESSORA: Rosa Canelas 62006/2007

2.3. A equação reduzida da recta s é1 1y = x+ , porque:2 2• a recta s passa nos pontos A(1,1) e C(3,2)• Dos dois pontos podemos definir o vector AC de coordenadasAC = C − A = 3,2 − 1,1 = 2,1( ) ( ) ( )e concluir que o declive é 1 2 .1• Substituindo na equação y = x+ b as coordenadas x e y pela abcissa e pela2ordenada de um dos pontos da recta podemos concluir que1 1 11= × 1+ b⇔ b= 1− ⇔ b= .2 2 2• Finalmente como já sabemos o declive e a ordenada na origem podemos escrever1 1a equação da recta y = x+ como queríamos demonstrar.2 22.4. As coordenadas do ponto simétrico de A em relação ao ponto C são (5,3) e obtêm-seC+ AC = (3,2) + (2,1) = 5,3 .calculando ( )2.5. Calculemos, na forma mais simplificada possível, a equação da mediatriz do segmento[AC].( ) ( ) ( ) ( )2 2 2 2 2 2 2 2x− 1 + y− 1 = x− 3 + y−2 ⇔ x − 2x+ 1+ y − 2y+ 1= x − 6x+ 9+ y − 4y+ 4⇔114x + 2y = 11⇔ 2y = − 4x + 11⇔ y = − 2x +22.6. Representemos analiticamente o conjunto de pontos a sombreado na figura, incluindoa fronteira.• Comecemos por identificar as fronteiras:o Eixo Ox com equação y = 0o Eixo Oy com equação x = 0oRecta s com equação1 1y = x+2 2o Circunferência com centro em C e que passa em A e que por isso tem raio2 2igual a AC = 2 + 1 = 5. A equação da circunferência é( ) ( )2 2x− 3 + y− 2 = 5.• O conjunto de pontos que queremos definir estão acima do eixo Ox, à direita do eixoOy, abaixo da recta s e fora da circunferência de centro C e raio5 e por isso1 12 2y ≥0∧x ≥0∧y ≤ x+ ∧ x− 3 + y−2 ≥ 52 2define-se pela condição: ( ) ( )PROFESSORA: Rosa Canelas 72006/2007

3. Na figura está representada, em referencial o.n. Oxyz, uma pirâmide quadrangularregular.A base da pirâmide está contida no plano de equação z = 4 .O vértice A pertence ao eixo OzO vértice B pertence ao plano yOzO vértice D pertence ao plano xOzO vértice C tem coordenadas ( 4, 4, 4 )A altura da pirâmide é 6.3.1. As coordenadas dos pontos A, B, D e E. são:A ( 0,0, 4 ), B( 0,4,4 ) , D( 4,0,4 ) e E( 2,2, − 2)3.2. Para escrevermos uma equação vectorial da rectaCE vamos começar por calcular as coordenadas dovector CE .• CE = E − C = ( 2,2, −2) − ( 4, 4, 4) = ( −2, −2, −6)Podemos agora escrever uma equação vectorial de CE( x, y,z) = ( 4,4,4 ) + k ( −2, −2, −6 ),k∈3.3. Determinemos a área da secção produzida na pirâmide pelo plano xOy.• A secção é o quadrado que serve de base à pirâmide de altura 2 que fica situadaabaixo do plano xOy.• A pirâmide [ABCDE] é semelhante à pirâmide de altura 2 que fica situada abaixo doplano xOy e a razão de semelhança é a razão das alturas.• As bases das pirâmides também são semelhantes com a mesma razão desemelhança.• Se x for o lado do quadrado que é a secção produzida na pirâmide pelo plano xOypodemos escrever: 2 x 4 ×= ⇔ x = 2 ⇔ x =46 4 6 3• E finalmente concluir que a área da secção é2⎛4⎞16A = ⎜ ⇔ A =3⎟⎝ ⎠ 9PROFESSORA: Rosa Canelas 82006/2007