Teoretične osnove

2 Teoretične osnove 

Brez obširnejše razlage so nanizani glavni fizikalni zakoni iz mehanike tekočin in 

termodinamike, ki so potrebni za razumevanje učne snovi v zvezi z energetskimi 

stroji in napravami. Na koncu poglavja je dodanih še nekaj osnov o podobnostnih 

kriterijih. 

2.1 Mehanika tekočin 

2.1.1 Gostota 

Plini in kapljevine se med seboj razlikujejo po gostoti, stisljivosti itn., imajo pa sicer 

mnogo skupnih lastnosti. Z eno besedo se imenujejo tekočine ali s tujko fluidi. Velja: 

dV 

V 

ϱ = dm 

dV 

= dp 

E = dϱ 

ϱ 

ϱ = 

ϱ 0 

1 + ∆p 

E 

(2.1.1) 

(2.1.2) 

(2.1.3) 

pri čemer je ∆p / (N/m 2 ) tlačna razlika in E / (N/m 2 ) modul elastičnosti, preglednica 

2.1. 

Za mnoge praktične primere zadostujejo nekatere poenostavitve, npr. za kapljevine 

vzamemo, da so praktično nestisljive, za pline pa, da se vedejo kot idealni plini, gostota 

plinov se spreminja po plinski enačbi. Pri majhnih spremembah tlakov pogosto 

zadošča, da tudi pline obravnavamo kot nestisljive, npr. tok zraka skozi vetrnice in 

ventilatorje. 

9

10 2 TEORETIČNE OSNOVE 

Tabela 2.1: Modul elastičnosti za nekatere snovi 

Snov Modul elastičnosti 

T / 0 ◦ C E / (N/cm 2 ) 

Benzol 1, 2 · 10 5 

Voda 2, 1 · 10 5 

Živo srebro 2, 9 · 10 6 

Jeklo 2, 1 · 10 7 

2.1.2 Hidrostatični tlak 

Kapljevina lahko sprejema samo tlačne sile. Če zanemarimo njeno težo, deluje hidrostatični 

tlak v notranjosti kapljevine enakomerno na vse strani (Pascalov zakon). 

Dejansko je v večini tehničnih primerov potrebno upoštevati težo kapljevine, hidrostatični 

tlak se namreč povečuje sorazmerno z globino: 

p = p 0 + ϱ · g · ∆H (2.1.4) 

pri tem je p 0 tlak okolice in ϱ gostota kapljevine. 

2.1.3 Vzgon 

Na telo, ki je potopljeno v tekočino, deluje sila vzgona. Ta sila vzgona je enaka teži 

izpodrinjene tekočine. Če telo plava, potem je sila vzgona v ravnotežju s silo teže: 

teža plavajočega telesa je enaka teži izpodrinjene tekočine (Arhimedov zakon): 

F V zg = ϱ · g · V (2.1.5) 

pri tem je V prostornina izpodrinjene tekočine. 

2.1.4 Površinska napetost 

Če povečujemo površino neke tekočine, npr. milnega mehurčka, je treba dovajati 

delo: 

∆W σ = σ · ∆A (2.1.6) 

To delo je sorazmerno povečanju površine mehurčka. Sorazmernostni faktor σ / (N/m 

= J/m 2 ) se imenuje površinska napetost in je pri 20 ◦ C za vodo σ = 72, 75 · 10 −3 

N/m, za veliko večino organskih tekočin pa σ = (20–40) · 10 −3 N/m.

2.1 MEHANIKA TEKOČIN 11 

Zgled. Sile v mehurčku 

Zaradi površinske napetosti je v mehurčku večji tlak, kot pa v okolici. Za kroglasti 

mehurček, ki je potopljen v kapljevini, je to mogoče enostavno izračunati: če 

prerežemo mehurček s premerom d, potem mora biti sila zaradi površinske napetosti 

po obsegu kroga (ϱ · π · d) v ravnotežju s tlačno silo, ki deluje na površino kroga 

(∆p σ · π · d 2 /4) : 

σ · π · d = ∆p σ · π · d2 

4 

V urejeni obliki: 

∆p σ = 4 · σ 

d 

(2.1.7) 

(2.1.8) 

Povečanje tlaka ∆p σ v mehurčku je premo sorazmerno s površinsko napetostjo σ in 

obratno sorazmerno s premerom mehurčka d. 

2.1.5 Kontinuitetna enačba 

Za stacionarni tok tekočine velja: 

∫ 

∫ 

ṁ 1 = ṁ 2 = ϱ 1 · v m1 · dA 1 = 

A 1 

ϱ 2 · v m2 · dA 2 

A 2 

(2.1.9) 

pri tem je ṁ masni tok, ϱ gostota, v m srednja (krajevno povprečena) hitrost tekočine 

in A prerez toka tekočine. Pri majhnih prerezih in zanemarljivih krajevnih spremembah 

hitrosti velja poenostavljen zapis kontinuitetne enačbe: 

ṁ 1 = ṁ 2 = ϱ 1 · v m1 · A 1 = ϱ 2 · v m2 · A 2 (2.1.10) 

2.1.6 Termična enačba stanja 

Veličine stanja p, T in ϱ neke tekočine so med seboj odvisne, povezuje jih termična 

enačba stanja. Za realne tekočine je lahko zveza ϱ = ϱ(p, T ) zelo komplicirana, v 

večini primerov pa so mogoče poenostavitve. Za idealni plin velja plinska enačba: 

p 

ϱ · R · T = 1 (2.1.11) 

Za realne pline se pogosto uporablja korigirana plinska enačba: 

p 

ϱ · R · T = ξ (2.1.12)


Faktor stisljivosti ξ je določen eksperimentalno, odvisen je od snovi, njene temperature 

in tlaka. Navadno je napisan v obliki polinoma, ki je primeren za računalniško 

obdelavo. Za praktični izračun plinov in par, npr. vodne pare, se uporabljajo tudi tabele 

in grafični diagrami. Lastnosti realnih plinov se razlikujejo od idealnih tem bolj, 

čim višji je tlak in čim nižja je temperatura, drugače napisano: čim večja je gostota 

plina. Za vodo in druge nestisljive snovi smemo predpostaviti: 

ϱ = konst. (2.1.13) 

2.1.7 Energijski izrek 

Energijski izrek je za mehaniko tekočin mogoče izpeljati iz osnovnega Newtonovega 

zakona: 

F = 

d(m · v) 

dt 

(2.1.14) 

Obe strani enačbe množimo s prirastkom dolžine dL, katere smer ustreza smeri sile 

F , in predpostavimo m = konst.: 

F · dL = m · dv · dL (2.1.15) 

dt 

Na levi strani dobimo delo dW = F · dL, na desni strani izraz, ki pomeni prirastek 

kinetične energije: m · (dL/dt) · dv = m · v · dv. Od tod sledi energijski izrek 

mehanike, ki pravi, da je delo enako razliki kinetične energije. 

dW = m · v · dv (2.1.16) 

V integralni obliki: 

∆W = m ( ) 

2 · v2 2 − v1 

2 

(2.1.17) 

Če zanemarimo sile med posameznimi atomi, velja energijski izrek tudi za skupek 

atomov neke snovi, pri tem je kinetična energija vsota kinetičnih energij vseh atomov. 

To kinetično energijo sestavljajo: 

• energija, ki jo imajo atomi zaradi svojega neurejenega gibanja (pri idealnih 

plinih ustreza to njihovi notranji energiji dU) in 

• energija, ki ustreza hitrosti težišča celotne plinske mase.


V splošnem ni mogoče določiti, kolikšen del dovedenega dela povečuje notranjo 

energijo in kolikšen del makroskopsko kinetično energijo. V mnogih primerih se 

vse dovedeno delo porablja samo za povečevanje makroskopske kinetične energije. 

Natančno velja to le za nestisljive idealne snovi brez trenja. Ustrezna oblika energijskega 

izreka za ta posebni primer je Bernoullijeva enačba: 

m · p1 + m · g · H 1 + m · v2 1 

ϱ 1 2 = m · p2 + m · g · H 2 + m · v2 2 

ϱ 2 2 

(2.1.18) 

Enačba pove, da se je energija, ki rezultira iz tlaka tekočine in njene zemeljske privlačnosti, 

brez izgub spremenila v kinetično energijo. 

Zgled. Hitrost iztoka kapljevine iz posode 

S kakšno hitrostjo izteka olje iz narisanega cevovoda, če zanemarimo trenje? Razlika 

višin ∆H = 6 m, slika 2.1. Tlak v posodi je enak tlaku na iztoku p 1 = p 2 , začetna 

hitrost (hitrost nižanja gladine) je zanemarljiva: v 1 = 0. Iz Bernoullijeve enačbe 

dobimo: 

ϱ · g · ∆H = ϱ 2 · v2 2 

Od tod je mogoče izračunati izstopno hitrost olja: 

v 2 = √ 2 · g · ∆H = 10,6 m/s 

Hitrost je enaka, kot če bi olje prosto padalo s te višine. 

Slika 2.1: Iztok kapljevine iz posode


Tabela 2.2: Primerjava energijskega in impulznega izreka 

Skalarni energijski izrek 

Newtonov zakon: F = m · dv 

dt 

dL 

F · dL = m · dv 

dt · dL 

dW = m · dL 

dt · dv = m · v · dv 

∆W = m 2 · (v 

2 2 − ) 

v2 1 

Vektorski impulzni izrek 

dt 

F · dt = m · dv 

dI = m · dv 

∆I = m · (v 2 − v 1 ) 

∆ ˙ I = ṁ · (v 2 − v 1 ) = F 

2.1.8 Impulzni izrek 

Tudi impulzni izrek za mehaniko tekočin je mogoče izpeljati iz osnovnega Newtonovega 

zakona, enačba 2.1.14. Obe strani množimo s prirastkom časa dt in predpostavimo 

m = konst.: 

F · dt = m · dv (2.1.19) 

Na levi strani dobimo impulz sile dI = F · dt, na desni strani izraz, ki pomeni 

prirastek hitrosti m · dv. Od tod sledi impulzni izrek, ki pravi, da je impulz sile enak 

spremembi gibalne količine: 

dI = m · dv (2.1.20) 

V tehniki imamo navadno opravka z masnim tokom ṁ in ne z maso m; za stacionarni 

tok velja v integralni obliki: 

∆ ˙ I = ṁ · (v 2 − v 1 ) = F (2.1.21) 

Tok tekočine spreminja pod vplivom zunanje sile F hitrost za ∆v. Ker so sile in 

hitrosti vektorji, je smer sile enaka smeri spremembe hitrosti. Čeprav je impulz vektorska 

veličina in imamo zato na razpolago tri enačbe, je te enačbe navadno lažje 

uporabljati kot pa skalarni energijskih izrek, preglednica 2.2. 

Impulzni izrek, uporabljen za tekočino v kanalu med lopatjem, nam da Eulerjevo 

enačbo, ki je podrobneje obrazložena pri turbinskih strojih. 

Stanje tekočine je v splošnem opisano z gostoto ϱ, temperaturo T , tlakom p in vektorjem 

hitrosti ⃗v(v x , v y , v z ) . Če poznamo snovne lastnosti tekočine (dinamična viskoznost 

η, toplotna prevodnost λ, izobarna in izohorna specifična toplota c p in c v


itd.), je v splošnem na razpolago dovolj enačb za določitev šestih neznank: ϱ, T , 

p, ⃗v(v x , v y , v z ). Prav tako imamo tudi za reševanje problemov na razpolago šest 

enačb: kontinuitetno enačbo, termično enačbo stanja, energijski izrek in tri enačbe 

impulznega izreka. Načelno je tako mogoče za dane razmere (znana geometrija, 

sile in robni pogoji) določiti vsako stanje tekočine. Praktične težave, ki nastanejo 

pri računanju, pa so matematične narave: Navier-Stokesove enačbe (kontinuietna, 

gibalna in energijska enačba v splošni obliki) so namreč nelinearne parcialne diferencialne 

enačbe, ki so analitično nerešljive. 

2.1.9 Trenje v toku 

Doslej še ni bilo omenjeno, da moramo pri tekočinah upoštevati tudi notranje trenje, 

to je, da imamo v tekočini strižne napetosti τ, ki so odvisne od hitrosti te tekočine. 

Če položimo na mokra tla ploščo s ploščino A, lahko ugotovimo, da potrebujemo 

za premikanje plošče neko silo F , slika 2.2. Ta sila je odvisna od ploščine A, od 

hitrosti pomika v, od razdalje med ploščo in tlemi B in od sorazmernostnega faktorja 

η. Sorazmernostni faktor je specifičen za vsako tekočino in ga imenujemo dinamična 

viskoznost: 

F = η · A · v 

B 

(2.1.22) 

splošneje: 

F 

A = τ = η · dv 

dy 

(2.1.23) 

Da izločimo vpliv mase tekočine, delimo dinamično viskoznost z gostoto. To veličino 

imenujemo kinematična viskoznost: ν = η/ϱ. 

Slika 2.2: Strižne sile v tekočini


laminarni tok 

turbulentni tok 

Slika 2.3: Hitrostni profil v cevi okroglega prereza 

V osnovi imamo opravka z dvema vrstama toka. Laminarni tok imenujemo tok, kjer 

potekajo tokovnice po vsem tokovnem prerezu vzporedno. Menjava energije med 

tokovnicami je majhna in je izključno posledica trenja tekočine. V tehniki imamo 

večinoma opravka s turbulentnim tokom: delci tekočine zadevajo drug ob drugega, 

zaradi tega nastane nepravilno gibanje v vzdolžni in prečni smeri toka. Menjava 

energije v tekočini je večja kot pri laminarnem toku in je posledica trenja in medsebojnih 

elastičnih trkov delcev tekočine. Zaradi večje izmenjave energije znotraj toka 

je hitrost toka po celotnem prerezu zelo enakomerna, z izjemo tanke mejne plasti ob 

steni δ, slika 2.3. S kakšnim tokom imamo opravka, nam pove Reynoldsovo število 

Re, ki je eden od brezdimenzijskih kriterijev podobnosti; tok v okroglem cevovodu 

je npr. turbulenten, če je Re > 2300. Več o tem je napisano v poglavju o zakonih 

podobnosti. 

2.1.10 Tlačne izgube v cevovodih in armaturah 

Pri toku tekočin skozi cevi, odcepe, armature itd. pride zaradi notranjega trenja v 

tekočini do izgube tlaka. Za ravno cev velja enačba: 

∆p = λ · L 

d · ϱ · v2 

2 

(2.1.24) 

Izguba specifične tlačne energije ∆p/ϱ je premo sorazmerna z dolžino cevovoda L, 

s kinetično energijo v 2 /2 in obratno sorazmerna s premerom cevovoda d. Sorazmernostni 

faktor λ se imenuje koeficient tekočinskega trenja in ga je mogoče za la-


minarni tok izpeljati matematično iz Navier-Stokesove diferencialne enačbe, Hagen- 

Poiseuillov zakon: 

λ = 64 

(2.1.25) 

Re 

kjer je Re Reynoldsovo število. 

Za turbuletni tok pa je koeficient tekočinskega trenja λ mogoče določiti samo eksperimentalno, 

saj se ga zaradi naključne narave turbulence ne da analitično določiti. 

Za praktično uporabo je primerna Colebrookova poenostavitev Prandtlove enačbe, ki 

velja za celotno turbulentno področje in za hidravlično gladke cevi. Koeficient trenja 

je odvisen samo od Reynoldsovega števila: 

λ = ( 

0,309 ) 2 

(2.1.26) 

lg Re 

7 

V splošnem je koeficient tekočinskega trenja odvisen tudi od hrapavosti stene. Dobre 

rezultate daje zopet Colebrookova enačba z upoštevanjem absolutne hrapavosti 

stene k: 

1 

λ = [ ( )] 

2 · lg 2,51 

2 

(2.1.27) 

Re·√λ + 0,27 · k 

d 

Vrednosti za koeficient tekočinskega trenja λ so navadno prikazane grafično v Moodyjevem 

diagramu, slika 2.4. Diagram prikazuje koeficient trenja za različna Reynoldsova 

števila za gladke in za hrapave cevi. Namesto absolutne hrapavosti k je v 

diagramu vrisana brezdimenzijska relativna hrapavost k/d. Pri tem je merilo hidravlično 

gladke cevi določeno z debelino mejne plasti δ in absolutno hrapavostjo stene 

k. Absolutna hrapavost je za neko cev konstanta, medtem ko se debelina mejne plasti 

zmanjšuje z naraščanjem Reynoldsovega števila: neka cev se pri majhnih pretokih 

vede kot hidravlično gladka, pri velikih pa kot hrapava. Vrednosti srednjih absolutnih 

hrapavosti k za najpogosteje uporabljene cevi so zbrane na sliki 2.5. 

Izgubo tlaka v kolenih, lokih, odcepih, iztokih, priključkih, ventilih, zasunih itd. 

lahko določimo samo z meritvami. Podobno kot pri enačbi za ravne cevi velja: 

∆p = ζ · ϱ · v2 

(2.1.28) 

2 

Pri tem je koeficient izgub ζ navadno tabeliran v priročnikih za posamezne vrste 

armatur. Za gladke okrogle cevi dobimo medsebojno zvezo: 

ζ = λ · L 

d 

(2.1.29)


Slika 2.4: Moodyjev diagram; koeficient tekočinskega trenja λ za ravne okrogle cevi 

v odvisnosti od Reynoldsovega števila Re in relativne hrapavosti k/d


Slika 2.5: Srednje absolutne hrapavosti k najpogosteje uporabljanih cevi 

Zgled. Tlačne izgube v cevovodu 

Kakšne so tlačne izgube v hidravlično gladkem cevovodu iz jeklene valjane cevi zunanjega 

premera 323,9 mm in debeline stene 10,0 mm ter dolžine 260 m, če teče 

skozi cev 780 m 3 /h vode pri 20 ◦ C, dinamična viskoznost vode η = 10 3 kg/(m · s)? 

Predhodno je treba izračunati pomožne veličine: 

Tok vode ˙V = 0,217 m 3 /s 

Notranji premer cevovoda d = 0,3039 m 

Prerez cevovoda A = 0,0725 m 2 

Hitrost vode v cevovodu v = 2,99 m/s 

Reynoldsovo število Re = 907 ′ 760 

Koeficient trenja λ = 0,0118 

Izguba tlaka v cevovodu: 

∆p = λ · L 

d · ϱ · v2 

2 

= 45 ′ 115 Pa = 0,45 bar


2.2 Termodinamika in prenos toplote 

2.2.1 Zakon o ohranitvi energije 

Termodinamika razširja mehaniko tekočin z uvedbo novih oblik energije. V nekem 

določenem in izoliranem sistemu je vsota vseh energij konstantna; napisati smemo, 

da ostane v sistemu konstantna tudi vsota vseh eksergij in anergij. Če se torej v 

sistemu poveča energija ene vrste, se mora zaradi tega v tem istem sistemu zmanjšati 

energija neke druge vrste. Pod imenom sistem je treba razumeti prostor ali pa količino 

snovi, za katero si lahko predstavljamo, da je omejena s stenami. Vse, kar je zunaj teh 

dejanskih ali pa namišljenih sten, je okolica. Tako lahko v splošnem ločimo različne 

termodinamične sisteme: 

• Odprti sistemi: preko meje sistema poteka izmenjava snovi in energije (primer: 

motor z notranjim zgorevanjem). 

• Energijsko odprti (diatermični) sistemi: preko meje sistema je možna samo 

izmenjava energije, ne pa snovi (primer: segrevanje snovi v zaprti posodi). 

• Zaprti sistemi: preko meje sistema ne prehaja niti snov niti energija (primer: 

adiabatna kompresija v zaprti izolirani posodi). 

Delo in toplota sta prehodni energiji, ki delujeta samo na meji med sistemom in 

okolico in se uporabljata za prenos energije; pravimo, da sistem oddaja ali sprejema 

delo in toploto. Razlika med delom in toploto se opazi samo v okolici, ne pa tudi v 

sistemu samem, slika 2.6. Kadar npr. sistem opravlja delo, se to izraža v sočasnem in 

urejenem gibanju vseh delcev v okolici (npr. translatorno gibanje bata). Pri prenosu 

toplote preko meje sistema pa se to izraža kot neurejeno, termično gibanje delcev v 

okolici (npr. termično gibanje molekul tekočine v okolici). 

V tehniki imamo največkrat opravka z odprtimi sistemi, kjer v sistem periodično ali 

zvezno vstopa in izstopa delovna snov. Če upoštevamo vse vrste energij (tlačno, 

kinetično in potencialno) ter masno bilanco, potem lahko za splošni, odprti, neadiabatni, 

stacionarno delujoč sistem zapišemo: 

U 1 + p 1 · V 1 + m · v2 1 

2 + m · g · H 1 + Q 12 = 

= U 2 + p 2 · V 2 + m · v2 2 

2 + m · g · H 2 + W t12 (2.2.1) 

To je oblika energijske enačbe, ki se uporablja pri energetskih strojih, pri čemer se 

indeks 1 nanaša na začetek procesa in indeks 2 na konec procesa, ki poteka na meji 

sistema. Vsota vseh energij in v sistem dovedene toplote Q 12 je enaka vsoti vseh

2.2 TERMODINAMIKA IN PRENOS TOPLOTE 21 

delo 

toplota 

Slika 2.6: Razlika med delom in toploto; A - urejeno gibanje molekul, B - neurejeno 

gibanje molekul 

energij in tehničnemu delu W t12 , ki smo ga dobili na izstopu iz sistema, pri čemer 

velja: m = ϱ · V . Energije ni mogoče niti proizvesti niti uničiti, ampak samo spremeniti 

iz ene oblike v drugo. 

Bernoullijeva enačba je posebna oblika energijske enačbe in velja za tok nestisljive 

tekočine brez upoštevanja trenja, brez dovoda toplote in odvoda tehničnega dela: 

p 1 · V 1 + m · v2 1 

2 + m · g · H 1 = p 2 · V 2 + m · v2 2 

2 + m · g · H 2 (2.2.2) 

Če je sistem namenjen le opravljanju dela, ne pa tudi drugim energijskim pretvorbam, 

se splošni zapis prvega glavnega zakona termodinamike, enačba (2.2.1), poenostavi: 

Q 12 − W t12 = (U 2 + p 2 · V 2 ) − (U 2 + p 2 · V 2 ) (2.2.3) 

kjer sta notranja in tlačna energija (sumanda v vsakem od oklepajev) veličini stanja, 

zato jih lahko nadomestimo z novo veličino stanja - entalpijo: 

Q 12 − W t12 = m · (h 2 − h 1 ) (2.2.4) 

Energijo nekega stacionarno delujočega sistema poveča dovedena toplota Q 12 , zmanjša 

pa jo iz sistema pridobljeno tehnično delo W t12 . Pri odprtih, stacionarno delujočih 

sistemih, je treba delovno snov ves čas dovajati, iztrošeno snov pa odvajati. Pri tem 

potrebujemo stalno polnilno (−p 1 ·V 1 ) in praznilno delo (+p 2 ·V 2 ). Razlika teh dveh 

del je volumensko, imenovano tudi absolutno delo: 

W u12 = W t12 − p 1 · V 1 + p 2 · V 2 (2.2.5)


Slika 2.7: Energetski stroji; A in B - odprti sistem: preko meje sistema prehajata 

zvezno ali periodično snov in energija, C - zaprti sistem: preko meje sistema prehaja 

samo energija 

Polnjenje in praznjenje delovne snovi se opravlja neprekinjeno pri turbinskih ali 

pretočnih strojih in periodično pri volumenskih ali izrivnih strojih, ki imajo sesalne 

in tlačne ventile, slika 2.7. 

V zaprtem sistemu tehničnega dela W t12 nimamo, prvi glavni zakon termodinamike 

pa dobi obliko: 

Q 12 − W u12 = U 2 − U 1 (2.2.6) 

Notranjo energijo zaprtega sistema poveča dovedena toplota Q 12 , zmanjša pa jo 

iz sistema pridobljeno volumensko delo, imenovano tudi delo enkratne ekspanzije 

W u12 . Z enkratno ekspanzijo je ostala delovna snov v energetskem stroju zaprta, njena 

uporabnost je izčrpana, s tem pa je izčrpana tudi uporabnost tega stroja, slika 2.7. 

2.2.2 Krožni procesi 

V tehniki je pomembno pridobivati delo iz toplote stalno in nepretrgoma. Enkratna 

pridobitev dela ni zanimiva. Stalno in zvezno pridobivanje dela pa je mogoče le, če 

se delovna snov po končani ekspanziji vrne v začetno stanje. Da bi se to zgodilo, je 

treba vložiti nekaj dela in odvesti preostanek toplote v okolico. Cilj je, da je pri konstantnem 

dovodu toplote pridobljeno delo čim večje, vloženo pa čim manjše. Take 

procese imenujemo krožne procese, stroje, v katerih ti procesi potekajo, pa energetske 

stroje. 

Pri toplotnih krožnih procesih si preobrazbe v značilnih diagramih p – v ali T – s 

sledijo v smeri urinega kazalca, zato jih imenujemo desni krožni procesi. Toplota 

teče s telesa z višjo temperaturo preko delovne snovi na telo z nižjo temperaturo, pri


Slika 2.8: Shematski prikaz delovanja krožnega procesa 

tem pa se del toplote preobrazi v delo. Take krožne procese uporabljamo v toplotni 

tehniki za pridobivanje mehanskega dela oz. električne energije, slika 2.8A. Levi 

krožni procesi so nasprotni desnim, preobrazbe si sledijo v nasprotni smeri urinega 

kazalca. Vlagamo delo, toploto pa črpamo s telesa z nižjo temperaturo na telo z 

višjo. Take krožne procese uporabljamo v hladilni tehniki in v toplotnih črpalkah, 

slika 2.8B. 

Za proučevanje dejanskih krožnih procesov, ki jih srečamo v tehniški praksi, si pomagamo 

z ustreznimi teoretičnimi, primerjalnimi krožnimi procesi. Najpomembnejši 

taki procesi, ki so termodinamično gledano dobri in ki so se zaradi enostavnosti uveljavili 

v praksi, so zbrani v preglednicah 2.3 in 2.4. Pri tem so vzete za opis procesa 

vedno osnovne termodinamične preobrazbe, kot so izentropa, izoterma, izobara in 

izohora. 

Pri periodično delujočih volumenskih batnih strojih se posamezne preobrazbe v času 

ene periode izvajajo v enem samem stroju, npr. v valju motorja, zato je dogajanja 

najlažje prikazati v diagramu p – v, pri tem vse specifične energije nastopajo kot 

ploščine. 

Pri zvezno delujočih turbinskih strojih pa se posamezne preobrazbe izvajajo v več 

ločenih strojih in napravah, ki so med seboj povezane v postroj ali postrojenje. Ne 

glede na to dejstvo bo zaradi lažje primerjave privzeto, da se vse preobrazbe nanašajo 

na en sam stroj, dogajanja pa so prikazana v diagramu T – s, kjer spet vse specifične 

energije nastopajo kot površine, ali v Mollierovem diagramu h – s, kjer so specifične 

energije prikazane kot daljice.


Tabela 2.3: Termodinamične značilnosti najvažnejših teoretičnih krožnihprocesov 

Carnot Joule Stirling 

1-2 izoterma 3-4 1-2 izentropa 3-4 1-2 izoterma 3-4 

2-3 izentropa 4-1 2-3 izobara 4-1 2-3 izohora 4-1 

Q do Q do Q do 

Q 34 = m · R · T 3 · ln p 3 

p 4 

Q 23 = m · c p · (T 3 − T 2 ) Q 34 = m · R · T 3 · ln p 3 

p 4 

= m · R · T 3 · ln v 4 

v 3 

= m · (h 3 − h 2 ) = m · R · T 3 · ln v 1 

v 2 

Q od Q od Q od 

Q 12 = m · R · T 1 · ln p 2 

p 1 

Q 41 = m · c p · (T 4 − T 1 ) Q 12 = m · R · T 1 · ln p 2 

p 1 

= m · R · T 1 · ln v 1 

v 2 

= m · (h 4 − h 1 ) = m · R · T 1 · ln v 1 

v 2 

W = Q do − Q od W = Q do − Q od W = Q do − Q od 

W = m · R · (T 3 − T 1 ) · ln p 2 

p 1 

W = m · c p · (T 1 − T 2 + T 3 − T 4 ) W = m · R · (T 3 − T 1 ) · ln p 2 

p 1 

= m · R · (T 3 − T 1 ) · ln v 1 

v 2 

= m · (h 1 − h 2 + h 3 − h 4 ) = m · R · (T 3 − T 1 ) · ln v 1 

v 2 

η t = 1 − T 1 

T 3 

η t = 1 − T 1 

T 2 

= 1 − T 4 

T 3 

η t = 1 − T 1 

T 3


Tabela 2.4: Termodinamične značilnosti najvažnejših teoretičnih krožnihprocesov 

Otto Diesel Clausius-Rankine 

1-2 izentropa 3-4 1-2 izentropa 3-4 1-2 izentropa 3-4 

2-3 izohora 4-1 2-3 izobara, 4-1 izohora 2-3 izobara 4-1 

Q do Q do Q do 

Q 23 = m · c v · (T 3 − T 2 ) Q 23 = m · c p · (T 3 − T 2 ) Q 23 = m · (h 3 − h 2 ) 

= m · (u 3 − u 2 ) = m · (h 3 − h 2 ) 

Q od Q od Q od 

Q 41 = m · c v · (T 4 − T 1 ) Q 41 = m · c v · (T 4 − T 1 ) Q 41 = m · (h 4 − h 1 ) 

= m · (u 4 − u 1 ) = m · (u 4 − u 1 ) 

W = Q do − Q od W = Q do − Q od W = Q do − Q od 

W = m · c v · (T 1 − T 2 + T 3 − T 4 ) W = m · 

= m · 

R 

κ−1 · W = m · (h 1 − h 2 + h 3 − h 4 ) 

R 

κ−1 · (T 1 − T 2 + T 3 − T 4 ) ·[κ · (T 3 − T 2 ) + (T 4 − T 1 )] ≈ m · (h 3 − h 4 ) 

η t = 1 − T 4−T 1 

T 3 −T 2 η t = 1 − T 4−T 1 

κ·(T 3 −T 2 ) η t = 1 − h 4−h 1 

h 3 −h 2 

≈ 1 − h 4 

h 3


2.2.3 Delo, moč in izkoristek 

V tehniki je predvsem važno tehnično delo W t , to je delo, ki ga dobimo na gredi 

idealno delujočega ekspanzijskega stroja, pri tem se v delovni snovi zmanjša tlak od 

neke začetne do neke končne vrednosti. 

∫ p2 

W t = m · v · dp (2.2.7) 

p 1 

Podobno velja za kompresijski stroj. Tehnično delo W t je delo, ki ga je treba dovajati 

gredi idealno delujočega kompresijskega stroja, pri tem se v delovni snovi poviša tlak 

od neke začetne do neke končne vrednosti. 

To delo ekspanzije oziroma kompresije, če poteka proces v nasprotni smeri, je v 

diagramu diagramu p – V enako ploskvi p 1 -1-2-p 2 , v diagramu h – s pa daljici 1 - 

2, slika 2.9. Pri tem poteka teoretično ekspanzija ali kompresija delovne snovi po 

izentropi. 

Dejansko tehnično delo je pri ekspanzijskih strojih manjše, in pri kompresijskih strojih 

večje, saj stroji niso idealno delujoči, ampak se pri vseh strojih del energije zaradi 

več ali manj nepopolnih konstrukcij neželeno spremeni v toploto in odteka v okolico. 

Slika 2.9: Tehnični delo idealno delujočega ekspanzijskega oz. kompresijskega stroja


Delo enkratne ekspanzije oziroma kompresije W u je v diagramu p – V enako ploskvi 

pod krivuljo V 1 -1-2-V 2 in je povezano s spremembo prostornine: 

W u = 

∫ V2 

V 1 

p · dV (2.2.8) 

To ekspanzijsko ali kompresijsko delo je tisto, ki ga opravi ali dobi delovna snov, ki 

je v neki zaprti posodi pri eni sami preobrazbi (ekspanziji ali kompresiji). 

Poleg omenjenega tehničnega dela je pri toplotnih krožnih procesih važno delo krožnega 

procesa W ; to je pridobljeno tehnično delo, zmanjšano za vloženo tehnično 

delo, ki je potrebno, da se vrne delovna snov v začetno stanje. Pri Jouleovem krožnem 

procesu je npr. delo krožnega procesa enako delu plinske turbine W tE , zmanjšano za 

delo kompresorja W tK , ki stiska delovno snov na prvotni tlak: 

W = W tE − W tK (2.2.9) 

Moč P je delo W opravljeno v časovni enoti; velja: 

P = dW dt 

= Ẇ (2.2.10) 

Pri vsaki pretvorbi ene vrste energije v drugo imamo opravka z izgubami: del dovedene 

energije se ne spremeni v želeno obliko, npr. v toploto namesto v delo. Izgube 

imajo dva različna izvora in so posledica: 

• narave pretvorbe energij v krožnem procesu in 

• nepopolnih konstrukcij strojev in naprav. 

Merilo za učinkovitost preobrazbe energije je izkoristek. Ta je vedno definiran kot 

razmerje med izkoriščeno in vloženo energijo (delom, toploto) ali med izkoriščenim 

in vloženim energijskim tokom (močjo, toplotnim tokom). Pogosto so izkoristki definirani 

glede na dane merilne možnosti, in sicer tako, da nazorno pokažejo slabosti 

posameznih sklopov stroja ali naprave. V nadaljevanju je navedenih nekaj definicij 

za glavne vrste izkoristkov, ki so pomembni za energetske stroje. Dejansko delo 

ali dejanska moč, ki jo dobimo iz energetskega pogonskega stroja, je torej manjša; 

dejanska moč, ki jo moramo vložiti v energetski delovni stroj, pa večja. 

Pri toplotnih pogonskih strojih imamo opraviti tako s krožnim procesom delovne 

snovi kot tudi s strojem, zato obravnavamo izgube ločeno glede na izvor.


Termični izkoristek toplotnega (pogonskega) stroja 

Termični izkoristek se nanaša zgolj na nepovračljivosti pretvorb energije v krožnem 

procesu. Definiran je kot razmerje med delom ali močjo povračljivo delujočega 

krožnega procesa – torej idealnega stroja – in toploto ali toplotnim tokom, ki preide 

na delovno snov v krožnem procesu. Najboljši termični izkoristek ima povračljiv 

Carnotov krožni proces. Ta je tem večji, čim višja je temperatura dovoda toplote in 

čim nižja je temperatura odvoda toplote. Praktično Carnotovega krožnega procesa ni 

mogoče uresničiti, zato se mu skušamo pri dejanskih krožnih procesih čim bolj približati, 

slika 2.10. Pojem termičnega izkoristka ima smisel samo pri toplotnih krožnih 

procesih; upošteva dejstvo, da je toplota le delno pretvorljiva v delo. 

Q 

η t = 

˙ do − Q ˙ od 

= Ṗ 

(2.2.11) 

Q˙ 

do Q do 

Indicirani in notranji izkoristek 

Pri volumenskih batnih strojih govorimo o indiciranem izkoristku, izračunamo ali 

določimo ga iz indikatorskega diagrama p - v. Pri turbinskih strojih govorimo o notranjem 

izkoristku, izračunamo ali določimo ga iz diagramov T - s ali h - s in je 

primerljiv z indiciranim. Oba, indicirani in notranji izkoristek se nanašata na nepopolne 

izvedbe konstrukcij strojev. 

Slika 2.10: Carnotov in carnotiziran krožni proces; A - izobaren dovod toplote, 

B - izentropna ekspanzija, C - izobaren odvod toplote, Č - izentropna kompresija


Indicirani izkoristek je pri pogonskih strojih razmerje med dejansko močjo na gredi 

stroja in močjo idealno delujočega stroja. Pove, koliko energijskega toka prehaja z 

delovne snovi na bat volumenskega stroja oz. koliko energijskega toka prehaja v 

gonilniku na lopatice turbinskega stroja. Nasprotno je pri delovnih strojih. 

Pogonski stroj: 

η i = P i 

P 

(2.2.12) 

Delovni stroj: 

η i = P P i 

(2.2.13) 

Zmnožek termičnega in notranjega izkoristka: 

η t · η i = 

P i 

˙ Q do 

(2.2.14) 

je razmerje med močjo, ki je na razpolago na gredi toplotnega pogonskega stroja, in 

toplotnim tokom, ki je bil doveden v krožni proces. 

Mehanski izkoristek 

Mehanski izkoristek je pri pogonskih strojih razmerje moči na gredi med strojem in 

generatorjem, pri delovnih strojih pa razmerje moči na gredi med elektromotorjem in 

strojem. Upošteva izgube zaradi trenja v ležajih, drsnikih in vodilih. 


η m = P e 

P i 

(2.2.15) 


η m = P i 

P e 

(2.2.16) 

Dejanski (efektivni) izkoristek 

Dejanski izkoristek je zmnožek posameznih izkoristkov. Pri pogonskih strojih je to 

razmerje med dejansko potrebnim in teoretično izračunanim energijskim tokom. Pri 

delovnih strojih je nasprotno: dejanski izkoristek stroja je razmerje med teoretičnim 

in dejansko vloženim energijskim tokom. 


η e = 

Ṗ · Pi 

Q do P · Pe = P e 

(2.2.17) 

P i Q˙ 

do



η e = P P i 

· Pi 

P e 

= P P e 

(2.2.18) 

Termični izkoristek krožnega procesa je značilnost toplotnih pogonskih strojev, postrojev 

ali postrojenj, medtem ko pri drugih strojih, npr. aerohidravličnih, nima pravega 

smisla, saj pretvorba energije v njih ni vezana na krožni proces (toploto). Termični 

izkoristek η t , ki ima približne vrednosti od 0,5 do 0,6, najmočneje vpliva na 

dejanski izkoristek vsakega toplotnega pogonskega stroja, slika 2.11. 

Če imamo poleg naštetih izgub še druge, npr. izgube zaradi nepopolne toplotne izolacije 

η I , izgube zaradi sevanja η S , izgube zaradi zobniškega ali jermenskega prenosa 

η R itd., velja: 

η e = η t · η i · η m · η I · η S · η R · · · (2.2.19) 


P > P i > P e (2.2.20) 


P e > P i > P (2.2.21) 

Slika 2.11: Shematski prikaz najvažnejših izgub pri pogonskih strojih


2.2.4 Tok tekočin skozi šobe 

Za pravilno delovanje energetskih strojev, posebno turbinskih, je pomembno razumevanje 

toka tekočine skozi kanale. Če v kanalu med dvema turbinskima lopaticama 

hitrost tekočine narašča, statični tlak pa pada, imenujemo tak kanal šoba (konfuzor); 

v nasprotnem primeru govorimo o difuzorju. Tok tekočine skozi šobo ima odločilno 

vlogo pri zasnovi vseh vrst turbinskih strojev (plinskih, parnih in vodnih turbin, turbokompresorjev 

itd.) ter različnih vrst raketnih pogonov. Hitrostne razmere na vstopu 

in na izstopu iz kanala je mogoče določiti z energijsko enačbo. Za izentropni tok 

tekočine (Q 12 = 0), brez opravljanja dela (W t12 = 0) in neupoštevanja potencialne 

energije (H 1 = H 2 ) lahko energijsko enačbo (2.1.1) poenostavimo: 

h 1 + v2 1 

2 = h 2 + v2 2 

2 

(2.2.22) 

Vsota tlačne, notranje in kinetične energije se pri plinskih tokovih pogosto označuje 

s totalno entalpijo, slika 2.12: 

h tot = h + v2 

2 

(2.2.23) 

Slika 2.12: Pretvorba energije pri izentropni ekspanziji


Če pospešujemo plin v šobi iz skoraj mirujočega stanja (v1 2 ≪ v2 2 ) na neko določeno 

izstopno hitrost v 2 , velja energijska enačba v poenostavljeni obliki (primer: turbinska 

stopnja parne turbine): 

√ 

v 2 = 2 · (h 1 − h 2 ) (2.2.24) 

Za idealni plin se enačba (2.2.24) za izstopno hitrost poenostavi (primer: turbinska 

stopnja plinske turbine): 

√ 

v 2 = 2 · c p · (T 1 − T 2 ) (2.2.25) 

Za kapljevine privzamemo, da so nestisljive (ϱ 1 = ϱ 2 = ϱ), notranja energija ostane 

praktično konstantna (U 2 = U 1 ); v tem primeru se energijska enačba nadalje poenostavi, 

slika 2.12 (primer: šoba Peltonove turbine): 

√ 

v 2 = 2 · p1 − p 2 

(2.2.26) 

ϱ 

Če je tlačna energija pred šobo posledica hidrostatičnega tlaka, se hitrost v 2 lahko 

izrazi tudi z višinsko razliko, kot je to prikazano v razdelku 2.1.7. 

V nadaljevanju se bomo omejili na obravnavo izentropnega toka idealnega plina brez 

trenja skozi šobo. Enačbo (2.2.25) preoblikujemo z upoštevanjem: 

• izobarne specifične toplote: 

c p = R · 

κ 

κ − 1 

• termične enačbe stanja idealnega plina: 

(2.2.27) 

T 1 = p 1 

ϱ 1 · R 

(2.2.28) 

• izentropne ekspanzije: 

( ) 1 

ϱ 1 p2 κ 

= 

ϱ 2 p 1 

( ) κ−1 

T 2 p2 κ 

= 

T 1 p 1 

(2.2.29) 

(2.2.30) 

• kontinuitetne enačbe: 

ṁ = ϱ 1 · v 1 · A 1 = ϱ 2 · v 2 · A 2 (2.2.31)


Pri pogoju, da je vstopna hitrost majhna (v1 2 ≪ v2 2 ), izrazimo hitrost in gostoto masnega 

toka na izstopu iz šobe: 

v 2 = 

= 

√ 

2 · c p · T 1 · 

√ 2 · 

κ 

κ − 1 · p1 

ϱ 1 

· 

( 

1 − T ) 

2 

= 

T 1 

[ 

1 − 

( ) 1 

ṁ 

A = ϱ p2 κ 

2 · v 2 = ϱ 1 · · 

p 1 = √ 2 · ϱ 1 · p 1 · √ κ 

κ − 1 · 

( ) κ−1 ] 

p2 κ 

p 1 

[ 

( ) 

√ κ 2 · 

κ − 1 · p1 

κ−1 ] 

p2 κ 

· 1 − 

= 

ϱ 1 p 1 

[ (p2 ) 2 ( ) κ+1 ] 

κ p2 κ 

− = 

p 1 p 1 

(2.2.32) 

= √ 2 · ϱ 1 · p 1 · ψ (2.2.33) 

Slika 2.13: Pretočna funkcija v odvisnosti od tlačnega razmerja


Konvergentna šoba 

V enačbi (2.2.33) vsebuje prvi koren veličine stanja pred šobo (indeks 1), drugi pa 

vrednosti, ki so odvisne samo od plina in od razmerja tlakov za in šobo in pred njo 

(p 2 /p 1 ). Vrednost drugega korena lahko izračunamo za poljubno mesto v šobi, če 

poznamo potek lokalnega tlaka v njej. Imenujemo ga pretočna funkcija: 

ψ(p/p 1 ) = √ κ 

[ ( ) 2 ( ) κ+1 ] 

p κ p κ 

− (2.2.34) 

κ − 1 p 1 p 1 

Za dani plin je v enačbi (2.2.34) eksponent izentrope znan, pretočna funkcija je torej 

odvisna le od razmerja lokalnega tlaka v šobi in tlaka pred njo (p/p 1 ). Pri konvergentni 

šobi je tlačno razmerje na vstopu (p 1 /p 1 ) = 1, nato zaradi pospeševanja toka plina 

pada. Funkcija ima dve ničli: na vstopu pri (p/p 1 ) = 1 in na izstopu (p/p 1 ) = 0, 

slika 2.13. 

Kontinuitetno enačbo za tok idealnega plina v šobi brez trenja lahko zapišemo glede 

na enačbo (2.2.33) v obliki: 

ṁ = A · √2 

· ϱ 1 · p 1 · ψ (2.2.35) 

Da je zadoščeno kontinuitetni enačbi, se mora z zmanjševanjem prereza povečevati 

pretočna funkcija, dokler ne doseže svoje največje vrednosti, pri kateri mora biti 

prerez najmanjši; to pa je lahko pri konvergentni šobi samo na izstopu. Največjo 

vrednost pretočne funkcije dobimo pri pogoju ∂ψ/∂(p 2 /p 1 ) = 0: 

1 

2 · κ · 

p 1 

)kr 

2 · κ 

κ − 1 · 

[ ( ) 2−κ 

2 

κ · 

p2 κ 

− κ + 1 ( ) 1 

p2 κ 

· 

p 1 κ p 1 

] 

= 0 (2.2.36) 

Prvi del zmnožka ne more biti enak nič, pač pa je lahko nič razlika v oglatem oklepaju. 

Po preureditvi dobimo: 

( ( ) κ 

p2 2 κ−1 

= 

(2.2.37) 

κ + 1 

Tabela 2.5: Kritična tlačna razmerja in pripadajoče vrednosti pretočne funkcije za 

različne idealne pline 

Vrsta plina κ (p 2 /p 1 ) kr ψ max 

Enoatomni plini 1,667 0,487 0,514 

Dvoatomni plini 1,400 0,528 0,484 

Triatomni plini 1,300 0,546 0,472 

1,135 0,577 0,449


To je tlačno razmerje, pri katerem doseže pretočna funkcija ψ svojo največjo vrednost, 

imenujemo jo kritično ali Lavalovo razmerje. Največjo vrednost pretočne 

funkcije je mogoče izračunati tako, da vstavimo enačbo (2.2.37) v enačbo (2.2.32). 

Pri kritičnem tlačnem razmerju doseže tudi hitrost v 2 svojo največjo vrednost, imenujemo 

jo kritična ali Lavalova hitrost: 

√ 

[ ( )] 

κ 

v 2 = v kr = 2 · 

κ − 1 · p1 2 

1 − 

ϱ 1 κ + 1 

√ √ 

√ 

2 · κ 

= 

κ + 1 · p1 2 · κ 

= 

ϱ 1 κ + 1 · R · T 1 = 2 · κ − 1 

κ + 1 · c p · T 1 (2.2.38) 

Mogoče je dokazati, da je kritična ali Lavalova hitrost enaka zvočni hitrosti toka. 

Enačba (2.2.38) je v napisani obliki prikladna, saj je kritična hitrost določena z veličinami 

stanja plina pred šobo, ki so navadno znane, slika 2.13 in preglednica 2.5. 

Z upoštevanjem enačb (2.2.30) in (2.2.37) dobimo kritično temperaturo pri kritični 

hitrosti v kr : 

T kr = 2 

κ + 1 · T 1 (2.2.39) 

Če povežemo enačbi (2.2.38) in (2.2.39), dobimo kritično hitrost, izraženo z lokalnimi 

veličinami stanja: 

v kr = √ κ · R · T kr (2.2.40) 

S kakšnimi hitrostmi imamo opravka, nam pove Machovo število, ki je definirano kot 

razmerje med dejansko in kritično hitrostjo plina skozi šobo: 

Ma = v 

v kr 

(2.2.41) 

Tudi Machovo število je – enako, kot že preje omenjeno Reynoldsovo število – eden 

od važnejših brezdimenzijskih kriterijev. Ti bodo opisani v posebnem poglavju. Tlak 

v najmanjšem pretočnem prerezu šobe A min ne pade pod kritičnega, tudi tedaj ne, 

če imamo za šobo vakuum, izstopna hitrost pa ne more biti večja od zvočne hitrosti, 

Ma = 1.


Konvergentno-divergentna šoba 

Gostota masnega toka (ṁ/A) doseže na izstopu iz konvergetne šobe svojo največjo 

vrednost, enačba (2.2.35): 

(ṁ ) 

= √ 2 · ϱ 1 · p 1 · ψ max (2.2.42) 

A 

max 

ali drugače napisano: pri kritičnem tlačnem razmerju je masni tok plina skozi najožji 

ali kritični prerez šobe A min : 

ṁ 

A min 

= √ 2 · ϱ 1 · p 1 · ψ max (2.2.43) 

Glede na enačbo (2.2.43) in lastnost pretočne funkcije ψ, ki doseže največjo vrednost 

pri kritični hitrosti, lahko dobimo večjo hitrost od kritične le, če se začne prerez šobe 

povečevati. Pri nadaljnji ekspanziji prevlada namreč zmanjševanje specifične gostote 

ϱ (večanje specifične prostornine) plina proti povečevanju hitrosti plina. Šobo, ki 

zadostuje temu pogoju, imenujemo konvergento-divergentna ali Lavalova šoba. Sestavljena 

je iz treh delov: 

• konfuzor; podkritično območje, kjer se prerez zmanjšuje, hitrost pa narašča; 

• grlo; najožje mesto, kjer imamo zvočno hitrost in 

• difuzor; nadkritično območje, kjer se prerez povečuje, hitrost pa narašča. 

Izkustvo je pokazalo, da kot v difuzorskem delu šobe ne sme biti večji kot 10–12 ◦ , 

sicer se tok odlepi od sten dufuzorja. 

Krivulje Fanno 

Povezava kontinuitetne (2.1.9) in energijske enačbe (2.2.23) nam da enačbo: 

h tot = h + v2 

2 = h + 1 (ṁ ) 2 

2 · ϱ 2 · 

(2.2.44) 

A 

Ob poznanju totalne entalpije lahko za poljubno gostoto ϱ z enačbo (2.2.44) izračunamo 

specifično entalpijo pri konstantni vrednosti (ṁ/A) in dobimo krivuljo Fanno. 

Drugače napisano, krivulja Fanno podaja vsa možna stanja plina (p, T , ϱ, h, v) pri 

toku skozi določen prerez s konstantno gostoto masnega toka (ṁ/A). 

Na sliki 2.14 so v diagramu h - s narisane krivulje Fanno za konvergentno-divergentno 

šobo za tri različne gostote masnega toka. Vsaka krivulja ima pri ds = 0 

navpično tangento. Glede na drugi stavek termodinamike velja za to točko: 

T · ds = dh − 1 · dp (2.2.45) 

ϱ


Slika 2.14: Krivulje Fanno za tri različne prereze šobe pri konstantni gostoti masnega 

toka 

Z odvajanjem enačbe (2.2.44) po gostoti ϱ dobimo: 

dh − 1 (ṁ ) 2 

ϱ 3 · dϱ = 0 (2.2.46) 

A 

S povezavo enačb (2.1.9), (2.2.45) in (2.2.46) dobimo: 

(ṁ 

A 

) 2 

= 1 ϱ 2 · dp 

dϱ 

(2.2.47) 

in nadalje: 

v kr = 

√ 

dp 

dϱ 

(2.2.48) 

Mogoče je dokazati, da je enačba (2.2.48) identična z enačbo (2.2.40): v točki krivulje 

Fanno z navpično tangento imamo torej kritično ali zvočno hitrost.


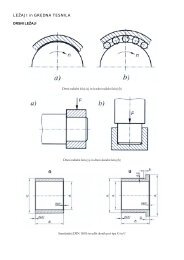
Slika 2.15: Labirintno tesnjenje v diagramu h – s 

Zgled. Labirintno tesnjenje 

Labirintno tesnjenje omogoča tesnjenje rotirajoče gredi glede na mirujoče ohišje turbinskega 

stroja pri poljubno veliki tlačni razliki med notranjostjo stroja in okolico, 

npr.: pri kompresorjih ali pri plinskih in parnih turbinah. 

Dogajanje je mogoče spremljati v diagramu h – s. Skozi labirintne reže enakega 

prereza A teče delovna snov, pri tem ekspandira, zato se močno poveča njena hitrost 

in s tem kinetična energija. V prostoru za režo se kinetična energija delovne snovi 

zaradi vrtinčenja preobrazi v toploto in pri konstantnem tlaku dovaja delovni snovi. 

Postopek se ponovi pri vsakem naslednjem labirintu, pri čemer se tlak od labirinta do 

labirinta zmanjšuje. Proces je adiabaten, zato ostane totalna entalpija nespremenjena. 

Ekspanzija delovne snovi se konča na krivulji Fanno, kot to prikazuje slika 2.15. Pri 

danem začetnem tlaku p 1 , znanem prerezu rež A in številu labirintov je treba s poskušanjem 

več krivulj doseči končni tlak p 2 . Pri premajhnem številu labirintov lahko 

doseže delovna snov zvočno hitrost, kar ni priporočljivo. V nasprotju z navadnim 

tesnjenjem dosežemo pri labirintnih tesnilkah tesnjenje le, če teče skozi vse labirinte 

določena količina delovne snovi.


Tlačni skoki 

Konvergentno-divergentna šoba zahteva za vsako ekspanzijo posebno konstrukcijo. 

Za izbrani protitlak p O je potreben pravilno izračunan izstopni prerez šobe A 2 . In 

nasprotno: vsaki šobi je za izbrani vhodni tlak p 1 potreben točno izračunan izhodni 

tlak p 2 . Slika 2.16 prikazuje v brezdimenzijski obliki potek tlakov vzdolž Lavalove 

šobe za različne protitlake p 2 . 

A 

B 

C 

Č 

D 

E 

p 1 > p O > p A 

Pri prevelikem tlačnem razmerju (p 2 /p 1 ) je tok delovne snovi podoben toku 

v konvergentni šobi, kjer je tlak vedno manjši od kritičnega. V tem tlačnem 

območju tudi v grlu šobe ni dosežena kritična hitrost. 

p O = p B 

Pri zmanjševanju tlačnega razmerja (p 2 /p 1 ) pride v grlu šobe do kritičnega 

tlaka, tok doseže kritično hitrost, ki v difuzorju preide v podkritično. 

p B > p O > p C 

Pri nadaljnjem zmanjševanju tlačnega razmerja (p 2 /p 1 ) doseže tok v grlu šobe 

kritično hitrost, ki nato v difuzorju preide v nadkritično. Ker je protitlak p 2 še 

vedno premajhen, nastane v difuzorju nezvezni tlačni skok iz nadkritičnega v 

podkritično območje. Na izstopu iz šobe je hitrost podkritična. 

Nezvezni tlačni skok je pojav, pri katerem se hitrost delovne snovi v trenutku 

sprevrže iz nadkritične v podkritično. V diagramu h – s se tak tlačni skok izrazi 

kot tlačna sprememba iz nadtlačne v podtlačno krivuljo Fanno. 

p O = pČ 

Tlačno razmerje (p 2 /p 1 ) je toliko zmanjšano, da se tlačni skok premakne na 

izstop difuzorja. Na izstopu iz šobe je tako hitrost kritična. 

pČ > p O > p D 

Tlačno razmerje (p 2 /p 1 ) se zmanjšuje še naprej. V tem območju, ki je nadkritično, 

nastanejo t. i. poševni tlačni skoki. Poševni tlačni skok preide v 

nezveznega, kakor hitro je v območju p B > p O > pČ. Hitrost na izstopu iz 

šobe je kritična. 

p O = p E 

Tlačno razmerje (p 2 /p 1 ) je enako izračunanemu. Tok ekspandira točno po 

izračunani krivulji, zato ni kompresijskih skokov. Hitrost na izstopu iz šobe je 

nadkritična.


F 

p E > p O > p F 

Tlačno razmerje (p 2 /p 1 ) je manjše od izračunanega, dejanski protitlak je nižji 

od računskega (doslej je bil dejanski tlak, razen v primeru E, vedno višji od 

računskega). Tok dokončno ekspandira po izstopi iz šobe. Hitrost na izstopu 

iz šobe je nadkritična. 

Slika 2.16: Tlačne razmere vzdolž Lavalove šobe


2.2.5 Prenos toplote 

Prenos toplote je načelno mogoč na tri načine: s prevodom toplote (kondukcijo), s 

konvekcijo in s sevanjem. 

Prevod toplote 

Prenos toplote je snovnega (npr. molekulskega) izvora in temelji na izmenjavi impulza 

med sosednjimi delci snovi, ki nihajo okrog svojih stalnih ravnotežnih leg. 

Toplota se razširja po notranjosti telesa, s tem da se prenaša z molekul, ki imajo več 

energije (so toplejše) na molekule, ki imajo manj energije (so hladnejše). Pri tem je 

toplotni tok na enoto površine premo sorazmeren s temperaturno razliko in obratno 

sorazmeren z razdaljo med površinama telesa, Fourierjev zakon: 

˙Q 

A = λ · ∆T 

∆y 

(2.2.49) 

Enačba velja za trdna telesa in tekočine. Sorazmernostni faktor je toplotna prevodnost 

λ in je v določenem območju veljavnosti enačbe konstantna vrednost. V splošnem 

pa je toplotna prevodnost funkcija snovi in temperature. 

Podobna zakonitost velja tudi za strižno silo, deljeno s ploščino, torej za strižno napetost 

v toku, primerjaj razdelek 2.1.9, Newtonov zakon: 

F 

A = τ S = η · ∆v 

∆y 

(2.2.50) 

in za spremembo koncentracije snovi, deljeno s ploščino, npr. prenos trdnih delcev 

ṁ 1 v dimnih plinih, Fickov zakon: 

(ṁ ) 

= D · ∆ϱ i 

(2.2.51) 

A ∆y 

S 

Ta analogija velja pri tekočinah samo v primerih, kadar ne prevladuje konvekcija zaradi 

vzgonskih in zunanjih sil, npr. za bližino stene (indeks S), kjer je tok laminaren. 

Za spremembo temperature snovi je bistvena prevodnost λ, za spremembo hitrosti 

viskoznost η, in za spremembo koncentracije snovi difuzija D. 

Konvekcija in konvektivni prestop toplote 

Medtem ko pri prevodu toplota ”pronica” skozi materijo, se pri konvekciji toplota 

prenaša po prostoru z materijo. Transport materije je v tem primeru makroskopski in 

zaradi tega mogoč samo pri tekočinah.


Glede na silo, ki povzroča gibanje tekočine, razlikujemo naravno in prisilno konvekcijo. 

O naravni konvekciji govorimo, če se vzpostavi tok pod vplivom vzgonskih sil 

zaradi razlik gostot. Vzrok za to je lahko razlika temperatur ali razlika koncentracij. 

Pri prisilni konvekciji povzroča tok zunanja sila, npr. sila, ki jo ustvari razlika tlakov. 

O konvektivnem prestopu toplote ali snovi govorimo, če gre za toplotni ali snovni 

tok med tekočino in steno ali če gre za toplotni ali snovni tok neposredno med dvema 

tekočinama. Pri konvektivnem prestopu se ogrejejo delci tekočine, ki pridejo v stik 

s toplejšo steno, potujejo zaradi vzgonskih ali zunanjih sil od stene proč, prenašajo 

toploto, ki so jo sprejeli, na hladnejšo tekočino in končno na hladnejšo steno. 

Konvektivni prestop toplote in snovi opisujeta enačbi: 

˙Q 

A = v · ϱ · c p · ∆T (2.2.52) 

ṁ i 

A = v · ∆ϱ i (2.2.53) 

ki pa praktično nista uporabni, saj se hitrost tekočine v krajevno močno spreminja in 

jo zato ni mogoče določiti. 

Čeprav se dogajanje v sredini toka tekočine razlikuje od dogajanja ob steni (ali na 

meji med dvema tekočinama), je prestop toplote (snovi) mogoče zadovoljivo zajeti z 

veličino α (β), ki upošteva dogajanje ob steni (na meji) in v sredini toka. 

˙Q 

A 

= α · ∆T (2.2.54) 

ṁ i 

A = β · ∆ϱ i (2.2.55) 

Sevanje 

Sevanje je bistveno drugačen način prenosa toplote: ne potrebuje nobenega materialnega 

prevodnika. Pri prenosu toplote s sevanjem je treba omeniti tri faze: 

• pretvorbo termične notranje energije sevajočega telesa v elektromagnetno valovanje 

z valovnimi dolžinami od 0,8 µm do 300 µm; 

• širjenje elektromagnetnega valovanja po prostoru; 

• absorpcijo elektromagnetnega valovanja obsevanega telesa, ponovna pretvorba 

v termično notranjo energijo.


Podobnega prenosa snovi ni. 

Vsako telo s temperaturo večjo od 0 K seva. Količina oddane (sprejete) toplote je odvisna 

od emisivnosti (absorptivnosti) površine telesa, površine same in temperature. 

Emisivnost telesa je enaka njegovi absorptivnosti. Telesu, ki pri določeni temperaturi 

na svoji površini emitira (absorbira) največ sevalne energije, pravimo črno telo. 

Gostota toplotnega toka je premo sorazmerna četrti potenci temperature, Stefanov 

zakon: 

˙Q 

A = ε · σ · T 4 (2.2.56) 

Sorazmernosti faktor je Stefanova konstanta σ = 5, 67 · 10 −8 W/(m 2· K 4 ) za sevanje 

črnega telesa; ε < 1 je emisijski koeficient, ki pomeni razmerje energije, ki jo oddaja 

površina nekega telesa, in energije, ki jo oddaja črno telo. Sevalna moč črnega telesa 

pri temperaturi okolice 300 K je potemtakem: 

˙Q 

A = 5, 67 · 10−8 · 300 4 = 459 W/m 2 (2.2.57) 

Pri prenosu toplote med dvema različno ogretima površinama je treba upoštevati ne 

samo sevanje tople površine, ampak tudi sevanje hladne. 

Prehod toplote 

Pod izrazom prehod toplote razumemo prenos toplote s tekočine z višjo temperaturo 

skozi steno, za katero pa ni nujno, da je prisotna, na tekočino z nižjo temperaturo, 

v splošnem torej zaporedoma: prestop toplote (α 1 ) - prevod toplote (λ) - prestop 

toplote (α 2 ), slika 2.17. 

˙Q 1 = α 1 · A 1 · (T 1 − T S1 ) (2.2.58) 

˙Q S = λ δ · A S · (T S1 − T S2 ) (2.2.59) 

˙Q 2 = α 2 · A 2 · (T S2 − T S2 ) (2.2.60) 

Vsa toplota ali toplotni tok prehaja s tekočine 1 skozi steno v tekočino 2, zato velja: 

˙Q = ˙Q 1 = ˙Q S = ˙Q 2 (2.2.61) 

Če je stena zakrivljena, je potrebno ploščino površine A S nadomestiti s srednjo ploščino 

površine po enačbi: 

A mS = A 1 − A 2 

ln A 1 

A 2 

(2.2.62)


Slika 2.17: Prehod toplote 

Za tanke, zakrivljene stene velja poenostavitev: 

A mS ≈ A 1 ≈ A S ≈ A 2 ≈ A (2.2.63) 

Če napisane enačbe preuredimo tako, da iz njih izpadejo vrednosti T S1 in T S2 , ki so 

le težko merljive, in predpostavimo tanko ravno steno, dobimo: 

( 1 

(T 1 − T S1 ) + (T S1 − T S2 ) + (T S2 − T 2 ) = + δ α 1 λ + 1 ) ˙Q 

· (2.2.64) 

α 2 A 

[ 

] 

˙Q 

A = 1 

· (T 1 − T 2 ) (2.2.65) 

1/α 1 + δ/λ + 1/α 2 

Izraz v oglatem oklepaju se imenuje toplotna prehodnost k, pri čemer so vrednosti α 

in λ eksperimentalno določene in so za vsako tekočino drugačne; pogosto so napisane 

v brezdimenzijski obliki, primerjaj poglavje 2.3. Lastnost koeficienta toplotne 

prehodnosti je, da ne more biti večji od najmanjše toplotne prestopnosti min(α 1 , α 2 ). 

To pomeni, da je treba za izboljšanje toplotne prehodnosti k, npr. prenosnika toplote, 

izboljšati mesto, kjer je toplotna prestopnost α 1 najslabša. Če poznamo številčno 

vrednost za toplotno prehodnost k, lahko izračunamo toplotni tok po enačbi: 

˙Q = k · A · (T 1 − T 2 ) (2.2.66) 

To je ena od najpogosteje uporabljenih enačb pri prenosu toplote. Toplotni tok 

˙Q je torej premo sorazmeren s toplotno prehodnostjo k, s ploščino stene A med 

tekočinama in z razliko temperatur ∆T med toplo in hladno tekočino.


2.2.6 Goriva in zgorevanje 

Goriva 

Goriva so snovi, ki pri višjih temperaturah kemično reagirajo s kisikom (oksidirajo), 

pri tem spremenijo kemično sestavo in sočasno oddajo toploto. Vsebujejo sestavine 

(z malimi črkami so označeni masni deleži posameznih sestavin goriva): 

w c kg ogljika / kg goriva 

w h kg vodika / kg goriva 

kg žvepla / kg goriva 

w s 

w o 

kg kisika / kg goriva 

w v kg vode / kg goriva 

w p kg pepela / kg goriva 

w c + w h + w s + w o + w v + w p = 1 (2.2.67) 

Ogljik C, vodik H 2 in žveplo S so gorljive snovi, voda in pepel so nepotreben in 

odvečen balast. Slabše vrste goriv, npr. trboveljski rjavi premog in velenjski lignit, 

vsebujejo do 50 % negorljivih snovi in vlage. 

Pri stanju okolice je kemična sestava goriv trajno stabilna. Reakcija s kisikom poteka 

vedno pri bistveno višjih temperaturah, kot jo ima okolica, zato so goriva pomembni 

nosilci kemično vezane notranje energije. Nasprotno od drugih virov energije lahko 

kemično vezano energijo goriv pretvorimo v toploto tam, kjer jo potrebujemo, in 

takrat, kadar jo potrebujemo. 

Zgorevalna toplota in kurilnost 

Pomembna veličina za oceno goriva je zgorevalna toplota goriva H s . To je pri izobarnem 

zgorevanju vsa sproščena toplota, ki je enaka razliki entalpij udeleženih snovi 

pred zgorevanjem in po njem. Pri tem predpostavimo, da so v procesu zgorevanja 

vse udeležene snovi ohlajene na 0 ◦ C pri tlaku okolice 1,01325 bar (t. i. normalno 

stanje). 

Za praktično uporabo pa je najpomembnejša kurilnost goriva H i , preglednica 2.6. 

To je tisti del zgorevalne toplote, ki jo dobimo, če ne izkoristimo uparjalne toplote 

vodne pare v dimnih plinih, kar približno ustreza primeru, ko vse produkte zgorevanja 

ohladimo do temperature rosišča. Pri tem je izvor vode v dimnih plinih nepomemben; 

voda lahko nastane iz vodika v gorivu ali pa je prišla v proces zgorevanja kot vlaga v 

gorivu ali zraku. Za procese zgorevanja, kjer je v dimnih prisotna voda, velja: 

H s − H i = w V,D · r (2.2.68) 

pri čemer je w V,D količina vode, nastale pri zgorevanju 1 kg goriva in r kondenzacijska 

(uparjalna) toplota vode, r =2,5 MJ/kg pri 0 ◦ C.


Tabela 2.6: Kurilnosti nekaterih važnejših goriv 

Gorivo 

Kurilnost goriva 

H i / (MJ/kg) 

Antracit 31,82 

Koks 29,31 

Črni premog 27,21 

Rajvi premog 17,52 

Lignit 12,31 

Tekoča goriva 41,87 

Mazut 39,80 

Zemeljski plin 34,10 

Kapljeviti naftni plin 46,00 

Drugi plini ≈20,00 

V večini današnjih tehničnih naprav se izkorišča samo kurilnost goriva, kajti kondenzirana 

vodna para (H 2 O) reagira z žveplovim dvokisom (SO 2 ), ki je v manjših 

količinah pogosto v produktih zgorevanja (navadno jih imenujemo dimni plini), in 

tvori žveplasto (H 2 SO 3 ) in nato žvepleno kislino (H 2 SO 4 ). Kislini sta močno korozivni 

in povzročata škodo na konstrukcijskih materialih. 

Če poznamo kemično sestavo goriva, lahko z zgorevalnimi toplotami posameznih 

sestavin ocenimo kurilnost tega goriva. Za trdna in tekoča goriva velja empirična 

enačba: 

( 

H i = 33, 9 · w c + 121, 4 · 

w h − w o 

8 

) 

+ 10, 5 · w s − 2, 5 · w v (2.2.69) 

Podobne enačbe je mogoče najti v strokovni literaturi tudi za plinasta goriva. 

Zgorevanje 

Zgorevanje je oksidacija goriva pri visokih temperaturah. Proces je eksotermen, pri 

njem se torej sprošča toplota. Pri zgorevanju sproščena kemična energija poveča 

notranjo energijo dimnih plinov in s tem njihovo temperaturo. 

Zgorevanje je popolno, če se vse molekule goriva spojijo s kisikom – oksidirajo; 

v dimnih plinih torej ni več sledi goriva ali produktov delne oksidacije, npr. CO. 

Najvišjo temperaturo dimnih plinov dobimo, če:


• med zgorevanjem toplote dimnih plinov ne odvajamo – imamo adiabatno zgorevanje; 

• je zgorevanje popolno; 

• je zgorevanje stehiometrično, brez presežka kisika. 

Dejanska temperatura dimnih plinov v kuriščih je občutno nižja zaradi spontanega 

odvoda toplote skozi stene, nepopolnega zgorevanja in presežka zraka. Sam proces 

zgorevanja je hiter in nepovračljiv, zato je – eksergijsko gledano – neugoden. 

Zgorevalne procese lahko opišemo s stehiometričnimi enačbami, najvažnejše so: 

C + O 2 = CO 2 + 406,1 MJ/kmol 

1,0 kg C + 2,7 kg O 2 = 3,7 kg CO 2 + 33,9 MJ/kg 

CO + 1 2 O 2 = CO 2 + 282,7 MJ/kmol 

1,0 kg CO + 0,56 kg O 2 = 1,56 kg CO 2 + 10,1 MJ/kg 

H 2 + 1 2 O 2 = H 2 O (para) + 241,9 MJ/kmol 

1,0 kg H 2 + 8,0 kg H 2 O = 9,0 kg H 2 O + 121,0 MJ/kg 

S + O 2 = SO 2 + 296,7 MJ/kmol 

1,0 kg S 2 + 1,0 kg O 2 = 2,0 kg SO 2 + 9,3 MJ/kg 

(2.2.70) 

(2.2.71) 

(2.2.72) 

(2.2.73) 

Pri tem so zaokrožene molske mase M glavnih udeležencev zgorevanja: 

M C = 12 kg/kmol 

M CO = 28 kg/kmol 

M H2 = 2 kg/kmol (2.2.74) 

M S 

= 32 kg/kmol 

M O2 = 32 kg/kmol 

Produkti zgorevanja so torej CO 2 , H 2 O in pogosto tudi SO 2 . Pri nepopolnem zgorevanju 

najdemo v zgorelih dimnih plinih še CO, nezgorele aromate in C (saje), pri 

prevelikem presežku zraka pa SO 3 in O 2 . Dušik N 2 iz zraka teče skozi proces zgorevanja 

praktično nespremenjen, pri visokih temperaturah se deloma veže s kisikom v 

dušikove okside NO, NO 2 , N 2 O 5 itd. (skupna oznaka NO x ). Pri temperaturah nad 

800 ◦ C se začne v večji meri pojavljati disociacija plinov, med seboj začneta reagirati 

tudi inertna plina dušik in kisik.


Tabela 2.7: Razmernik zraka 

Naprava 

Gorilniki plinskih turbin 

Motorji z notranjim zgorevanjem 

Vročevodni in parni kotli 

Razmernik zraka λ 

2−3 

1,0−1,1 

1,05−1,6 

V tehničnih napravah jemljemo kisik za zgorevanje iz zraka; na zemeljski površini 

sestavljata zrak prostorninska deleža kisika ϕ O2 ≈ 21 % in dušika ϕ N2 ≈ 79 %. Navedena 

prostorninska deleža veljata za suh zrak. Navadno imamo opravka z vlažnim 

zrakom, zato je potrebno pri natančnejših računih upoštevati tudi ustrezni delež vode 

v zraku. Najmanjša količina zraka v Zmin , ki je potrebna pri zgorevalnem procesu 1 

kg goriva, je potemtakem: 

v Zmin = v O min 

0, 21 

m 3 /kg (2.2.75) 

kjer je v Omin minimalna količina kisika za popolno zgorevanje izražena s prostornino 

pri temperaturi 0 ◦ C in tlaku 1,01325 bar (normalni kubični meter). Dejanska količina 

zraka, ki je dovedena v zgorevalni prostor, mora biti v praksi večja, da je zgorevanje 

zanesljivo popolno: 

λ = 

v Z 

v Zmin 

> 1 (2.2.76) 

Razmernik zraka λ je definiran kot količnik med dejansko in teoretično potrebno 

količino zraka. Odvisen je od namena zgorevanja, vrste goriva in konstrukcije zgorevalnega 

prostora, preglednica 2.7. 

Za pravilno zgorevanje je treba razmernik zraka stalno nadzorovati, to je še posebej 

pomembno pri vseh vrstah kotlov. Pri premajhnem razmerniku zraka pride do nepopolnega 

zgorevanja; v dimnih plinih se pojavijo CO, aromati in saje, v pepelu pa 

ostajajo ostanki nezgorelega goriva. Pri prevelikem razmerniku zraka se popolnost 

zgorevanja sicer izboljša, toda pri tem se mora segrevati tudi večja količina zraka, 

pretežno sestavljenega iz dušika N 2 , ki pri procesu zgorevanja ne sodeluje, njegova 

toplota pa neizkoriščena odteka v okolico. Posledica prevelikega razmernika zraka 

pa je tudi nižja temperatura zgorevanja, ki vpliva na slabši izkoristek zgorevanja.


Tabela 2.8: Največji možni prostorninski delež ogljikovega dvokisa CO 2 v dimnih 

plinih nekaterih goriv 

Gorivo ϕ CO2 max 

/ % 

Zemeljski plin 11,0−13 

Bencin ≈15,5 

Kurilno olje 15,5−17,5 

Rjavi premog 18,5−19,7 

Lignit 

18,5−20,5 

Les ≈20,5 

Ogljik (oglje) 21 

Razmernik zraka kontroliramo s kemično analizo plinov: merimo količino kisika v 

zgorelih dimnih plinih. Še lažje je določiti razmernik zraka iz izmerjene količine 

ogljikovega dvokisa CO 2 v suhih dimnih plinih, kjer velja za večino trdih in tekočih 

goriv: 

λ = ϕ CO 2 max 

ϕ CO2 

(2.2.77) 

ϕ CO2 max 

je največji možni prostorninski delež ϕ CO2 v suhih dimnih plinih, ki nastane 

pri popolnem zgorevanju brez presežka zraka in je značilna veličina za vsako gorivo, 

preglednica 2.8. Kolikor večji je razmernik zraka pri zgorevanju določenega goriva, 

toliko manjši je dejanski prostorninski delež ϕ CO2 v dimnih plinih. 

Dimni – izpušni plini 

Za produkte zgorevanja se pri kotlih uporablja izraz dimni plini, pri motorjih z notranjim 

zgorevanjem in gorilnikih plinskih turbin pa izraz izpušni plini. Kurilnost H i 

je odvisna od kemične sestave goriva. Na dlani je misel, da mora obstajati odvisnost 

med kurilnostjo na eni strani ter zgorevalnim zrakom in zgorelimi plini na drugi. Na 

osnovi meritev je nastalo več empiričnih enačb za trda, kapljevita in plinasta goriva, 

ki to pričakovanje potrjujejo. Preglednica 2.9 prikazuje take zveze, ki jih je praksa 

dobro potrdila. 

Nadalje se je pokazalo, da se v splošnem ni treba ozirati na kemično sestavo goriva 

in da je srednja specifična toplota dimnih plinov c pD / (kJ/(m 3· K)) približno enaka 

za vse dimne pline, ne glede na vrsto goriva. To velja le kot groba ocena. Ker se 

dimni plini vedejo kot idealni plini, mora biti zato za vsa goriva enaka tudi odvisnost


Tabela 2.9: Izkustveni podatki za minimalno količino zraka in minimalno količino 

dimnih plinov (λ = 1), izraženih v normalnih kubičnih metrih na kilogram goriva 

v odvisnosti od kurilnosti H i / (MJ/kg) trdega ali kapljevitega oz. MJ/m 3 plinastega 

goriva 

Vrsta goriva Kurilnost Minimalna količina Minimalna količina 

H i zraka dimnih plinov 

v Z min / (m 3 /kg) 

v D min / (m 3 /kg) 

oz. (m 3 /m 3 ) oz. (m 3 /m 3 ) 

Trdo MJ/kg 0,241 · H i + 0,50 0,213 · H i + 1,65 

Kapljevito MJ/kg 0,203 · H i + 2,00 0,265 · H i 

Plinasto bogato MJ/m 3 0,260 · H i + 0,25 0,272 · H i + 0,25 

Plinasto revno MJ/m 3 0,209 · H i 0,173 · H i + 1,00 

specifične entalpije dimnih plinov h D / (kJ/m 3 ) od temperature T D pri pogoju, da 

imajo ti dimni plini enak presežek zraka: 

h D = H i 

v D 

(2.2.78) 

kjer je v D / (m 3 /kg) volumen dimnih plinov, izražen na kilogram mase goriva. 

Na sliki 2.18 je prikazana entalpija dimnih plinov v odvisnosti od njihove temperature. 

Vsa toplota, ki se sprosti pri zgorevanju 1 kg goriva s kurilnostjo H i , je vsebovana 

v dimnih plinih, pri tem je bila temperatura vseh udeležencev zgorevanja na 

začetku enaka temperaturi okolice T O . Velja: 

H i = m D · c pD · (T D − T O ) (2.2.79) 

kjer je m D / (kg/kg) je masa dimnih plinov, ki se sprosti pri zgorevanju 1 kg goriva, 

c pD / (kJ/(kg K)) srednja specifična toplota dimnih plinov in T D temperatura dimnih 

plinov. 

Pri gorilnikih plinskih turbin so temperaturne razlike manjše, zato je dopustno vstaviti 

v račune srednjo specifično toploto. Pri motorjih z notranjim zgorevanjem pa 

so temperaturne razlike in tlaki tako veliki, da je treba srednjo specifično toploto 

izračunati po odsekih. Dejanska količina zraka v dimnih plinih, izražena v normalnih 

kubičnih metrih, pa se računa po enačbi: 

v Z,D = v Z − v Z min 

v D 

(2.2.80)


Slika 2.18: h D -T diagram za dimne pline 

Vpliv dimnih plinov na okolico 

Pri vsakem zgorevanju nastanejo v dimnih plinih spojine, ki so za okolico škodljive, 

predvsem: ogljikov dvokis CO 2 in dušikovi oksidi NO x , pogosto tudi žveplov dvokis 

SO 2 . To velja za vse industrijske procese, za termoelektrarne, za motorje z notranjim 

zgorevanjem in tudi za vse zgorevalne procese v široki porabi. 

Ogljikov dvokis CO 2 je eden glavnih povzročiteljev tvorjenja učinkov tople grede 

v ozračju. Drugi plini, ki povzročajo enak učinek, so še metan, dušikovi oksidi in 

freoni. Ti plini, za katere se je udomačilo ime ”toplogredni plini”, tvorijo v zgornjih 

plasteh zemeljskega ozračja sloj, ki ima enak učinek kot steklo v rastlinjakih: 

absorbirajo dolgovalovno energijo sončnega sevanja, se pri tem segrejejo in del te 

akumulirane toplote vračajo na Zemljo. Ta toplota povzroča počasno povečevanje 

povprečne temperature Zemljine atmosfere. 

Dušikovi oksidi NO x , od katerih je najnevarnejši NO 2 , posredno povzročajo tvorjenje 

ozona O 3 in sodelujejo pri tvorjenju toplotne grede. Njihov škodljivi vpliv na okolico 

še ni popolnoma pojasnjen. 

Žveplov dvokis SO 2 , reagira z vlago v dimnih plinih in zraku ter tvori žvepleno kislino. 

Iz ozračja se s časom te kapljice izločijo in padajo na zemljo kot kisli dež. Ta 

uničuje predvsem iglaste gozdove, škodi tudi drugemu rastlinju in povečuje kislost 

zemeljske površine.


2.3 Podobnost in dimenzijska analiza 

2.3.1 Kriteriji podobnosti 

Pri veliki večini energetskih strojev in naprav imamo opravka s turbulentnimi tokovi, 

ki analitično niso rešljivi. Na drugi strani pa je bistven čim bolj natančen preračun 

novega stroja ali naprave, kajti čim večji je stroj, ki ne deluje pravilno, tem dražje 

in časovno daljše so kasnejše spremembe in popravki. Te težave premosti v mnogih 

primerih izdelava primernega, praviloma pomanjšanega modela, ki pa se mora 

skladati z dejansko izvedbo v vseh bistvenih kriterijih podobnosti. Ti so izraženi kot 

brezdimenzijska števila, ki jih v splošnem lahko določimo na dva načina: 

• z zapisom enačb v brezdimenzijski obliki, npr. Navier-Stokesovih enačb, in 

• z dimenzijsko analizo. 

Dva fizikalna pojava sta si podobna, če je vrednost njunih karakterističnih brezdimenzijskih 

števil enaka, s tem je zadoščeno kriterijem podobnosti. Praktična uporabnost 

metode je v tem, da lahko rezultate laboratorijskih meritev na modelu prenesemo na 

realne naprave brez zahtevnega eksperimentalnega preverjanja. V nadaljevanju so 

obravnavani samo nekateri najpomembnejši kriteriji podobnosti s področja prenosa 

impulza, toplote in snovi. 

Model (indeks M) in izvedba (indeks I) si morata biti: 

• geometrijsko podobna (podobnost dolžinskih dimenzij) 

• kinematično podobna (podobnost vektorjev hitrosti in pospeškov) 

• dinamično podobna (podobnost vektorjev sil) 

• termično podobna in 

• snovno podobna 

V praksi se izkaže, da ni mogoče zadostiti vsem kriterijem podobnosti med modelom 

in izvedbo, zato se navadno zadovoljimo z ujemanjem tistih kriterijev podobnosti, ki 

imajo največji vpliv na opazovani pojav. 

Geometrijska podobnost 

Geometrijska podobnost med modelom in izvedbo je osnovni kriterij pri uporabi teorije 

podobnosti. Za njeno izpolnitev morajo biti karakteristične dimenzije modela in 

izvedbe v določenem medsebojnem razmerju:

2.3 PODOBNOST IN DIMENZIJSKA ANALIZA 53 

L M 

L I 

= konst. 

2 

L M 

2 

L I 

= konst. (2.3.1) 

3 

L M 

3 

L I 

= konst. 

Primer za geometrijsko podobnost je brezdimenzijsko število π, razmerje med obsegom 

kroga O in njegovim premerom d: 

π = O d 

(2.3.2) 

Kinematična podobnost 

Kinematična podobnost zahteva, da so si vektorji hitrosti in pospeškov modela in 

izvedbe med seboj proporcionalni. S kriteriji kinematične podobnosti se navadno ni 

treba posebej ukvarjati, saj jim je avtomatično zadoščeno z izpolnjevanjem dinamične 

podobnosti. 

Dinamična podobnost 

Za dosego podobnosti med modelom in izvedbo mora biti zadoščeno kriterijem dinamične 

podobnosti, kjer gre za razmerje sil, ki delujejo na tekočino pri modelu in 

Slika 2.19: Dinamična podobnost tokov na modelu in izvedbi


izvedbi, sočasno pa morata biti izpolnjeni tudi geometrijska ter kinematična podobnost, 

kar pomeni, da morajo za oba sistema veljati enake enačbe. 

Na masni delec tekočine delujejo v splošnem masne, tlačne in viskozne sile, ki so v 

ravnotežju z vztrajnostno silo. Model in izvedba sta si dinamično podobna, če so si 

posamezne sile v poljubni točki opazovanega pojava v sorazmerju, slika 2.19. 

Z dimenzijsko analizo lahko zapišemo za posamezne sile: 

vztrajnostna sila 

viskozna sila 

F v = m · a = ϱ · V · ∆v 

∆t 

∼ ϱ · L 3 · 

v 

L/v = ϱ · v2 · L 2 (2.3.3) 

F η = η · A · ∆vx 

∆y 

∼ η · v · L (2.3.4) 

masna sila teže 

F g = m · g ∼ g · ϱ · L 3 (2.3.5) 

masna sila vzgona 

tlačna sila 

F β = β · g · ϱ · V · ∆T ∼ g · ϱ · β · L 3 · ∆T (2.3.6) 

F p = ∆p · A ∼ ∆p · L 2 (2.3.7) 

tlačna sila z upoštevanjem stisljivosti tekočin v povezavi z enačbo (2.1.2) 

F ξ = ∆p · A = ∆ϱ 

ϱ · E · A ∼ E · L2 (2.3.8) 

Kriterije dinamične podobnosti zapišemo kot razmerja med posameznimi silami. 

Razmerje med vztrajnostno in viskozno silo: 

F v 

= ϱ · v2 · L 2 

F η η · v · L 

= ϱ · v · L 

η 

= v · L 

ν 

= Re (2.3.9) 

kjer je kriterij podobnosti Re Reynoldsovo število. Za podobnost tokov dveh različnih 

tekočin, kjer imata prevladujoč vpliv vztrajnostna in viskozna sila, je dinamična podobnost 

izpolnjena z enakostjo Reynoldsovih števil: 

[ ] [ ] 

Fv Fv 

= ⇒ Re M = Re I (2.3.10) 

F η F η 

M 

I


Razmerje med vztrajnostno in masno silo teže je: 

F v 

= ϱ · v2 · L 2 

F g g · ϱ · L 3 = v2 

g · L = F r (2.3.11) 

kjer je kriterij podobnosti F r Froudovo število. Za podobnost tokov dveh različnih 

tekočin, kjer imata prevladujoč vpliv vztrajnostna sila in masna sila teže, je dinamična 

podobnost izpolnjena z enakostjo Froudovih števil: 

[ ] [ ] 

Fv Fv 

= ⇒ F r M = F r I (2.3.12) 

F g F g 

M 

I 

Razmerje med masno silo vzgona in viskozno silo je: 

F β 

= g · ϱ · β · L3 · ∆T 

F η η · v · L 

= g · β · L3 · ∆T ν 

ν 2 · 

v · L = Gr 

Re 

(2.3.13) 

kjer je kriterij podobnosti kvocient med Gr Grashofovim številom in Re Reynoldsovim 

številom. Za podobnost tokov dveh različnih tekočin, kjer imata prevladujoč 

vpliv masna sila vzgona in viskozna sila, je dinamična podobnost izpolnjena z enakostjo 

Grashofovih števil: 

[ 

g · β · L3 · ∆T 

ν 2 ] 

M 

= 

[ ] 

g · β · L3 · ∆T 

ν 2 

Razmerje med tlačno in vztrajnostno je: 

F p 

F v 

= 

∆p · L2 

ϱ · v 2 · L 2 = 

I 

⇒ Gr M = Gr I (2.3.14) 

∆p = Eu (2.3.15) 

ϱ · v2 kjer je kriterij podobnosti Eu Eulerjevo število (v ameriški literaturi pogosto navedeno 

kot ”pressure coefficient”). Za podobnost tokov dveh različnih tekočin, kjer 

imata prevladujoč vpliv masna sila teže in vztrajnostna sila, je dinamična podobnost 

izpolnjena z enakostjo Eulerjevih števil: 

[ Fp 

F v 

]M 

= 

[ Fp 

F v 

]I 

⇒ Eu M = Eu I (2.3.16) 

Razmerje med vztrajnostno in tlačno silo je pri stisljivih tekočinah (v povezavi z 

enačbama 2.1.2 in 2.2.47 za kritično hitrost): 

F v 

= ϱ · v2 · L 2 

F ξ E · L 2 = v2 

E/ϱ = v2 

vkr 

2 

= Ma 2 (2.3.17)


kjer je kriterij podobnosti Ma Machovo število. Za podobnost tokov dveh različnih 

tekočin, kjer imata prevladujoč vpliv vztrajnostna sila in sila zaradi kompresije ali 

ekspanzije tekočine, je dinamična podobnost izpolnjena z enakostjo Machovih števil: 

[ ] [ ] 

Fv Fv 

= ⇒ Ma M = Ma I (2.3.18) 

F ξ F ξ 

M 

I 

Pri vrednostih Ma < 0, 3 lahko vplive stisljivosti tekočine na tokovno polje zanemarimo. 

Medsebojno povezavo najvažnejših brezdimenzijskih števil, ki pridejo v poštev pri 

prenosu impulza v tekočinah, prikazuje slika 2.20. 

Navadno lahko zadostimo samo enemu kriteriju podobnosti med modelom in izvedbo. 

Kadar je pomembno poznati več vplivov, ki so značilni za tok tekočine, je 

treba meritve ponavljati, tako da je vsakokrat zadoščeno tistemu kriteriju, ki bistveno 

določa tok tekočine. Take meritve so navadno obsežne in drage. 

Slika 2.20: Brezdimenzijska števila pri stacionarnem toku tekočine


Zgled. Ventil za vodik 

Ugotoviti je treba, ali ustreza ventil, ki je vgrajen v cevovodu za zrak, tudi toku 

vodika. Tehnični podatki: 

zrak: T = 20 ◦ C vodik: T = 40 ◦ C 

p = 1 bar 

p = 8 bar 

ν = 1,5 · 10 5 m 2 /s ν = 1,45 · 10 5 m 2 /s 

v = 10 m/s 

v = 10 m/s 

Na tok skozi ventil odločilno vplivata vztrajnostna F v in viskozna sila F η , medtem 

ko smemo vpliv masne sile teže F g in silo zaradi razlike tlakov v cevovodu F p zanemariti. 

Oba tokova skozi ventil sta si podobna, če je izpolnjen kriterij Re Z = Re H . 

[ ] [ ] 

v · d v · d 

= 

ν ν 

Z 

H 

Od tod je mogoče takoj izračunati hitrost vodika v cevovodu: v H = 9,7 m/s. Ventil 

ustreza spremenjenim razmeram, saj je hitrost vodika v cevovodu v normalnih mejah. 

Termična podobnost 

Termična podobnost je težje uporabljiva, saj poleg kriterijev dinamične podobnosti 

zahteva še izpolnjevanje dodatnih kriterijev, ki so značilni za prenos toplote. Poleg 

veličin, ki nastopajo pri dinamični podobnosti, imamo pri termični podobnosti tokov 

še dve novi veličini: toplotni tok ˙Q in temperaturno razliko ∆T . Zveza med toplotnim 

tokom in drugimi veličinami, ki so bistvene za prenos toplote, je določena s 

sorazmernostnimi faktorji, ki pomenijo določeno snovno lastnost, npr. toplotna prevodnost 

λ, toplotna prestopnost α, specifična toplota pri konstantnem tlaku c p itd. 

Podobno kot pri dinamični podobnosti uporabimo dimenzijsko analizo za zapis toplotnega 

toka tudi pri termični podobnosti: 

prevod (kondukcija) toplote 

konvekcija 

˙Q λ = λ · A · ∆T 

∆y 

∼ λ · L · ∆T (2.3.19) 

˙Q K = ṁ · c p · ∆T = ϱ · v · A · c p · ∆T ∼ ϱ · c p · v · L 2 · ∆T (2.3.20) 

konvektivni prestop toplote 

sevanje 

˙Q α = α · A · ∆T ∼ α · L 2 · ∆T (2.3.21) 

˙Q σ = ε · σ · A · ∆T 4 ∼ ε · σ · L 2 · ∆T 4 (2.3.22)


Kriterije termične podobnosti lahko zapišemo kot razmerja med posameznimi toplotnimi 

tokovi, ki morajo biti za primer dinamične podobnosti tokov enaka za model in 

izvedbo. 

Razmerje med konvektivnim prestopom in prevodom toplote je: 

˙Q α 

˙Q λ 

= α · L2 · ∆T 

λ · L · ∆T 

= α · L 

λ 

= Nu (2.3.23) 

kjer je kriterij podobnosti Nu Nußeltovo število. Pri obravnavi prenosa toplote z ene 

snovi na drugo, kjer imata prevladujoč vpliv konvektivni prestop in prevod toplote, 

je termična podobnost izpolnjena z enakostjo Nußeltovih števil: 

[ ] ˙Q α 

˙Q λ 

M 

= 

[ ] ˙Q α 

˙Q λ 

I 

⇒ Nu M = Nu I (2.3.24) 

Razmerje med konvekcijo in kondukcijo (prevodom toplote) je: 

˙Q K 

˙Q λ 

= ϱ · c p · v · L 2 · ∆T 

λ · L · ∆T 

= ϱ · c p · v · L 

λ 

= P e (2.3.25) 

kjer je kriterij podobnosti P e Pecletovo število. Podobno kot je Reynoldsovo število 

razmerje med turbulentim in laminarnim prenosom impulza v tekočini, je Pecletovo 

število razmerje med konvekcijo in kondukcijo. Pri prenosu toplote, kjer imata prevladujoč 

vpliv na porazdelitev temperatur konvekcija in kondukcija, je termična podobnost 

izpolnjena z enakostjo Pecletovih števil: 

[ ] ˙Q K 

˙Q λ 

M 

= 

[ ] ˙Q K 

˙Q λ 

I 

⇒ P e M = P e I (2.3.26) 

Pogosto se namesto Pecletovega števila uporablja Prandtlovo število P r, ki je kvocient 

Pecletovega in Reynoldsovega števila: 

P r = ˙Q K 

· Fη = η · c p 

˙Q λ F v λ 

= P e 

Re 

(2.3.27) 

Iz zgornjega izraza je razvidno, da je Prandtlovo število funkcija snovnih lastnosti 

tekočine P r = P r(p, T ). Vrednosti za snovne lastnosti so navadno navedene v termodinamičnih 

tabelah ali diagramih. Prandtlovo število je pomemben pokazatelj pri 

opisu prenosa toplote, ker vsebuje informacijo o razmerju med debelino hidravlične 

in termične mejne plasti. Tako pomeni neposredno povezavo med hitrostnim in temperaturnim 

poljem toka tekočine.


Razmerje med konvektivnim prestopom toplote in konvekcijo je: 

˙Q α 

˙Q K 

= 

α · L 2 · ∆T 

ϱ · v · c p · L 2 · ∆T = 

α 

ϱ · v · c p 

= St (2.3.28) 

kjer je podobnostni kriterij St Stantonovo število. To število je mogoče izraziti tudi s 

kombinacijo že znanih brezdimenzijskih števil: 

St = Nu 

P e = 

Nu 

Re · P r 

Razmerje med sevanjem in prevodom toplote je: 

˙Q σ 

˙Q λ 

= ε · σ · L2 · ∆T 4 

λ · L · ∆T 

= ε · σ · L · ∆T 3 

λ 

(2.3.29) 

= Sf (2.3.30) 

kjer je kriterij podobnosti Sf Stefanovo število. Pri prenosu toplote, kjer imata prevladujoč 

vpliv na porazdelitev temperatur sevanje in prevodnost, je termična podobnost 

izpolnjena z enakostjo Stefanovih števil: 

[ ] ˙Q σ 

˙Q λ 

M 

= 

[ ] ˙Q σ 

˙Q λ 

I 

⇒ Sf M = Sf I (2.3.31) 

Medsebojno povezavo najvažnejših brezdimenzijskih števil, ki pridejo v poštev pri 

prenosu toplote, prikazuje slika 2.21. 

Slika 2.21: Brezdimenzijska števila pri stacionarnem prenosu toplote


Slika 2.22: Podobnost modela in izvedbe pri prisilni konvekciji 

Na sliki 2.22 sta narisani dve tokovni polji in v teh poljih dva valja. Z vidika prisilne 

konvekcije sta si toka podobna, če so izpolnjeni naslednji pogoji: 

• geometrijska podobnost: velikost valjev in velikost območja opazovanja sta si 

proporcionalni; 

• kinematična podobnost: porazdelitvi hitrosti na mejah območja opazovanja sta 

si podobni po velikosti in smeri; 

• dinamična podobnost: enakost Reynoldsovih števil v območju opazovanja, 

Re M = Re I ; 

• termična podobnost: enakost Prandtlovih in Nußeltovih števil v območju opazovanja, 

P r M = P r I in Nu M = Nu I . Enakost Prandtlovih števil kaže na 

proporcionalnost temperaturnega polja, enakost Nußeltovih pa na proporcionalnost 

prestopa toplote. 

Iz omenjenega primera za prisilno konvekcijo je razvidno, da se kriterij termične 

podobnosti lahko izrazi s funkcijsko povezavo Nu = Nu(Re, P r). Pri naravni konvekciji 

na tok tekočine bistveno vpliva masna sila vzgona, zato namesto Reynoldsovega 

števila v kriteriju termične podobnosti nastopa Grashofovo število: Nu = 

Nu(Gr, P r). 

Eksperimentalne raziskave so pokazale, da je mogoče empirične enačbe za števila 

Nu prikazati v potenčni obliki: 

Nu = K · Gr m · P r n naravna konvekcija (2.3.32) 

Nu = K · Re m · P r n prisilna konvekcija (2.3.33)


Konstanta K in eksponenta m in n so določeni z meritvami za vsako izvedbo prenosnika 

toplote posebej. Če na prenos toplote vplivajo še druge okoliščine toka, npr. 

geometrija telesa, stisljivost tekočine itd., je treba enačbe ustrezno razširiti in z meritvami 

določiti nove konstante. Empirične enačbe so zbrane v tehniških priročnikih in 

drugi literaturi, ki obravnava prenos toplote. Pri enačbah je navedeno tudi območje 

veljavnosti takih enačb. Primer praktične enačbe za prestop toplote na steno okrogle 

cevi za stacionarni turbuletni tok: 

Nu = α · d 

λ 

= 0,0235 · (Re 0,8 − 230) · (1,8 · P r 0,3 − 0,8) · 

· 

[ ( ] ( ) d 3 P r 0,14 

1 + · 

L)2 

P r S 

(2.3.34) 

Enačba velja v območju Re > 2300 in 0,7 

upošteva vpliv dolžine cevi L: na začetku cevi imamo namreč nerazvito mejno 

plast, prestop toplote je zato boljši. Mejna plast postaja z naraščajočo dolžino cevi 

debelejša, prestop toplote se slabša. Zadnji člen v enačbi upošteva vpliv spremembe 

snovnih lastnosti zaradi razlike temperatur tekočine na sredini cevi in ob steni. Omenjeni 

vpliv je majhen in je ga treba upoštevati le, kadar so te temperaturne razlike 

velike. 

Zgled. Prestop toplote iz tekočine na steno cevi 

Določiti je treba toplotno prestopnost α za kotlovsko cev, v kateri teče vroča voda, za 

naslednje tehnične podatke: 

T = 150 ◦ C 

p = 150 bar 

d = 0,038 m 

L = 20 m 

v = 3,0 m/s 

Iz tabel za lastnosti vode in vodne pare povzamemo: 

ϱ = 925,1 kg/m 3 

c p = 4,263 kW/(kg K) 

λ = 691,8·10 6 kW/(m K) 

η = 186,1·10 6 kg/(m s)


Iz navedenih podatkov izračunamo manjkajoče vrednosti: 

P r = η · c p 

λ = 186,1 · 10−6 · 4,263 

691,8 · 10 −6 = 1,147 

( P r 

P r S 

) 0,14 

≈ 1 

Re = ϱ · v · d 

η 

= 

Enačba (2.3.34) za prestop toplote: 

925,1 · 3,0 · 0,038 

186,1 · 10 −6 = 566 ′ 692 

Nu = 0,0235 · (566 ′ 692 0,8 − 230) · (1,8 · 1,147 0,3 − 0,8) · 

[ ( ) 2 

] 

0,038 3 

· 1 + 

= 1022 

20 

Povprečna toplotna prestopnost z vode na steno cevi je: 

α = λ d 

· Nu = 

691,8 · 10−6 

0,038 

· 1022 = 18,6 kW/(m 2 · K) 

Snovna podobnost 

Pogosto imamo opraviti z dvo- ali večfaznimi sistemi, torej sistemi, v katerih nastopajo 

snovi (tekočine) različnih gostot ali agregatnih stanj. Primer take naprave je 

hladilni stolp. Na meji med tekočinama – med zrakom in hladilno vodo – poteka poleg 

intenzivnega prenosa toplote tudi izmenjava snovi v obeh smereh: voda prehaja 

na zrak in v manjši meri zrak v hladilno vodo. Pri snovni podobnosti imamo dve 

novi veličini: masni tok i-te komponente ṁ i , ki prestopa iz ene tekočine v drugo, 

in razlika gostot i-te komponente ∆ϱ i (razlika gostot je večkrat definirana tudi kot 

razlika parcialnih tlakov ali kot razlika koncentracije i-te komponente v eni in drugi 

tekočini). Mehanizmi prenosa snovi so popolnoma primerljivi z mehanizmi prenosa 

toplote. Tudi pri prenosu snovi je zveza med masnim tokom i-te komponente in 

drugimi veličinami določena s sorazmernostnimi faktorji, ki predstavljajo določeno 

snovno lastnost, npr. difuzija D, snovna prestopnost β. 

Snovno podobnost je mogoče izraziti podobno kot termično podobnost: 

difuzija 

ṁ i,D = D i · A · ∆ϱ i 

∆y 

∼ ϱ · D · L (2.3.35)


Difuzijski prenos snovi, ki je posledica razlike gostot i-te komponente, ki prehaja 

iz ene tekočine na drugo, je primerljiv s prevodom toplote, ki je posledica razlike 

temperatur. 

snovna konvekcija 

ṁ i,K = v · A · ∆ϱ i ∼ ϱ · v · L 2 (2.3.36) 

Prenos snovi zaradi konvekcije je posledica gibanja, enako kot je to pri prenosu toplote. 

konvektivni prestop snovi 

ṁ i,β = β · A · ∆ϱ i ∼ ϱ · β · L 2 (2.3.37) 

Tudi kriterije snovne podobnosti lahko zapišemo – enako kot pri termični podobnosti 

– kot razmerja med posameznimi snovnimi tokovi, ki morajo biti za primer dinamične 

podobnosti tokov enaka za model in izvedbo. 

ṁ i,β 

= ϱ · β · L2 

ṁ i,D ϱ · D · L = β · L = Sh (2.3.38) 

D 

kjer je kriterij podobnosti Sh Sherwoodovo število - analogno kot Nußeltovo število 

pri konvektivnem prestopu toplote. Pri obravnavi prenosa snovi i-te komponente iz 

ene snovi na drugo, npr. hlapenje vode v zrak, kjer imata prevladujoč vpliv konvektivni 

prehod in difuzija snovi, je snovna podobnost izpolnjena z enakostjo Sherwoodovih 

števil: 

[ ] 

ṁi,β 

ṁ i,D 

M 

= 

[ ] 

ṁi,β 

ṁ i,D 

I 

⇒ Sh M = Sh I (2.3.39) 

Razmerje med konvekcijo in difuzijo, viskozno in vztrajnostno silo je: 

ṁ i,K 

· Fη = ϱ · v · L2 

ṁ i,D F v ϱ · D · L · η · v · L 

ϱ · v 2 · L 2 = ν D 

= Sc (2.3.40) 

kjer je kriterij podobnosti Sc Schmidtovo število - analogno kot Prandtlovo število 

pri termični podobnosti. Tudi Schmidtovo število je snovna lastnost in pomeni pomembno 

povezavo med hitrostnim in koncentracijskim poljem dveh sistemov. 

Razmerje med konvektivnim prestopom snovi in konvekcijo je: 

ṁ i,β 

ṁ i,K 

= ϱ · β · L2 

ϱ · v · L 2 = β v = St II (2.3.41)


kjer je kriterij podobnosti St II Stantonovo II število - analogno kot Stantonovo število 

pri konvektivnem prestopu toplote. Stantonovo II število je mogoče izraziti tudi s 

kombinacijo že znanih brezdimenzijskih števil: 

St II = 

Sh 

Re · Sc 

(2.3.42) 

Preurejena enačba (2.3.34) za prestop snovi na steno okrogle cevi za stacionarni turbuletni 

tok: 

Sh = α · d 

λ 

= 0,0235 · (Re 0,8 − 230) · (1,8 · Sc 0,3 − 0,8) 

· 

[ ( ] ( ) d 3 Sc 0,14 

1 + · 

L)2 

Sc S 

(2.3.43) 

Enačba velja pri enakih robnih pogojih kot enačba (2.3.34): Re > 2300 in 0, 7 < 

Sc < 1000. Izvrednotena in grafično prikazana je na sliki 2.23. 

Slika 2.23: Pregledni diagram za določitev toplotne in snovne prestopnosti za stacionarni 

turbuletni tok v okrogli cevi


2.3.2 Dimenzijska analiza 

V primerjavi s posameznim fizikalnim pojavom, kot je npr. tok tekočine v cevi, 

je delovanje stroja mnogo bolj zapleteno, zato v večini primerov ne poznamo vseh 

enačb, ki bi omogočale določitev brezdimenzijskih števil. V tem primeru s pridom 

uporabimo dimenzijsko analizo, imenovano tudi Buckinghamov ali Π-teorem: vsako 

dimenzijsko pravilno enačbo je namreč mogoče zapisati kot povezavo brezdimenzijskih 

števil. Dimenzijsko pravilna enačba: 

f(x 1 , x 2 , . . . , x n ) = 0 (2.3.44) 

kjer so x 1 , x 2 , . . . , x n poljubne dimenzijske veličine, pomembne za opis nekega fizikalnega 

pojava, je torej mogoče zapisati tudi v brezdimenzijski obliki: 

F (Π 1 , Π 2 , . . . , Π m ) = 0 (2.3.45) 

Število karakterističnih brezdimenzijskih števil je m = n − i, pri tem je n število 

fizikalnih veličin in i število osnovnih mer. Tako se zmanjša razsežnost opazovanega 

fizikalnega pojava na m brezdimenzijskih produktov n fizikalnih veličin. To 

omogoča pri raziskavah strojev in naprav bistveno zmanjšanje eksperimentalnega in 

teoretičnega dela. Razen tega lahko izmerjene ali izračunane karakteristike različnih 

strojev ali naprav, ki so podane v brezdimenzijski obliki, neposredno medsebojno 

primerjamo, ker so neodvisne od uporabljenega merskega sistema. Navadno uporabljamo 

mednarodni SI-sistem. 

Za mehanske probleme je število osnovnih mer i = 3, npr. dolžina L, čas T in masa 

M, pri termičnih pa i = 4, potrebna je še temperatura Θ. Posamezne veličine, ki 

so značilne za določen fizikalni pojav ali delovanje posameznega stroja ali naprave, 

lahko torej zapišemo z osnovnimi merami, najvažnejše so zbrane v preglednici 2.10. 

Oznake za osnovne mere so v tem poglavju prilagojene ustaljeni praksi in ne odgovarjajo 

siceršnjim oznakam v knjigi. 

Za uporabo dimenzijske analize je treba za opazovani fizikalni pojav poznati vse 

bistvene fizikalne veličine, saj sicer ne dobimo ustrezne množice brezdimenzijskih 

števil. V nadaljevanju je uporaba dimenzijske analize prikazana na treh značilnih 

primerih iz energetskega strojništva.


Tabela 2.10: Mere nekaterih napogosteje uporabljenih fizikalnih veličin v mednarodnem 

merskem sistemu SI 

Fizikalna veličina Oznaka Osnovna mera 

Dolžina 

L 

Višina H L 

Premer 

d 

Absolutna hrapavost 

k 

Ploščina A L 2 

Prostornina, volumen V L 3 

Čas t T 

Hitrost v L · T −1 

Pospešek 

a 

Zemeljski pospešek 

g 

L · T −2 

Volumenski tok ˙V L3 · T −1 

Vrtilna frekvenca 

f 

Kotna hitrost ω T −1 

Vrtilna frekvenca 

n 

Kinematična viskoznost ν L 2 · T −1 

Snovna difuzivnost 

D 

Masa m M 

Gostota ϱ M · L −3 

Dinamična viskoznost η M · L −1 · T −1 

Sila F M · L · T −2 

Tlak 

p 

Napetost (mehanska) σ, τ 

M · L −1 · T −2 

Masni tok ṁ M · T −1 

Delo, energija 

W 

Toplota Q M · L 2 · T −2 

Moment sile 

M 

Moč 

P 

Toplotni tok 

˙Q 

M · L 2 · T −3 

Temperatura T Θ 

Plinska konstanta 

R 

Izobarna spec. toplota c p L 2 · T −2 · Θ −1 

Izohorna spec. Toplota c v 

Toplotna prevodnost λ M · L · T −3 · Θ −1


Zgled. Tlačne izgube v okrogli cevi 

V preglednici 2.11 so podane najvažnejše fizikalne veličine, ki vplivajo na tok tekočine. 

Na osnovi teh veličin je mogoče z dimenzijsko analizo določiti najvplivnejša 

karakteristična brezdimenzijska števila, ne da bi pri tem uporabili znane enačbe za 

tok viskozne tekočine v okrogli cevi. 

Tabela 2.11: Fizikalne veličine za tok viskozne tekočine v cevi 

Fizikalna Zmanjšanje tlaka, Dinamična Absolutna Premer Hitrost Gostota 

veličina deljeno z dolžino viskoznost hrapavost 

Eksponent a b c č d e 

Oznaka ∆p/L η k d v ϱ 

Mera M · L −2 · T −2 M · L −1 · T −1 L L L · T −1 L · T −3 

Tok v cevi je podan kot funkcija šestih spremenljivk n = 6: 

f( ∆p , η, k, d, v, ϱ) = 0 (2.3.46) 

L 

Število mer obravnavanega primera je i = 3, fizikalni pojav lahko zato zapišemo kot 

funkcijo treh brezdimenzijskih števil m = n − i = 3: 

F (Π 1 , Π 2 , Π 3 ) = 0 (2.3.47) 

Splošno karakteristično brezdimenzijsko število obravnavanega problema je: 

Π . = (M · L −2 · T −2 ) a · (M · L −1 · T −1 ) b · 

· (L) c · (L)č · (L · T −1 ) d · (M · L −3 ) e = (2.3.48) 

= M a+b+e · L −2a−b+c+č+d−3e · T −2a−b−d 

Ob pogoju, da je Π brezdimenzijsko število, mora biti vsota eksponentov vsake mere 

enaka nič, zato dobimo za vsako brezdimenzijsko število Π sistem treh linearnih 

enačb s šestimi neznankami. Izbira treh eksponentov je poljubna, preostale tri pa 

izračunamo. Število trojic karakterističnih brezdimenzijskih števil je neskončno veliko, 

v praksi pa vzamemo vedno kombinacijo Π 1 , Π 2 , Π 3 , ki imajo fizikalni pomen. 

V preglednici 2.12 so za vsako karakteristično brezdimenzijsko število podane izbrane 

vrednosti eksponentov a, b in c ter izračunane vrednosti preostalih treh eksponentov 

po enačbah: 

a + b + e = 0 

−2 · a − b + c + č + d − 3 · e = 0 

−2 · a − b − d = 0


Če za Π 1 izberemo vrednosti eksponentov: a = 1, b = 0 in c = 0, lahko izračunamo 

preostale tri eksponente: 

⎫ 

1 + 0 + e = 0 ⎪⎬ č = 1 

−2 − 0 + 0 + č + d − 3 · e = 0 

−2 − 0 − d = 0 

⎪⎭ ⇔ d = −2 

(2.3.49) 

e = −1 

Enako izračunamo vrednosti eksponentov za brezdimenzijska števila Π 2 in Π 3 . 

Tabela 2.12: Matriki izbranih in izračunanih eksponentov za tok viskozne tekočine v 

cevi 

Izbrani eksponenti 

a b c 

Π 1 1 0 0 

Π 2 0 1 0 

Π 3 0 0 1 

Izračunani eksponenti 

č d e 

Π 1 1 −2 −1 

Π 2 −1 −1 −1 

Π 3 −1 0 0 

Karakteristična brezdimenzijska števila Π 1 , Π 2 in Π 3 , ki opisujejo viskozni tok v 

cevi, so tako določena: 

Π 1 = 

( ) ∆p a 

· (η) b · (k) c · (d)č · (v) d · (ϱ) e = ∆p 

L 

ϱ · v 2 · d 

L = Eu · d 

L (2.3.50) 

Brezdimenzijsko število Π 1 je za poznano geometrijo cevi sorazmerno Eulerjevem 

številu. 

( ) ∆p a 

Π 2 = · (η) b · (k) c · (d)č · (v) d · (ϱ) e η 

= 

L 

ϱ · v · d = 1 (2.3.51) 

Re 

Brezdimenzijsko število Π 2 je obratno sorazmerno Reynoldsovem številu. 

Π 3 = 

( ) ∆p a 

· (η) b · (k) c · (d)č · (v) d · (ϱ) e = k L 

d 

(2.3.52) 

Brezdimenzijsko število Π 3 je poznano kot relativna hrapavost.


Tok viskozne tekočine v cevi je funkcija treh karakterističnih brezdimenzijskih števil: 

( ∆p 

F (Π 1 , Π 2 , Π 3 ) = F 

ϱ · v 2 · d 

L , 1 

Re , k ) 

= 0 (2.3.53) 

d 

Izguba tlaka je navadno prikazana kot funkcijska odvisnost od preostalih dveh brezdimenzijskih 

števil Π 2 in Π 3 : 

∆p = φ(Π 2 , Π 3 ) · ϱ · v 2 · L 

d = λ 2 · ϱ · v2 · L 

d 

(2.3.54) 

kjer funkcijo φ(Π 2 , Π 3 ) izrazimo s koeficientom tekočinskega trenja λ, ustrezno 

enačbi (2.1.24): 

φ(Π 2 , Π 3 ) = φ(Re, k/d) = 

λ(Re, k/d) 

2 

(2.3.55) 

Zgled. Brezdimenzijske karakteristike hidravličnih turbinskih strojev 

V preglednici 2.13 so podane najvažnejše fizikalne veličine, ki vplivajo na delovanje 

hidravličnih turbinskih strojev, kot so turbinske črpalke in vodne turbine. Enako kot v 

prejšnjem zgledu bodo z dimenzijsko analizo določena najvplivnejša karakteristična 

brezdimenzijska števila. Za izračun privzamemo nestisljivost tekočine in konstantno 

temperaturo toka. 

Tabela 2.13: Fizikalne veličine za hidravlične turbinske stroje 

Fizikalna Moč na Spec. Izkoristek Dinamična Volumenski Gostota Vrtilna Premer 

veličina gredi energija viskoznost tok frekvenca rotorja 

Eksponent a b c č d e f g 

Oznaka P gH η νϱ ˙V ϱ n d 

Mera M · L 2 · T −3 L 2 · T −2 - M · L −1 · T −1 L 3 · T −1 M · L −3 T −1 L 

Karakteristika hidravličnega turbinskega stroja je podana kot funkcija osmih spremenljivk 

n = 8: 

f(P, gH, η, νϱ, ˙V , ϱ, n, d) = 0 (2.3.56) 

Število mer obravnavanega primera je i = 3, primer lahko zato zapišemo kot funkcijo 

petih brezdimenzijskih števil m = n − i = 5: 

F (Π 1 , Π 2 , Π 3 , Π 4 , Π 5 ) = 0 (2.3.57)


Tabela 2.14: Matriki izbranih in izračunanih eksponentov za hidravlične turbinske 

stroje 



a b c č d 

Π 1 1 0 0 0 0 

Π 2 0 1 0 0 0 

Π 3 0 0 1 0 0 

Π 4 0 0 0 1 0 

Π 5 0 0 0 0 1 

e f g 

Π 1 −1 −3 −5 

Π 2 0 −2 −2 

Π 3 0 0 0 

Π 4 −1 −1 −2 

Π 5 0 −1 −3 


Π . = (M · L 2 · T −3 ) a · (L 2 · T −2 ) b · (1) c · (M · L −1 · T −1 )č · 

· (L 3 · T −1 ) d · (M · L −3 ) e · (T −1 ) f · (L) g = (2.3.58) 

= M a+č+e · L 2a+2b−č+3d−3e+g · T −3a−2b−č−d−f 


vrednosti eksponentov a, b, c, č in d ter izračunane vrednosti preostalih treh 

eksponentov po že znanem načinu. 

Karakteristična brezdimenzijska števila Π 1 , Π 2 , Π 3 , Π 4 , Π 5 in Π 6 , ki opisujejo delovanje 

hidravličnih turbinskih strojev, so tako določena: 

Π 1 = (P ) a · (gH) b · (η) c · (νϱ)č · ( ˙V ) d · (ϱ) e · (n) f · (d) g = 

P 

= 

ϱ · n 3 · d 5 (2.3.59) 

Brezdimenzijsko število Π 1 je poznano kot močnostno število. 


gH 

= 

n 2 · d 2 (2.3.60) 

Brezdimenzijsko število Π 2 je poznano kot energijsko število. 


= η (2.3.61) 

Brezdimenzijsko število Π 3 je preprosto izkoristek turbinskega stroja. 


νϱ 

= 

ϱ · n · d 2 = ν 

(n · d) · d = 1 

(2.3.62) 

Re u


Brezdimenzijsko število Π 4 je obratno sorazmerno z obodnim Reynoldsovim številom 

(indeks u). Izkazalo se je, da je tok v hidravličnih turbinskih strojih vedno močno 

turbulenten, zato viskoznost tekočine ne vpliva bistveno na delovanje stroja. Obodno 

Reynoldsovo število lahko v večini tehničnih primerov zanemarimo. 


˙V 

= 

n · d 3 (2.3.63) 

Brezdimenzijsko število Π 5 je poznano kot pretočno število. 

Karakteristika hidravličnih turbinskih strojev je podana kot funkcija štirih brezdimenzijskih 

števil: 

F 

( 

P 

ϱ · n 3 · d 5 , 

gH 

n 2 · d 2 , η, 

) 

˙V 

n · d 3 = 0 (2.3.64) 

Karakteristike hidravličnih turbinskih strojev so navadno prikazane kot funkcijska 

odvisnost pretočnega števila od močnostnega in energijskega števila ter od izkoristka 

turbinskega stroja: 

P 

ϱ · n 3 · d 5 = F ∗ ( ˙V 

n · d 3 ) 

gH 

n 2 · d 2 = F ∗∗ ( ˙V 

n · d 3 ) 

η = F ∗∗∗ ( ˙V 

n · d 3 ) 

(2.3.65) 

(2.3.66) 

(2.3.67) 

Zgled. Brezdimenzijske karakteristike toplotnih turbinskih strojev 

V preglednici 2.15 so podane najvažnejše fizikalne veličine, ki vplivajo na delovanje 

toplotnih turbinskih strojev, kot so turbinski kompresorji, parne in plinske turbine. 

Tudi pri toplotnih turbinskih strojih je – enako kot pri hidravličnih strojih – 

tok skozi stroj močno turbulenten, zato viskoznost tekočine ne vpliva bistveno na 

delovanje stroja. Obodno Reynoldsovo število lahko zanemarimo. Nasprotno od 

hidravličnih turbinskih strojev moramo pri toplotnih turbinskih strojih upoštevati stisljivost 

tekočine: volumenski tok je potrebno nadomestiti z masnim. Pri dimenzijski 

analizi je temperaturo primerno zapisati kot zmnožek plinske konstante s temperaturo 

(R T ), da se izognemo pisanju mere za temperaturo Θ.


Tabela 2.15: Fizikalne veličine za toplotne turbinske stroje 

Fizikalna Masni Vrtilna Izstopni Izstopna Eksponent Premer Vstopni Vstopna 

veličina tok frekv. tlak temperatura izentrope rotorja tlak temperatura 

Eksponent a b c č d e f g 

Oznaka ṁ n p 2 R T 2 κ d p 1 R T 1 

Mera M · T −1 T −1 M · L −1 · T −2 L 2 · T −2 - L M · L −1 · T −2 L 2 · T −2 

Karakteristika toplotnega turbinskega stroja je podana kot funkcija osmih spremenljivk 

n = 8: 

f(ṁ, n, p 2 , RT 2 , κ, d, p 1 , RT 1 ) = 0 (2.3.68) 

Število mer obravnavanega primera je i = 3, primer lahko zato zapišemo kot funkcijo 

petih brezdimenzijskih števil m = n − i = 5: 

F (Π 1 , Π 2 , Π 3 , Π 4 , Π 5 ) = 0 (2.3.69) 


Π . = (M · T −1 ) a · (T −1 ) b · (M · L −1 · T −2 ) c · (L 2 · T −2 )č · 

· (1) d · (L) e · (M · L −1 · T −2 ) f · (L 2 · T −2 ) g = (2.3.70) 

= M a+c+f · L −c+2č+e−f+2g · T −a−b−2c−2č−2f−2g 

Tabela 2.16: Matriki izbranih in izračunanih eksponentov za toplotne turbinske stroje 


a b c č d 

Π 1 1 0 0 0 0 

Π 2 0 1 0 0 0 

Π 3 0 0 1 0 0 

Π 4 0 0 0 1 0 

Π 5 0 0 0 0 1 


e f g 

Π 1 −2 −1 0,5 

Π 2 1 0 −0,5 

Π 3 0 −1 0 

Π 4 0 0 −1 

Π 5 0 0 0



vrednosti eksponentov a, b, c, č in d ter izračunane vrednosti preostalih treh eksponentov 

po že znanem načinu. 

Karakteristična brezdimenzijska števila Π 1 , Π 2 , Π 3 , Π 4 in Π 5 , ki opisujejo delovanje 

toplotnih turbinskih strojev, so tako določena: 

Π 1 = (ṁ) a · (n) b · (p 2 ) c · (RT 2 )č · (κ) d · (d) e · (p 1 ) f · (RT 1 ) g = 

= ṁ · √RT 

1 

p 1 · d 2 (2.3.71) 

Brezdimenzijsko število Π 1 je poznano kot pretočno število. 


= n · d √ RT1 

(2.3.72) 

Brezdimenzijsko število Π 2 je poznano kot brezdimenzijska vrtilna frekvenca. 


= p 2 

p 1 

(2.3.73) 

Brezdimenzijsko število Π 3 pomeni povečanje (zmanjšanje) tlaka pri kompresiji (ekspanziji) 

v kompresorju (turbini) med vstopom in izstopom turbinskega stroja in je 

primerljivo z energijskim številom pri hidravličnih turbinskih strojih. 


= RT 2 

RT 1 

= T 2 

T 1 

(2.3.74) 

Brezdimenzijsko število Π 4 pomeni povečanje (zmanjšanje) temperature pri kompresiji 

(ekspanziji) v kompresorju (turbini) med vstopom in izstopom turbinskega stroja 

in je, fizikalno gledano, povezano z notranjim izkoristkom turbinskega stroja. 


= κ (2.3.75) 

Brezdimenzijsko število Π 5 je preprosto eksponent izentrope. Karakteristika toplotnega 

turbinskega stroja je podana kot funkcija petih brezdimenzijskih števil: 

(ṁ √ · RT1 n · d 

F 

p 1 · d 2 , √ , p 2 

, T ) 

2 

, κ = 0 (2.3.76) 

RT1 p 1 T 1


Karakteristike toplotnih turbinskih strojev so navadno prikazane kot funkcijska odvisnost 

pretočnega števila od brezdimenzijske vrtilne frekvence, razmerja tlakov in 

temperatur ter od eksponenta izentrope. 

(ṁ √ ) 

n · d 

· R 

√ = F ∗ T1 

R T1 p 1 · d 2 (2.3.77) 

(ṁ √ ) 

p 2 

· R 

= F ∗∗ T1 

p 1 p 1 · d 2 (2.3.78) 

(ṁ √ ) 

T 2 

· R 

= F ∗∗∗ T1 

T 1 p 1 · d 2 (2.3.79) 

(ṁ √ ) 

· R 

η = F ∗∗∗ T1 

p 1 · d 2 (2.3.80) 

(ṁ √ ) 

· R 

κ = F ∗∗∗∗ T1 

p 1 · d 2 (2.3.81) 

Pretočno število je odvisno od razmerja temperatur, mogoče pa je dokazati, da lahko 

razmerje temperatur nadomestimo z izkoristkom. Pri večini praktičnih primerov je 

odvisnost pretočnega števila od eksponenta izentrope majhna in je navadno vsebovana 

v izkoristku.

Teoretične osnove

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?