Otázky ke II. části písemné zkoušky

Otázky ke II. části písemné zkoušky
Úvod do operačního výzkumu
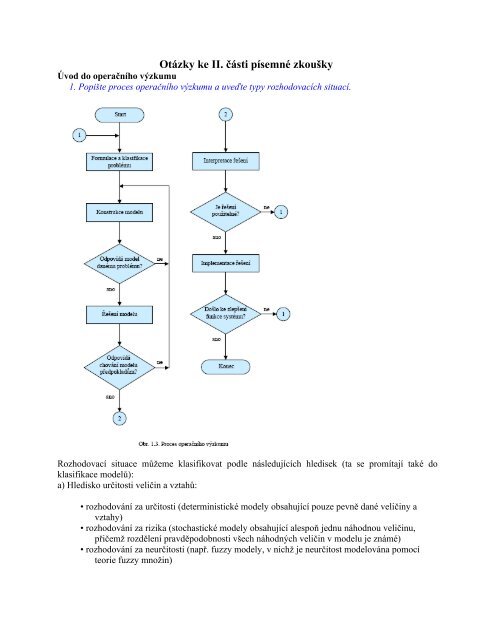
1. Popište proces operačního výzkumu a uveďte typy rozhodovacích situací.
Rozhodovací situace můžeme klasifikovat podle následujících hledisek (ta se promítají také do
klasifikace modelů):
a) Hledisko určitosti veličin a vztahů:
• rozhodování za určitosti (deterministické modely obsahující pouze pevně dané veličiny a
vztahy)
• rozhodování za rizika (stochastické modely obsahující alespoň jednu náhodnou veličinu,
přičemž rozdělení pravděpodobnosti všech náhodných veličin v modelu je známé)
• rozhodování za neurčitosti (např. fuzzy modely, v nichž je neurčitost modelována pomocí
teorie fuzzy množin)

) Hledisko počtu kritérií:
• rozhodování s jedním kritériem (jednokriteriální modely)
• rozhodování s více kritérii (vícekriteriální modely): např. při nákupu nějakého zařízení
můžeme chtít takové, které má co nejmenší cenu a současně co největší spolehlivost nebo
výkon
c) Hledisko počtu rozhodovatelů
• rozhodování s jedním rozhodovatelem: to ovšem nemusí být pouze jedna osoba, ale může to
být i skupina osob, majících stejné cíle (např. vedení podniku)
• rozhodování s více rozhodovateli: používají se pro modelování konfliktních situací (např. na
trhu se v konkurenčním boji střetávají zájmy různých rozhodovatelů) a zabývá se jimi
teorie her
2. Na zvoleném příkladě popište strukturu optimalizačního modelu.
Při výběru veličin je nutné zvážit otázku úrovně podrobnosti modelu, která by měla odpovídat jednak
účelu modelování, jednak kvalitě dostupných informací o zkoumaném objektu.
Veličiny modelu vstupují do následujících matematických vztahů:
• kriteriální (účelová) funkce, vyjadřující závislost zvoleného kritéria na neřiditelných
veličinách a rozhodovacích proměnných; tato funkce může být maximalizačního (např.
zisk, hodnota produkce, spolehlivost) nebo minimalizačního typu (např. náklady);
• omezující podmínky které vymezují množinu přípustných řešení modelu; jsou to rovnice nebo
nerovnice, v nichž vystupují rozhodovací proměnné a neřiditelné veličiny; tyto podmínky
dělíme na
• vlastní omezení (zachycují vztahy, které musejí platit mezi rozhodovacími
proměnnými),
• podmínky pro jednotlivé rozhodovací proměnné (např. dolní a horní meze hodnot
těchto proměnných nebo podmínky jejich celočíselnosti).

Formulace a vlastnosti úloh lineárního programování
3. Napište definici báze. Ilustrujte na příkladě. Jaký je maximální počet různých bází?
Nechť A je typu (m, n) o hodnosti m a nechť B je matice tvořená m lineárně nezávislými sloupci
matice A. Pak matice B se nazývá bází uvedené úlohy LP. Každá báze určuje právě jedno bázické
řešení.
Proměnné odpovídající sloupcům matice B se nazývají bázické. Ostatní proměnné se nazývají
nebázické. Počet různých bází a tedy i počet různých bázických řešení je shora ohraničen
⎛ n ⎞
kombinačním číslem ⎜ ⎟ a je tedy konečný.
⎝ m ⎠
4. Napište definici bázického řešení. Ilustrujte na příkladě. Jaký je geometrický význam bázického
řešení?
Řešení soustavy Ax = b se nazývá bázické, jestliže sloupce matice A, které odpovídají nenulovým
složkám tohoto řešení, tvoří lineárně nezávislou soustavu vektorů.
Přípustné bázické řešení je takové bázické řešení, které navíc vyhovuje podmínkám nezápornosti
x ≥ 0.
Přípustné řešení úlohy LP je bázické právě tehdy, je-li krajním bodem množiny přípustných
řešení.
5. Jak se zjistí bázické řešení odpovídající dané bázi B? Ilustrujte na příkladě.
Bázické řešení pro danou bázi můžeme získat následovně. Nechť B je báze úlohy (2.11). Označme
x B … vektor bázických proměnných
x N … vektor nebázických proměnných
Položme nebázické proměnné rovny nule, tj. x N = 0. Pak vektor x B je řešením rovnice Bx B = b a tedy
x B = B –1 b
6. Jak zní základní věta LP a co je jejím důsledkem?
Pro úlohu LP
max{c T x| Ax=b, x>=0}
může nastat právě jedna z těchto tří možností:
a) množina přípustných řešení M = ∅ (úloha LP nemá žádné přípustné řešení),
b) M ≠ ∅ a množina optimálních řešení M * = ∅ (úloha LP má přípustné řešení, ale nemá žádné
optimální řešení),
c) M * ≠ ∅ (úloha LP má optimální řešení).
Dále platí:
Je-li M ≠ ∅, pak existuje přípustné bázické řešení.

Je-li M * ≠ ∅, pak existuje bázické optimální řešení.
Tedy jestliže má úloha LP přípustné řešení, má také přípustné bázické řešení a jestliže má
optimální řešení, má také bázické optimální řešení.
Význam základní věty LP spočívá v tom, že v jejím důsledku se při hledání optimálního řešení úlohy
LP se můžeme omezit pouze na řešení bázická, jejichž počet je konečný. Základní věta LP je
teoretickým základem simplexové metody řešení úloh LP.
Simplexová metoda
7. Popište dvoufázovou simplexovou metodu.
Do původní úlohy zavedeme nezáporné pomocné (umělé) proměnné tak, abychom získali
kanonický tvar, a původní účelovou funkci nahradíme pomocnou účelovou funkcí, která je
součtem pomocných proměnných. V prvé fázi simplexové metody pak simplexovým algoritmem
hledáme bázické řešení, které minimalizuje pomocnou účelovou funkci. Pokud jsou v tomto
řešení všechny pomocné proměnné nulové, použijeme hodnoty ostatních proměnných jako
výchozí pro druhou fázi simplexové metody, v níž pomocí simplexového algoritmu hledáme
bázické řešení, které optimalizuje původní účelovou funkci. Jestliže se při minimalizaci pomocné
účelové funkce nepodařilo anulovat všechny pomocné proměnné, pak to znamená, že původní
úloha nemá žádné přípustné řešení.
a) Je-li g(x Po ) = 0 (tj. jestliže jsou všechny pomocné proměnné rovny nule), pak vektor x o je výchozí
přípustné bázické řešení původní úlohy.
b) Je-li g(x Po ) ≠ 0, pak původní úloha nemá žádné přípustné řešení. Poznamenejme, že v takovém
případě musí být hodnota pomocné účelové funkce kladná, protože tato funkce je součtem
nezáporných pomocných proměnných. Pokud by tedy tato hodnota vyšla záporná, znamenalo by
to, že při výpočtu došlo k nějaké chybě.
Obecně má simplexová metoda dvě fáze (proto se používá název dvoufázová simplexová metoda):
1. Nalezení výchozího přípustného bázického řešení.
Jestliže úloha nemá žádné přípustné řešení, pak postup končí. V opačném případě se přechází na
druhou fázi.
2. Hledání optimálního bázického řešení.
Tato fáze končí nalezením optimálního bázického řešení nebo zjištěním, že optimální řešení
neexistuje.
V obou fázích se využívá simplexový algoritmus, který bude popsán v následujícím odstavci.

Simplexový algoritmus
Mějme výchozí přípustné bázické řešení x 1 . Položme k = 1, A (k) = A, b (k) = b. Simplexový algoritmus
sestává z následujících tří kroků, které později rozvedeme podrobněji:
1. Test kritéria optimality pro x k . Je-li splněno, pak konec (bázické řešení x k je optimálním řešením).
2. Určení klíčového prvku a matice A)(krs (k) . Není-li možné určit klíčový prvek, pak konec (úloha
nemá konečné optimální řešení).
3. Simplexová transformace matice (A (k) | b (k) ). Získáme matici (A (k+1) | b (k+1) ) a nové bázické řešení
x k+1 . Položíme k = k + 1 a postup opakujeme od bodu 1.
8. Jaké jsou možné případy zakončení simplexové metody? Ilustrujte graficky. Jak se tyto případy
poznají v simplexové tabulce?
Podle základní věty LP (viz § 2.3) mohou pro každou úlohu LP nastat pouze tři možnosti: má
optimální řešení, má přípustné ale nemá optimální řešení, nemá přípustné řešení. V následujícím
přehledu prvý případ rozdělíme na dva podpřípady a uvedeme, jak se tyto situace poznají v
simplexové tabulce:
1. Úloha má jediné optimální řešení:
Je splněno kritérium optimality a pro všechny nebázické proměnné jsou redukované ceny Δ j ≠ 0.
2. Úloha má nekonečně mnoho optimálních řešení:
Je splněno kritérium optimality a alespoň pro jednu nebázickou proměnnou je redukovaná cena Δ j =
0.
3. Úloha nemá konečné optimální řešení:
Není splněno kritérium optimality a není možno určit klíčový řádek.
4. Úloha nemá žádné přípustné řešení:
Optimální hodnota pomocné účelové funkce není nulová.
Tyto možnosti zakončení simplexové metody se vztahují k případu, kdy úloha není degenerovaná.
Degenerovaná je taková úloha, která má alespoň jedno degenerované bázické řešení.
U degenerované úlohy mohou nastat tyto situace:
• výskyt Δ j = 0 u nebázické proměnné nemusí být příznakem existence nekonečně mnoha
optimálních řešení (viz příklad 3.11),
• může dojít k zacyklení (toto nebezpečí se dá odstranit úpravou simplexového algoritmu).

Dualita a analýza citlivosti
9. Napište definici dvojice symetricky duálně sdružených úloh a uveďte konkrétní příklad takové
dvojice.
Přitom maximalizační úloze odpovídá úloha minimalizační a naopak. Úlohy lineárního
programování se tedy vlastně vyskytují ve dvojicích (hovoříme o dvojicích duálně sdružených
úloh). Původní úlohu v této dvojici nazýváme primární, kdežto úlohu s ní sdruženou označujeme
jako duální.
10. Napište slabou a silnou větu o dualitě. Jaké jsou důsledky těchto vět?
Slabá věta o dualitě
Nechť primární úloha je maximalizační s účelovou funkcí f(x), duální úloha je minimalizační s
účelovou funkcí g(u), a nechť x 0 je libovolné přípustné řešení primární úlohy a u 0 je libovolné
přípustné řešení duální úlohy. Pak platí
f(x 0 ) ≤ g(u 0 )
Tedy hodnota účelové funkce minimalizační úlohy v kterémkoli přípustném řešení je horní mezí
hodnot účelové funkce duálně sdružené maximalizační úlohy na množině všech jejích přípustných
řešení a obdobně hodnota účelové funkce maximalizační úlohy v kterémkoli přípustném řešení je
dolní mezí hodnot účelové funkce duálně sdružené minimalizační úlohy na množině všech jejích
přípustných řešení.
Silná věta o dualitě
Má-li jedna z duálně sdružených úloh optimální řešení, má optimální řešení i úloha druhá, přičemž
optimální hodnoty účelových funkcí jsou si rovny.
Důsledky silné a slabé věty o dualitě
• Platí-li pro přípustné řešení x 0 primární úlohy a pro přípustné řešení u 0 duální úlohy rovnost f(x 0 )
= g(u 0 ), pak x 0 a u 0 jsou optimální řešení.
• Je-li množina přípustných řešení maximalizační úlohy neprázdná a je-li účelová funkce této úlohy
shora neomezená, pak duálně sdružená úloha nemá žádné přípustné řešení.
• Je-li množina přípustných řešení minimalizační úlohy neprázdná a je-li účelová funkce této úlohy
zdola neomezená, pak duálně sdružená úloha nemá žádné přípustné řešení.
• Nemá-li jedna z dvojice duálně sdružených úloh přípustné řešení, pak druhá úloha nemá
optimální řešení.

Prvá tři tvrzení jsou důsledkem slabé věty o dualitě, zatímco poslední tvrzení lze chápat jako
důsledek silné věty o dualitě.
11. Napište větu o komplementaritě. Na jejím základě odpovězte na otázku, jaká bude v úloze
optimalizace výrobního programu optimální hodnota duální proměnné, když odpovídající zdroj
nebude plně využit?
Přípustná řešení symetricky duálně sdružených úloh jsou optimální právě tehdy, když platí
Toto tvrzení je sice pro jednoduchost zformulováno pro případ symetricky duálně sdružených úloh,
ale platí i v nesymetrických případech. Výše uvedené vztahy znamenají, že nabývá-li nějaká
proměnná kladnou hodnotu, pak odpovídající duálně sdružené omezení musí být splněno jako rovnice
(tj. příslušná doplňková proměnná musí být nulová) a naopak je-li nějaké omezení splněno jako ostrá
nerovnost (tj. příslušná doplňková proměnná je nenulová), pak odpovídající duálně sdružená
proměnná musí být nulová. Jak uvidíme dále, tato věta má zajímavou ekonomickou interpretaci.
- nulová.
12. Co je cílem analýzy citlivosti a jaké úlohy se zde řeší? Jaký je význam duálních proměnných z
hlediska analýzy citlivosti?
Dodatečně pak chceme zjistit, zda to, co jsme vynechali, skutečně nemá na optimální řešení vliv.
Rovněž koeficienty v zadání úlohy se často mohou měnit nebo mohou být pouhými odhady a
potřebujeme zjistit, jak případné změny těchto koeficientů ovlivňují optimální řešení úlohy.
Těmito otázkami se zabývá analýza citlivosti, která také bývá nazývána postoptimalizační
analýzou. Někdy lze popsat změnu zadání úlohy jako závislost koeficientů úlohy na parametrech,
které nabývají hodnot z dané množiny. Sledujeme pak závislost optimálního řešení na těchto
parametrech a hovoříme o úloze parametrického programování.
K analýze citlivosti optimálního řešení na změny zadání úlohy existují dva základní přístupy.
Optimální hodnoty duálních proměnných vyjadřují citlivost optimální hodnoty primární účelové
funkce na změny pravých stran primárních omezení. Duální proměnné tudíž hrají důležitou roli v
analýze citlivosti.
Optimální hodnoty duálních proměnných zde tedy představují
ocenění zdrojů z hlediska jejich omezenosti a proto se také nazývají stínovými cenami. Tyto
ceny mohou podnikovému managementu pomoci rozhodnout, zda zvýšit výrobu dodatečným
získáním omezených zdrojů. Jestliže stínová cena jednotky některého zdroje není vyšší než cena,

kterou by bylo nutno vynaložit na dodatečné získání jednotky tohoto zdroje, tak se nevyplatí
zásobu tohoto zdroje zvyšovat.
Nelineární programování
13. Napište definice konvexní funkce a konvexní množiny. Nakreslete příklady konvexních a
nekonvexních funkcí a množin.
Nechť funkce f(x) je definována na konvexní množině K. Řekneme, že f(x) je konvexní funkcí na
K právě tehdy, když pro každé dva body x 1 , x 2 K a libovolné t (0;1) platí
Jestliže pro každé dva body x 1 , x 2 K , x 1 ≠ x 2 platí ostrá nerovnost, řekneme, že funkce f(x) je na
množině K ryze konvexní. Geometricky vztah (5.5) znamená, že graf funkce leží pod sečnou spojující
body (x 1 ; f(x 1 )) a (x 2 ; f(x 2 )).
Konvexní množina
Podmnožinu K vektorového prostoru V nazveme konvexní množinou, jestliže s libovolnými dvěma
body x 1 K, x 2 K leží v této množině také všechny body
x =t x 1 + (1– t) x 2
kde 0 < t < 1. Geometricky to znamená, že množina K spolu s libovolnými dvěma různými body
musí obsahovat i úsečku spojující tyto dva body (viz obr. 2.3).

14. Zvolte si nějakou nelineární funkci více proměnných a určete její gradient. Jaké jsou vlastnosti
gradientu?
Gradient
Nechť funkce f(x) má v bodě x 0 parciální derivace 1. řádu. Gradientem funkce f(x) v bodě x 0
nazýváme vektor
Gradient má následující vlastnosti:
• Gradient f(x 0 ) je kolmý na hladinovou nadplochu f(x) = f(x 0 ) v bodě x 0 .
• Gradient f(x 0 ) ukazuje směr, ve kterém funkce f(x) v okolí bodu x 0 nejrychleji roste (směr
největšího růstu). Směr největšího spádu ukazuje obrácený gradient – f(x 0 ).
• Nechť M = { x | g i (x) ≤ 0 } a nechť pro x 0 M platí g i (x 0 ) = 0. Pak gradient g i (x 0 ) je kolmý k
nadploše g i (x 0 ) = 0 a směřuje ven z množiny M.
• Nechť bod x min M lokálního minima funkce f(x) na množině M je hraničním bodem množiny
M. Pak gradient f(x min ) směřuje dovnitř množiny M.

15. Zvolte si nějakou nelineární funkci více proměnných a určete Hessovu matici této funkce. K
čemu používáme Hessovu matici? Ilustrujte to na zvolené funkci.
Hessova matice
Nechť funkce f(x) má v bodě x 0 parciální derivace 2. řádu. Hessovou maticí v bodě x 0 nazýváme
matici
Jestliže funkce f(x) má spojité druhé parciální derivace, pak Hessova matice je symetrická.
Jak již bylo uvedeno v odstavci věnovaném konvexním funkcím, Hessova matice je pomůckou pro
ověřování konvexnosti funkcí. Nechť funkce f(x) je definována na konvexní množině M a má zde
spojité parciální derivace 2. řádu. Pak funkce f(x) je
• • konvexní na množině M, jestliže pro všechna x M je Hessova matice pozitivně
semidefinitní,
• • ryze konvexní na množině M, jestliže pro všechna x M je Hessova matice pozitivně
definitní (s případnou výjimkou množiny míry nula, kde je pozitivně semidefinitní).
16. Napište definici úlohy konvexního programování. Jaké má tato úloha vlastnosti?
Řekneme, že úloha
je úlohou konvexního programování právě tehdy, když M je konvexní množina a funkce f(x) je
konvexní na M. Příklady takových úloh ukazují obrázky 5.1 a 5.2. Následující tvrzení umožňuje
rozhodnout, zda je konvexní množina, která je dána nějakými omezujícími podmínkami.
Nechť
Pak množina M je konvexní, jestliže množina X je konvexní a všechny funkce g i (x) jsou konvexní na
X. Poznamenejme, že pokud by se mezi omezujícími podmínkami vyskytla rovnice, pak tato rovnice
musí být lineární.
Vlastnosti úlohy konvexního programování:
• každé lokálně optimální řešení je globálně optimálním řešením,
• je-li množina optimálních řešení neprázdná, je konvexní,
• je-li f(x) ryze konvexní, má úloha nejvýše jedno optimální řešení.
17. Jaké znáte typy metod jednorozměrné optimalizace? Jak mohou být využity ve vícerozměrné
optimalizaci?
• Metody bez použití derivace: Interval zužujeme na základě porovnání hodnot funkce ve dvou
vnitřních bodech x 1 , x 2 , x 1 < x 2 (metoda zlatého řezu, Fibonacciho metoda). Je-li ϕ(x 1 ) < ϕ(x 2 ),

pak interval redukujeme na interval . Je-li ϕ(x 1 ) > ϕ(x 2 ), je výsledkem redukce
interval .
• Metody s použitím derivací: V metodě půlení intervalu se interval redukuje na základě
znaménka 1. derivace ve středu s intervalu . Je-li ϕ´(s) > 0, je výsledkem redukce interval
. Je-li ϕ´(s) < 0, je to interval . Newtonova metoda využívá 2. derivaci pro hledání
kořene rovnice ϕ´(λ) = 0.
• Metody založené na aproximaci: V každém iteračním kroku se provádí kvadratická nebo
kubická interpolace funkce ϕ .
18. Charakterizujte obecný princip vícerozměrných metod hledání volných extrémů funkce více
proměnných. Jak se dá určit směr přechodu k dalšímu řešení?

19. Charakterizujte typy metod pro hledání vázaných extrémů funkce více proměnných.
Metody hledání vázaných extrémů
Metody pro hledání vázaných extrémů můžeme rozdělit do těchto skupin:
• Metody založené na transformaci úlohy hledání vázaného extrému na úlohu hledání volného
extrému:
• − penalizační a bariérové metody
• − metoda využívající Lagrangeovu funkci rozšířenou o kvadratický penalizační člen
• Linearizační metody:
• − metody spočívající v řešení posloupnosti úloh LP, aproximujících danou úlohu NLP
• − metody výběru směru založené na linearizaci
• Metody řešení speciálních úloh:
• − metody kvadratického programování
• − metody separovatelného programování
Celočíselné programování
20. Charakterizujte princip metody sečných nadrovin.
Metody sečných nadrovin
Pro metody sečných nadrovin (metody řezů) je charakteristická počáteční úprava dané celočíselné
úlohy, která spočívá ve „vnoření“ množiny přípustných řešení do nějaké souvislé nadmnožiny (jinými
slovy jde o dočasné zanedbání podmínek celočíselnosti). Na takto získanou spojitou úlohu se pak
aplikuje nějaká vhodná optimalizační metoda. Jestliže optimální řešení upravené úlohy vyhovuje
požadovaným podmínkám celočíselnosti, je vyřešena i původní úloha. V opačném případě se do
spojité úlohy doplní dodatečné lineární omezení, které má tyto vlastnosti:
• není splněno pro optimální neceločíselné řešení,
• je splněno pro libovolné přípustné řešení původního celočíselného problému.
Přidání tohoto omezení odpovídá geometricky zavedení nadroviny, která od množiny přípustných
řešení spojitého problému „odřízne“ optimální neceločíselné řešení, přičemž nedojde ke ztrátě
žádného přípustného řešení celočíselného problému. Postup se opakuje, tj. doplněný spojitý problém
se znovu řeší a splňuje-li získané optimální řešení podmínky celočíselnosti, je výpočet ukončen,
kdežto v opačném případě se přidá další omezení atd.

Původně byly metody sečných nadrovin konstruovány pouze pro lineární úlohy. Z nich
nejznámější jsou Gomoryho metody. Později došlo k rozvoji těchto metod ve směru jejich
rozšíření na některé obecnější úlohy. Použití metod sečných nadrovin může v některých
případech narazit na problémy spojené s nadměrným růstem rozměrnosti úlohy při přidávání
dodatečných omezení a s pomalou konvergencí.
Postup řešení celočíselné úlohy LP (6.11) – (6.14) může být tedy popsán takto:
1. Úlohu (6.11) – (6.13) řešíme simplexovou metodou. Splňuje-li získané optimální řešení podmínky
celočíselnosti, pak postup končí. V opačném případě položíme s = 1 a pokračujeme bodem 2.
2. K soustavě rovnic z poslední simplexové tabulky připojíme rovnici:
kde k je určeno vztahem R k = max R i a proměnná x n+s je vázána podmínkou nezápornosti.
3. V rozšířené simplexové tabulce považujeme nově připojený řádek za klíčový a řešíme ji dále
duálně simplexovou metodou. Jestliže je optimální řešení celočíselné, postup končí. V opačném
případě zvětšíme s o jedničku a postup opakujeme od bodu 2.
K popsané metodě řezů ještě na závěr poznamenejme, že růstu rozměrnosti rozšířené úlohy
můžeme zabránit tím, že po vyloučení dodatečné proměnné x n+s z báze vypustíme z řešené
soustavy i příslušné dodatečné omezení.
21. Charakterizujte princip metody větví a mezí a uveďte příklady způsobů větvení a omezování.
Metoda větví a mezí
Metoda větví a mezí (branch and bound) je iterační metoda pro nalezení globálního extrému funkce
f(x) na množině přípustných řešení M. Tato metoda je založena na opakování následujících dvou
operací:
• větvení, při němž se zprvu množina M a později její vybraná podmnožina rozkládá na po dvou
disjunktní podmnožiny (postup rozkladu množiny M je možno znázornit stromovým grafem,
jehož uzly odpovídají jednotlivým podmnožinám),
• omezování, při němž se pro každou podmnožinu získanou předchozí operací určuje dolní (při
minimalizaci) resp. horní (při maximalizaci) mez hodnot funkce f(x) na této podmnožině.
Pro další rozklad se volí podmnožina s nejnižší dolní resp. nejvyšší horní mezí. Cílem je najít takové
přípustné řešení, pro něž hodnota účelové funkce není větší než dolní meze resp. není menší než horní
meze u všech dosud nerozložených podmnožin, neboť takové řešení je optimální.
Všimněme si, že v popisu metody větví a mezí se vůbec neobjevila zmínka o celočíselnosti
proměnných. Znamená to, že použitelnost metody není omezena pouze na úlohy celočíselného
programování.

Metoda větví a mezí je vhodná pro řešení úloh, ve kterých struktura množiny M umožňuje
jednoduchý postup rozkladu a funkce f(x) dovoluje odvodit příslušné dolní nebo horní meze.
Efektivnost postupu závisí na stanovení mezí h(M k ). Příliš hrubé meze mohou způsobit to, že se strom
úlohy příliš „rozroste“. Přesnější meze sice vedou k redukci stromu úlohy, ale z toho plynoucí úspora
může být na druhé straně negována náročností výpočtu těchto mezí. Obecně mohou být meze hodnot
účelové funkce určeny pomocí nějaké heuristické metody. V případě, že metodu větví a mezí
aplikujeme na problém celočíselného programování, je možno příslušné meze získat zanedbáním
podmínek celočíselnosti a použitím nějaké metody „neceločíselné“ optimalizace.
Úlohy síťové optimalizace
22. Napište definici orientovaného grafu a nakreslete příklad. Jaké znáte typy grafů? Uveďte
příklady aplikací.
Orientovaný graf je definován jako dvojice
kde V je množina vrcholů (uzlů) a E je množina orientovaných hran, definovaná jako
podmnožina kartézského součinu V × V, tj.
Orientovaná hrana je tedy uspořádaná dvojice vrcholů e = (v1, v2), kde v1 je počáteční uzel a v2 je
koncový uzel. Příklad orientovaného grafu je ukázán na obr. 7.1, kde kroužky představují vrcholy a
orientované spojnice reprezentují hrany.
Pomocí orientovaného grafu může být modelován např. výrobní systém, kde stroje jsou
reprezentovány pomocí uzlů a orientované hrany odpovídají tokům materiálu, polotovarů a
výrobků. Jiným příkladem je model kanalizační sítě kde hrany představují úseky potrubí
(orientace je dána spádem) a vrcholy odpovídají vpustím a spojovacím uzlům.

Kromě orientovaných grafů ještě existují neorientované a smíšené grafy. Neorientovaný graf je
definován jako dvojice (7.1), kde
přičemž symbol (V nad 2) označuje množinu všech dvouprvkových podmnožin množiny V. Tedy
každá neorientovaná hrana je množina obsahující dva vrcholy, e = {v1, v2}. Neorientovaný graf může
být např. modelem automapy, kde vrcholy jsou obce a hrany jsou úseky silnic mezi obcemi.
Smíšený graf je definován jako dvojice (7.1), kde
Pomocí smíšeného grafu můžeme zobrazit např. síť ulic ve městě, kde vrcholy odpovídají náměstím,
křižovatkám a začátkům a koncům ulic, neorientované hrany představují obousměrné ulice a
orientované hrany ulice jednosměrné.
V dalších podkapitolách se budeme zabývat pouze orientovanými grafy. Neorientované a smíšené
grafy můžeme převést na orientované tak, že každou neorientovanou hranu nahradíme dvojicí
opačně orientovaných hran (viz obr 4.2).

23. Jak je definován tok od zdroje ke spotřebiči? Ilustrujte na příkladě. Charakterizujte možné
způsoby nalezení maximálního toku (stačí slovně).
Podmínka (7.13) říká, že tok hranou musí být nezáporný a nesmí překročit její kapacitu. Podmínka
(7.14) znamená, že pokud uzel není zdroj ani spotřebič, musí být součet toků do něj vstupujících
roven součtu toků z něj vystupujících.

Ford - Fulkersonův algoritmus vychází z nějakého přípustného toku a opakují se v něm dvě fáze. V
prvé fázi se hledá cesta ze zdroje do spotřebiče (bez ohledu na orientaci hran), pomocí níž je možno
tok zvýšit. Přitom se jistým způsobem označují uzly grafu. Ve druhé fázi se na nalezené cestě
provádějí změny toku (na hranách orientovaných směrem ke spotřebiči se tok zvyšuje a na opačně
orientovaných hranách se snižuje). Pokud v prvé fázi nelze požadovanou cestu najít, algoritmus
končí, přičemž množina označených uzlů a množina neoznačených uzlů určují minimální řez.
24. Vysvětlete pojmy cesta a vzdálenost v orientovaném hranově ohodnoceném grafu. Ilustrujte na
příkladě. Charakterizujte možné způsoby nalezení nejkratší cesty (stačí slovně).
Cesta je sled, ve kterém se neopakuje žádný uzel.
Orientovaná cesta je cesta, v níž všechny hrany mají shodnou orientaci.

Jedná se o úlohu lineárního bivalentního (nula-jedničkového) programování. Jestliže nahradíme
podmínky xij ∈ {0, 1} podmínkami nezápornosti a prvou rovnici vynásobíme (–1), dostáváme
následující úlohu normálního lineárního programování.

Složité rozhodovací úlohy
25. Charakterizujte úlohu dynamického programování a naznačte způsob jejího řešení. Uveďte
příklady aplikací.
Dynamické programování se zabývá optimalizací dynamických úloh, které je možno formulovat také
jako úlohy řízení procesů probíhajících v čase. Dynamické programování je však použitelné i pro
takové problémy, v nichž čas explicitně nevystupuje a může být do nich uměle zaveden.
Přístupy dynamického programování využívají aparát rekurentních funkcionálních vztahů a
opírají se přitom o tzv. princip optimality, jehož autorem je Richard Bellman. Aplikace těchto
přístupů vyžaduje zpravidla náročnější přípravu než aplikace metod matematického
programování, neboť neexistuje žádný dostatečně obecný algoritmus k řešení některé třídy
problémů dynamického programování. Tedy přístupy dynamického programování v sobě zahrnují
nejen vytvoření matematického modelu, ale také konstrukci výpočetní procedury k jeho řešení.
Získaný algoritmus přitom podstatně závisí na struktuře řešeného problému.
Příklady aplikací dynamického programování
• Plánování výroby a zásob. Je třeba pro každou etapu plánovacího období určit, jaké množství
výrobku vyrobit a jaké uskladnit pro budoucí použití, aby byla splněna poptávka po výrobku a
byly minimalizovány seřizovací, výrobní a skladovací náklady.
• Obnova zařízení. Zařízení postupně zastarává a zisk z jeho použití se postupně snižuje. Je třeba
určit, kdy je nevhodnější pořídit nové zařízení.
• Rozdělování zdrojů. Je dáno omezené množství nějakého ekonomického zdroje a několik
možných způsobů použití s různým přínosem. Je třeba dané množství rozdělit tak, aby byl
maximalizován celkový přínos.
26. Charakterizujte úlohu stochastického programování. Jaké jsou možnosti vytvoření
deterministického ekvivalentu této úlohy? Uveďte příklady aplikací.
Příklady aplikací stochastického programování
• Plánování výroby při neurčité poptávce. Je třeba pro každou etapu plánovacího období určit,
jaké množství výrobku vyrobit a jaké uskladnit pro budoucí použití, aby byly minimalizovány
náklady, přičemž poptávky po výrobku v jednotlivých obdobích jsou náhodné veličiny.

• Dopravní problém s neurčitou poptávkou. Je třeba určit takový plán přepravy, při němž budou
celkové náklady na přepravu minimální, přičemž dopravní náklady a kapacity dodavatelů jsou
konstantní, ale požadavky odběratelů jsou náhodné veličiny.
• Optimalizace portfolia. Je třeba stanovit skladbu portfolia cenných papírů tak, aby se
maximalizoval výnos portfolia, přičemž výnosy jednotlivých aktiv jsou náhodné veličiny.
Za řešení úlohy stochastického programování (8.15) se považuje řešení deterministického
ekvivalentu této úlohy, který je definován tak, aby byla z původní úlohy korektně odstraněna
náhodnost. Při konstrukci deterministického ekvivalentu je nutné stanovit, co budeme považovat
za přípustné řešení a co budeme považovat za optimální řešení.
Pokud musíme určit jednorázové řešení (rozhodnutí), které se po získání novějších informací
nemůže měnit, hovoříme o jednostupňových úlohách stochastického programování. Jestliže
řešení můžeme upravovat na základě postupně se objevujících nových informací, jde o
vícestupňové úlohy stochastického programování. Ve vícestupňových úlohách se proces
rozhodování může rozvíjet podle jednoho ze dvou následujících řetězců:

27. Charakterizujte úlohy vícekriteriálního rozhodování a uveďte příklady aplikací. Na příkladě
vysvětlete pojmy dominovaného a nedominovaného řešení.
Problém vícekriteriálního rozhodování lze charakterizovat takto: je dána nějaká množina možných
variant (rozhodnutí, řešení) a máme vybrat variantu, která je co možná nejlepší vzhledem k dané
množině kritérií (hledisek, charakteristik).
Typy kritérií
Kritéria uvažovaná ve vícekriteriálním rozhodování bývají obvykle konfliktní. Mohou se mezi nimi
vyskytnout jak kritéria kvantitativní (kardinální), tak kritéria kvalitativní (ordinální). V případě
současného výskytu kvalitativních i kvantitativních kritérií se provádí přechod k jednomu typu
kritérií, buď ke kvalitativním nebo ke kvantitativním.
Kvantitativní kritéria umožňují pro každou variantu stanovit hodnoty kritérií. Tato kritéria
bývají často nesouměřitelná v důsledku vyjádření v různých jednotkách. U některých metod pro
řešení vícekriteriálních úloh je třeba tuto nesouměřitelnost odstranit určitou normalizací (např.
přechodem k ukazatelům, které vyjadřují procenta plnění původních ukazatelů).
Kvalitativní kritéria dovolují pouze stanovit, zda je nějaká varianta podle určitého kritéria lepší či
horší než jiná, nebo zda jsou podle tohoto kritéria obě srovnávané varianty rovnocenné.
Příklady úloh vícekriteriálního rozhodování
• Výběr zařízení pro použití ve výrobě. Kritéria: cena, výkon, spolehlivost, provozní náklady.
• Výběr zakázek pro výrobu v daném období. Kritéria: velikost tržeb, procento pokrytí režie,
posílení pozice na trhu, udržení stavu zaměstnanců.
• Výběr projektu na výstavbu nějakého zařízení. Kritéria: investiční náklady, provozní náklady,
vliv na životní prostředí, možnost budoucího rozšíření.
• Hodnocení bonity bankovních klientů. Kritéria: finanční situace (zadluženost), vyrovnanost
potřeb a zdrojů, možnosti reprodukce firmy, efektivnost hospodaření firmy, ukazatele obratu.
Typy vícekriteriálních úloh:

Množina přípustných variant může být vymezena buď explicitně výčtem těchto variant, nebo
implicitně nějakou soustavou podmínek. Úlohy s explicitně vymezenými variantami nazýváme
úlohami vícekriteriálního hodnocení variant. Jsou-li přípustné varianty dány implicitně systémem
podmínek a všechna kritéria jsou kvantitativní, jedná se o úlohy vícekriteriálního programování
(úlohy vektorové optimalizace).
• Úlohy vícekriteriálního hodnocení variant (přípustné varianty jsou vymezeny explicitně).
• Úlohy vícekriteriálního programování (přípustné varianty jsou vymezeny implicitně soustavou
podmínek a všechna kritéria jsou kvantitativní).
Dominovaná a nedominovaná řešení
Je jasné, že jen velmi zřídka můžeme najít variantu, která by byla skutečně nejlepší z hlediska
každého zadaného kritéria, a že se tedy většinou musíme spokojit s nějakým kompromisem. Je
přirozené za kompromisní považovat takovou variantu, k níž neexistuje žádná varianta,která by
byla lepší alespoň v jednom kritériu a v žádném nebyla horší. Takto vymezená kompromisní varianta
se nazývá efektivní, nedominovaná nebo paretovsky optimální. Nedominovanost resp. paretovská
optimalita tedy znamená takový stav, kdy žádné kritérium nemůže být zlepšeno, aniž by došlo ke
zhoršení nějakého jiného kritéria.
28. Popište možnosti řešení úloh vícekriteriálního rozhodování.
Metody vícekriteriálního programování
Tyto metody jsou v podstatě založeny na jednorázovém nebo opakovaném použití metod
jednokriteriální optimalizace. Podle toho, zda a kdy jsou k dispozici nějaké doplňující informace o
rozhodovatelových preferencích, lze specifikovat následující případy:
• jsou k dispozici apriorní informace o preferencích rozhodovatele,
• doplňující informace o preferencích rozhodovatele jsou zadávány až v průběhu řešení úlohy
• žádné doplňující informace o preferencích rozhodovatele nejsou k dispozici
Jestliže jsou předem k dispozici informace o preferencích rozhodovatele, pak lze danou úlohu převést
na úlohu jednokriteriální optimalizace resp. na posloupnost takových úloh. Těmito informacemi
mohou být váhy kritérií, pořadí důležitosti kritérií nebo požadované (ideální) hodnoty kritérií. Podle
charakteru informací o preferencích rozhodovatele rozlišujeme tyto metody:
• metody agregace kritérií
• metody lexikografické optimalizace

• metody minimalizace vzdálenosti od ideálního vektoru
Jsou-li doplňující informace o preferencích rozhodovatele jsou zadávány až v průběhu řešení úlohy,
jedná o tzv. interaktivní metody, které spočívají na dialogu mezi rozhodovatelem a řešitelem (tím je
obvykle počítač), při nichž se střídají dvě fáze – fáze výpočetní a fáze rozhodovací. Výpočetní fáze je
prováděna řešitelem a jejím výstupem je jedno nebo více provizorních řešení úlohy a případně nějaké
další informace důležité pro rozhodovatele. Při výpočtu provizorního řešení se obvykle používá
princip agregace kritérií nebo princip minimalizace vzdálenosti od ideálního bodu. V rozhodovací
fázi rozhodovatel posoudí předložené provizorní řešení a jestliže je dosud nepokládá za vyhovující,
poskytne řešiteli informace o svých preferencích. Na jejich podkladě pak může řešitel stanovit nové
provizorní řešení, které bude rozhodovateli více vyhovovat. Interaktivní metody můžeme členit
následovně:
• Metody založené na informacích o mírách substituce. Míra substituce mezi i-tým a j-tým
kritériem udává, jaké zhoršení i-tého kritéria kompenzuje zlepšení j-tého kritéria o jednu
jednotku. Tyto metody jsou vhodné jen pro úlohy, v nichž se rozhodovací proměnné mění spojitě.
• Metody založené na informacích o úrovních kritérií. Rozhodovatel posuzuje úrovně jednotlivých
kritérií dosažené v provizorním řešení a zadává pro další krok nové mezní hodnoty kritérií. Tyto
metody lze použít i pro celočíselné úlohy.
• Postupy založené na výběru z množiny generovaných provizorních řešení. Řešitel předloží
rozhodovateli několik provizorních řešení, z nichž rozhodovatel vybere nejlepší variantu. Z této
informace pak řešitel vychází při generování dalších přípustných řešení.
Nejsou-li žádné doplňující informace o preferencích rozhodovatele k dispozici, jde o úlohu
nalezení množiny všech nedominovaných variant, což je úloha dosti náročná (tuto množinu
můžeme zkoumat např. metodami parametrického programování). Rozhodovatel nakonec ale
stejně musí vybrat jednu variantu, což je komplikováno tím, že množina všech nedominovaných
variant je obvykle dost rozsáhlá a nebo dokonce nekonečná. Navíc také může mít složitou
strukturu. Například i když všechny funkce v úloze (8.62) jsou lineární, tak množina všech
nedominovaných řešení může být nekonvexní (to ilustruje obr. 8.2, kde množina
nedominovaných řešení je tvořena lomenou čarou BCD).
29. Napište definici hry v normálním tvaru. Jaké znáte typy her? Uveďte příklady aplikací.
Teorie her se zabývá modelováním konfliktních rozhodovacích situací. Tyto situace můžeme členit
takto:
• antagonistické hry (co jedni hráči ztrácejí, ostatní získávají) a neantagonistické hry (mohou
existovat rozhodnutí výhodná pro všechny účastníky a jsou případně možné i kooperace mezi
hráči)
• hry s přenosnou výhrou (je možné přerozdělení výhry po ukončení hry) a hry s nepřenosnou
výhrou
• hry s úplnou informací (hráči mají před každým tahem přesnou informaci o dosavadním průběhu
hry) a hry s neúplnou informací
• konečné hry (všichni hráči mají konečně mnoho strategií) a nekonečné hry
• hry s inteligentními protihráči a hry s neinteligentními protihráči (neinteligentní protihráč
reprezentuje náhodný proces)

Příklady aplikací teorie her
• Soutěž firem o zakázky na n trzích. Předpokládá se, že získané zakázky se dělí v poměru
vynaložených prostředků na propagaci.
• Optimální úrovně výroby při oligopolu. Oligopolem se rozumí trh, na kterém se n výrobců
snaží prodat jeden druh výrobků případně výrobky vzájemně zastupitelné.
• Výběr způsobu kontroly jakosti výrobků. Protihráčem je náhodný proces, způsobující výskyt
zmetků.

30. Napište definici maticové hry. Jak ji můžeme řešit? Ilustrujte na příkladě.