Lekce - Realisticky cz

4.2.17 Cyklometrické funkce
Předpoklady: 4216
Cyklometrické funkce: funkce inverzní k funkcím goniometrickým ⇒ z minulé hodiny
známe první cyklometrickou funkci y = arcsin x (inverzní k funkci y = sin x ).
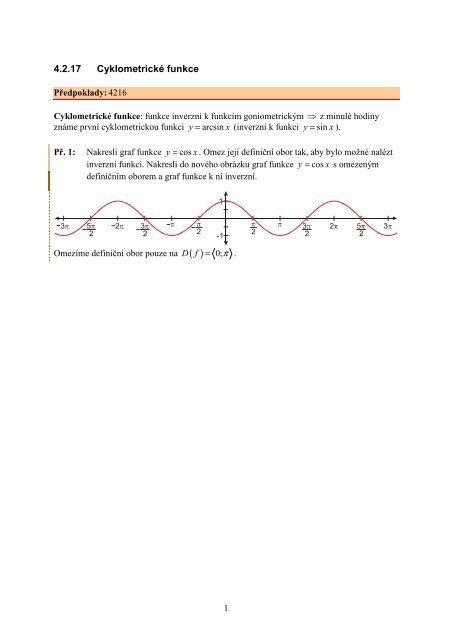
Př. 1: Nakresli graf funkce y = cos x . Omez její definiční obor tak, aby bylo možné nalézt
inverzní funkci. Nakresli do nového obrázku graf funkce y = cos x s omezeným
definičním oborem a graf funkce k ní inverzní.
1
Omezíme definiční obor pouze na D ( f ) 0;
-1
= π .
1

1
-1
1
-1 0
1
-1
Funkce inverzní k funkci
y = cos x se nazývá y = arccos x (arkus kosinus).
Př. 2: Srovnej v tabulce vlastnosti funkcí y = cos x (s omezeným definičním oborem) a
y = arccos x .
y = cos x
y = arccos x
D ( f ) = 0; π
D ( f ) = − 1;1
H ( f ) = − 1;1
( ) = 0;
H f π
funkce je klesající
funkce je klesající
2

⎛ 2 ⎞
Př. 3: Urči: a) arccos1 b) arccos
⎜
−
2 ⎟
c) arccos0
⎝ ⎠
d)
3
arccos e) arccos ( − 1)
f) arccos ( 2)
2
− .
a) arccos1 = 0
(protože cos 0 = 1)
⎛ 2 ⎞ 3
b) arccos
⎜
− =
2 ⎟ 4 π
3 2
(protože cos π = − )
⎝ ⎠
4 2
π
π
c) arccos0 = (protože cos = 0 )
2
2
⎛ 3 ⎞ π
π 3
d) arccos
⎜
=
2 ⎟
(protože cos = )
⎝ ⎠ 6
6 2
arccos − 1 = π
(protože cosπ = − 1)
e) ( )
f) arccos ( 2)
neexistuje
− = (protože funkce y = cos x nemá nikdy hodnotu -2)
Př. 4:
Urči pomocí kalkulačky ve stupních s přesností na minuty přibližné hodnoty:
2
⎛ π ⎞
a) arccos 0, 2 b) arccos ( − 0,7)
c) arccos d) arccos ⎜ − ⎟
3
⎝ 6 ⎠ .
a) arccos0,2 78°
28′
c)
arccos − 0,7 ≐ 134°
26′
≐ b) ( )
⎛ 2 ⎞
⎛ π ⎞
arccos ⎜ ⎟ ≐ 48°
11′
d) arccos ⎜ − ⎟ 121°
34′
⎝ 3 ⎠ ⎝ 6 ⎠ ≐
1
⎛ π ⎞
Př. 5: Urči v obloukové míře: a) y = arccos b) arccos ⎜ − ⎟ . Hledané hodnoty
3
⎝ 4 ⎠
nejdříve odhadni, poté je urči s pomocí kalkulačky s přesností na setiny.
π
Funkce arccos je klesající, platí arccos0 = ≐ 1,57 ⇒ hledaná hodnota bude větší než
2
π π 1
≐ 1,05 a menší než ≐ 1,57 . Kalkulačka: arccos 1,23rad
3
2
3 ≐ .
π
2 3
− ≐ −0,79
. Funkce arccos je klesající, platí arccos− = 2,36
4
2 4 π ≐ ⇒ hledaná hodnota
bude větší než 3 2,36
4 π ≐ a menší než 5 ⎛ π ⎞
π ≐ 2,62 . Kalkulačka: arccos ⎜ − ⎟ 2, 47 rad
6 ⎝ 4 ⎠ ≐ .
Př. 6: Najdi všechna x, pro která platí cos x = − 0,8.
-0,8 není tabulková hodnota funkce y = cos x ⇒ nemůžeme přesně určit hodnotu úhlu x.
arccos − 0,8 ≐ 143°
8′ .
Přibližná hodnota stanovená pomocí kalkulačky je rovna ( )
3

Přesně musíme zapisovat požadovaný úhel, pro který platí cos x = − 0,8, pomocí funkce
arccos jako arccos ( − 0,8)
.
Platí tedy x
1
= arccos ( − 0,8)
. Z jednotkové kružnice zjistíme, zda existují další taková čísla:
1
T
x 1
-1
x 2
S
R 1
T
-1
Z obrázku je vidět, že v intervalu 0;2π existují dvě hodnoty x, pro které platí cos x = − 0,8:
x = ( − ) a x π ( )
1
arccos 0,8
2
= 2 − arccos − 0,8 .
Funkce y = cos x je periodická s nejmenší periodou 2π ⇒ cos x = − 0,8 platí pro všechna
čísla ∪ = { arccos ( − 0,8) + k ⋅2 π;2π − arccos ( − 0,8)
+ k ⋅ 2π
} .
k∈Z
Podobně budeme postupovat i u dalších goniometrických funkcí:
4

Př. 7: Nakresli graf funkce y = tg x . Omez její definiční obor tak, aby bylo možné nalézt
inverzní funkci. Nakresli do nového obrázku graf funkce y = tg x s omezeným
definičním oborem a graf funkce k ní inverzní.
4
3
2
1
-1
-2
-3
-4
⎛ π π ⎞
= ⎜ − ⎟
⎝ 2 2 ⎠ .
Omezíme definiční obor pouze na ( ) ;
D f
5

4
3
2
1
-1
-2
-3
-4
6

4
3
2
1
-4
-3
-2
-1 1 2 3 4
-1
-2
-3
-4
Funkce inverzní k funkci
y = tg x se nazývá y = arctg x (arkus tangens).
Př. 8: Srovnej v tabulce vlastnosti funkcí y = tg x (s omezeným definičním oborem) a
y = arctg x .
y = tg x
y = arctg x
π π ⎞
⎟
2 2 ⎠
( ) = − ;
D f
⎛
⎜
⎝
D ( f )
= R
⎛ π π ⎞
⎜ ⎟
⎝ 2 2 ⎠
funkce je rostoucí
funkce je lichá
H ( f ) = R
H ( f ) = − ;
funkce je rostoucí
funkce je lichá
7

Př. 9: Urči: a) arctg1 b) arctg− 3
c) arctg 0
d) arctg− 1
e)
3
arctg 3
.
π
π
a) arctg1 = (protože tg = 1 )
4
4
π
⎛ 1
b) arctg ( − 3)
= − (protože tg 3
3
3 π ⎞
⎜ − ⎟ = − )
⎝ ⎠
c) arctg 0 = 0
(protože tg 0 = 0 )
d) arctg ( 1)
e)
π
⎛ π ⎞
− = − (protože tg⎜
− ⎟ = −1
4
⎝ 4 ⎠
⎛ 3 ⎞ π
arctg
⎜
=
3 ⎟
⎝ ⎠ 6
(protože
⎛ π ⎞ 3
tg⎜
⎟ = )
⎝ 6 ⎠ 3
Př. 10: Urči pomocí kalkulačky přibližně ve stupňové míře:
a) arctg− 10 b) arctg 0,4 c) arctg 2π d) arctg 520 .
arctg −10 ≐ − 84°
17′
b) arctg 0,4 ≐ 21°
48′
a) ( )
c) arctg 2π ≐ 80°
57′
d) arctg 520 ≐ 89°
53′
Př. 11: Najdi všechna x, pro která platí tg x = 2 .
2 nepatří mezi tabulkové hodnoty funkce y = tg x ⇒ nemůžeme přesně určit hodnotu úhlu x.
Přibližná hodnota stanovená pomocí kalkulačky je rovna arctg 2 ≐ 63°
26′ .
Přesně x
1
= arctg 2 .
⎛ π π ⎞
Funkce y = tg x je v rámci své jedné periody (například v intervalu ⎜ − ; ⎟ ) prostá (viz.
⎝ 2 2 ⎠
graf nahoře) ⇒ nemusíme hledat další hodnoty x, protože všechny další už se vyskytují
v jiných periodách.
tg x = 2 platí pro všechna čísla ∪ = { arctg 2 + k ⋅π}
.
k∈Z
)
Poslední goniometrickou funkcí je funkce
y = cotg x .
8

Př. 12: Nakresli graf funkce y = cotg x . Omez její definiční obor tak, aby bylo možné nalézt
inverzní funkci. Nakresli do nového obrázku graf funkce y = cotg x s omezeným
definičním oborem a graf funkce k ní inverzní.
4
3
2
1
-1
-2
-3
-4
Omezíme definiční obor pouze na D ( f ) ( 0; π )
= .
9

4
3
2
1
-1
-2
-3
-4
10

4
3
2
1
-4
-3
-2
-1 1 2 3 4
-1
-2
-3
-4
Funkce inverzní k funkci
y = cotg x se nazývá y = arccotg x (arkus kotangens).
Př. 13: Srovnej v tabulce vlastnosti funkcí
y = arccotg x .
y = cotg x (s omezeným definičním oborem) a
y = cotg x
y = arccotg x
( ) = ( 0; π )
D ( f ) = R
H ( f ) = R
H ( f ) = ( 0; π )
D f
funkce je klesající
funkce je klesající
Př. 14: Urči: a) arcotg− 1 b)
⎛
arccotg
⎜
−
⎝
3 ⎞
3 ⎟
⎠
c) arccotg 0 d) arccotg 3 .
a) arccotg ( 1)
− = 3
4 π (protože 3
cotg 1
4 π = − )
11

⎛ 3 ⎞ 2
b) arccotg
⎜
− =
3 ⎟ 3 π
⎛ 2 ⎞ 3
(protože cotg ⎜ π ⎟ = − )
⎝ ⎠
⎝ 3 ⎠ 3
π
π
c) arccotg ( 0)
= (protože cotg = 0 )
2
2
π
π
d) arccotg 3 = (protože cotg = 3 )
6
6
Př. 15: Urči pomocí kalkulačky přibližně ve stupňové míře:
a) arcotg 0,1 b) arcotg 5 c) arcotg− 2 .
1
Problém: Většina kalkulaček neosahuje tlačítko funkce arccotg x ( cot − ), kalkulačky mají
1
pouze tlačítko funkce arctg x ( tan − ).
⇒ použijeme vzorec tg x ( cotg x) −1
vypočteme úhel x.
a) arccotg 0,1 84°
17′
b) arccotg5 11°
19′
= , z hodnoty cotg x určíme hodnotu tg x a z ní
−
≐ ( x x ( ) 1
cotg = 0,1⇒ tg = 0,1 = 10 , arctg10 ≐ 84°
17′ )
−
≐ ( x x ( ) 1
cotg = 5 ⇒ tg = 5 = 0,2 , arctg 0, 2 ≐ 11°
19′ )
−
c) arccotg ( − 2)
≐ 153°
26′ ( cotg x = −2 ⇒ tg x = ( − 2) 1
= − 0,5 , ( ) ≐
y = arccotg x má hodnoty pouze v intervalu ( 0;π ) ⇒ k hodnotě ( )
přičtem 180° ⇒ arccotg ( − 2)
≐ 153°
26′ )
arctg − 0,5 26°
34′ , funkce
arctg −0,5 ≐ − 26°
34′
Př. 16: Najdi všechna x, pro která platí cotg x = − 3. Výsledek urči přibližně pomocí
kalkulačky i přesně pomocí cyklometrické funkce.
Protože -3 nepatří mezi tabulkové hodnoty funkce
hodnotu úhlu x.
y = cotg x , nemůžeme přesně určit
arccotg − 3 ≐ 161°
34′ .
Přibližná hodnota stanovená pomocí kalkulačky je rovna ( )
(podrobněji u kalkulaček, které mají pouze funkci tangens:
−
cotg x 3 tg x ( 3) 1 1 ⎛ 1 ⎞
= − ⇒ = − = − , arctg ⎜ − ⎟ ≐ − 18°
26′
, funkce arccotg
3 ⎝ 3 ⎠ y = x má hodnoty
⎛ 1 ⎞
pouze v intervalu ( 0;π ) ⇒ k hodnotě arctg ⎜ − ⎟ ≐ − 18°
26′
přičteme 180° ⇒
⎝ 3 ⎠
arccotg − 3 ≐ 161°
34′ )
( )
Přesně musíme zapisovat požadovaný úhel, pro který platí cotg x = − 3 pomocí funkce arcoctg
jako arccotg ( − 3)
.
Platí tedy x
1
= arctg ( − 3)
.
Funkce y = cotg x je v rámci své jedné periody (například v intervalu ( 0;π ) ) prostá (viz. graf
nahoře) ⇒ nemusíme hledat další hodnoty x, protože všechny další už se vyskytují v jiných
periodách.
cotg x = − 3 platí pro všechna čísla ∪ = { arctg ( − 3)
+ k ⋅π}
.
k∈Z
12

Př. 17: Petáková:
strana 44/cvičení 43, 44 hodnoty arccos , arctg , arccot
Shrnutí:
13