Fourierov rad priebehov:

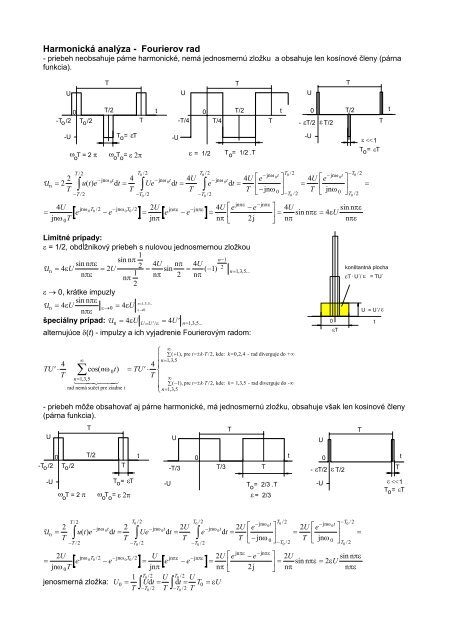
Harmonická analýza - Fourierov rad- priebeh neobsahuje párne harmonické, nemá jednosmernú zložku a obsahuje len kosínové členy (párnafunkcia).UT T TUU-T /2 o-U0T /2 oT/2T o= εTTω oT = 2 π ω oT =o ε 2πt-U0-T/4 T/4ε = 1/2z z zT / 2T0/ 2T0/ 2− jnω0t− jnω U0t− jnω0tU n ute () t Ue t eT/2T = 1/2 .T ojnπεT− jnωt− jnπεt-U0- εT/2= 2 2 d = 4 d = 4 d =4 00U e4 UtTTTT −jnωT−T/ 2−T/ 20−T/ 24U jn − jn 2 jn − jn 4 −0 0 2 0 0 2= − = − =jn T e ω T / e ω T / U U e eeπε eπεω jnπ nπ2j0Limitné prípady:ε = 1/2, obdĺžnikový priebeh s nulovou jednosmernou zložkou1sin nπn−1sin nπεnU n = 4 = 22 4Uπ 4UεUU = sin = ( −1) 2=n1n 135 , , ...πεnπnπ2 nπ2ε → 0, krátke impuzlysin nπε= 135U n = 4εUε→0 = 4εU n , , ...ε→0nπεšpeciálny prípad: U n = 4εUU= U′ / ε= 4U′ n=135 , , ...alternujúce δ(t) - impulzy a ich vyjadrenie Fourierovým radom:∞TU′ ⋅ 4 n t TU T∑ cos( ω = ′ ⋅40 )n=135 ,,TRS|T|0LNMLNMOQT / 2OQPL=NM−T/0 2∞∑ ( + 1), pre t= ± k⋅ T / 2, kde: k= 0, 2,4 - rad diverguje do + ∞n=135 , ,∞ ∑ ( −1),pre t= ± k⋅ T / 2, kde: k= 13 , , 5 - rad diverguje do -∞rad nemá sučet pre ziadne tn=135 ,,0ε T/2− jnωtejnω0T/2OQ−T/ 2Tε

Limitné prípady:ε = 1/2, obdĺžnikový priebeh s jednosmernou superpozíciou (len nepárne harmonické)1sin nπn−1sin nπεnU n = 2 =2 2Uπ 2UUεUU = sin = ( −1) 2=n1n 135 ,,...,U0=πεnπnπ2 nπ22sin nπε = 1, jednosmerný (konštantný) priebeh U n = 2Un=123 , , = 0,U0=Unπnε → 0, krátke impuzly U n = sin πε→n= n=123 , , ...2εU ε 0 2εU , U =→00 εU→0ε ε→0πεšpeciálny prípad: U n = 2εU U= U′ / ε= 2U′ n=123 , , ..., U0= U′unipolárne d(t) - impulzy a ich vyjadrenieFourierovým radom:LMNM∞∑OPQPLNMU′ ⋅ 1+2 cos( nω0t) = U′ 1+ 2 ∑( + 1) , pre t= ± k⋅ T, kde: k = 01 , ,2, 3 - rad diverguje do + ∞n=123 , ,n=123 , , QPrad nemá sučet pre ziadne tkeďže n - je nepárne aj párne v ω0 t = πrad nediverguje (nemá ale ani súčet).∞ODerivácia nasledujúcich priebehov (plné čiary) dáva predchádzajúce prípady (prerušované čiary), za predpokladuže: U = 2V/(εT) viete to využiť pri ich harmonickej analýze. Dajú sa podobne využiť prv uvedenépriebehy aj vtedy keď majú jednosmernú zložku?TTTVVVT/20T/2t 0T/2 t0t-T /2 o-VT /2 oT o= εTω oT = 2 π ω oTo= ε 2πT-T/4 T/4-Vε = 1/2T = 1/2 .T oA jeden príklad z praxe – dvojcestne usmernený priebehUu(t) = U sin( πt)TT- εT/2-Vε T/2ε