2_ Brzine prenosa toplote i mase
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
2. BRZINE PRENOSA TOPLOTE I MASE<br />
2.1 Molekulski prenos <strong>toplote</strong> i <strong>mase</strong><br />
Molekulski prenos <strong>toplote</strong><br />
Posmatrajmo sloj nepokretnog gasa ili tečnosti ili sloj čvrstog materijala čiji krajevi<br />
tj. granične površine imaju različite temperature. Kao rezultat spontane težnje ka<br />
uspostavljanju termičke ravnoteže dolazi do <strong>prenosa</strong> <strong>toplote</strong> u smeru od toplije prema<br />
hladnijoj površini.<br />
U pitanju je molekulski mehanizam <strong>prenosa</strong> <strong>toplote</strong>, koji je rezultat haotičnog<br />
termičkog kretanja molekula supstance pri čemu dolazi do prenošenja kinetičke energije u<br />
smeru u kome temperatura opada (sa bržih na sporije molekule). Izuzetak su metali, gde su<br />
glavni prenosioci <strong>toplote</strong> slobodni elektroni.<br />
Količina <strong>toplote</strong> koja u jedinici vremena prođe kroz neku površinu A naziva se fluks<br />
<strong>toplote</strong> ili toplotni fluks (W). Ako se temperatura nekom medijumu menja samo u jednom<br />
koordinatnom pravcu z, za fluks <strong>toplote</strong> Q važi relacija:<br />
∂T<br />
Q = −λA<br />
(W )<br />
(2.1)<br />
∂z<br />
poznata pod nazivom Furijeov (Fourie) zakon. A je veličina površine, normalne na<br />
pravac duž koga se temperatura menja (osa z), a λ ( W m⋅<br />
K)<br />
je koeficijent toplotne<br />
provodljivosti sredine. Parcijalni izvod ukazuje na to da u opštem slučaju pretpostavljamo<br />
nestacionaran prenos <strong>toplote</strong>, tj. da temperatura zavisi i od vremena t: T= T( z,<br />
t)<br />
. Dalje,<br />
iz (2.1) dobijamo specifični toplotni fluks ili gustinu toplotnog fluksa q:<br />
Q ∂T<br />
2<br />
q = = −λ ( W m )<br />
(2.2)<br />
A ∂z<br />
T<br />
∂T<br />
∂z<br />
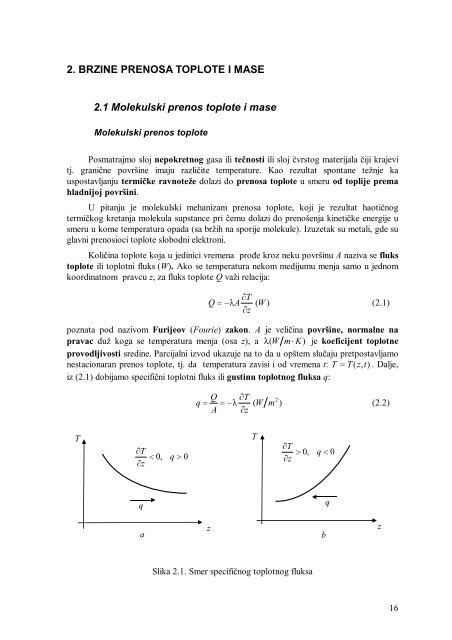
< 0 , q > 0<br />
T<br />
∂T<br />
∂z<br />
> 0 , q < 0<br />
q<br />
q<br />
a<br />
z<br />
b<br />
z<br />
Slika 2.1. Smer specifičnog toplotnog fluksa<br />
16
Znak “-” u jednačini (2.2) daje informaciju o smeru provođenja <strong>toplote</strong>, tj. o smeru<br />
toplotnog fluksa q, koji je ustvari vektorska veličina. Pozitivna brojna vrednost fluksa<br />
znači da je njegov smer jednak pozitivnom smeru z – ose (Sl. 2.1a), a ako smo dobili<br />
negativnu vrednost, znači da je njegov smer suprotan od usvojenog pozitivnog smera z -<br />
ose (Sl. 2.1b).<br />
Posmatrajmo stacionarno provođenje <strong>toplote</strong> kroz ravan zid debljine δ, čija se<br />
jedna površina (veličine A) nalazi na temperaturi T 1 , a druga na temperaturi T 2 (Sl. 2.2).<br />
T<br />
dz<br />
T<br />
1<br />
δ = z2 − z 1<br />
q<br />
T<br />
2<br />
z<br />
1<br />
z<br />
2<br />
z<br />
Slika 2.2. Temperaturni profil pri stacionarnom provođenju <strong>toplote</strong> kroz zid<br />
Pretpostavimo da se toplotna provodljivost zida ne menja sa temperaturom: λ = const. Ako<br />
unutar zida uočimo beskonačno tanak sloj debljine dz, pošto je proces stacionaran, mora<br />
ulazni fluks <strong>toplote</strong> biti jednak izlaznom :<br />
odakle sledi :<br />
q ( z)<br />
A=<br />
q(<br />
z+<br />
dz)<br />
A<br />
q=<br />
const, z≤<br />
z≤<br />
z<br />
Sada možemo da integrišemo diferencijalnu jednačinu sa datim početnim uslovom :<br />
q<br />
dT<br />
= −λ , T(z 1 ) = T 1<br />
dz<br />
1<br />
2<br />
− q<br />
z<br />
∫<br />
z<br />
1<br />
dz = λ<br />
T<br />
∫<br />
T<br />
1<br />
dT<br />
⇒<br />
q<br />
T ( z)<br />
= T1 − ( z − z1)<br />
, z1<br />
≤ z ≤ z2<br />
(2.3)<br />
λ<br />
Dakle, stacionaran temperaturni profil kroz ravan zid, pri λ = const. je linearan (slika<br />
2.2). Dalje, iz (2.3) nakon smene: z = z 2 , T(z) = T 2 , možemo da nađemo specifični toplotni<br />
fluks kroz zid:<br />
17
odnosno, apsolutna vrednost fluksa je:<br />
T<br />
q = −λ<br />
−T<br />
δ<br />
∆<br />
= −<br />
δ / λ<br />
2 1<br />
T<br />
∆T<br />
q = , Rt<br />
= δ / λ<br />
(2.4)<br />
R<br />
t<br />
Uočimo analogiju sa Omovim zakonom, pri čemu:<br />
• R t , se naziva termički otpor,<br />
• razlika ∆T = T 2 – T 1 odgovara potencijalnoj razlici,<br />
• fluks q odgovara jačini struje.<br />
PRIMER 2.1. Pokazati da je termički otpor jedinice dužine cilindrične cevi unutrašnjeg<br />
prečnika d 1 i spoljašnjeg prečnika d 2 pri λ = const. :<br />
R<br />
t<br />
d2<br />
ln<br />
d1<br />
=<br />
2πλ<br />
d2<br />
− d1<br />
=<br />
2πd<br />
λ<br />
s<br />
gde je d<br />
s<br />
srednji logaritamski prečnik, definisan kao:<br />
d − d<br />
d<br />
ln d<br />
2 1<br />
d s<br />
= .<br />
2<br />
Ukupni fluks <strong>toplote</strong> kroz bilo koji od koaksijalnih cilindara unutar zida cevi, dužine<br />
L i poluprečnika r, mora imati jednaku vrednost da bi se održala stacionarnost:<br />
dT dT<br />
d1 d2<br />
Q = −λ A = −λ 2πrL<br />
= const,<br />
≤ r ≤ (W)<br />
dr dr<br />
2 2<br />
Fluks po jedinici cevi q L biće :<br />
1<br />
q L<br />
dT d1 d2<br />
= −2πrλ<br />
= const,<br />
≤ r ≤ (W/m)<br />
dr 2 2<br />
Dobićemo ga integracijom poslednje jednačine u odgovarajućim granicama:<br />
q<br />
d<br />
2<br />
T<br />
2<br />
2<br />
dr<br />
d2<br />
∫ = −2πλ<br />
dT ⇒qL<br />
= − πλ⋅∆T<br />
r<br />
∫ ln 2<br />
d<br />
L<br />
d1<br />
2<br />
T1<br />
2πλ∆T<br />
∆T<br />
q L<br />
= − = − ⇒<br />
d2 d2<br />
ln ln /(2πλ)<br />
d d<br />
1<br />
1<br />
1<br />
d2<br />
ln<br />
d1<br />
Rt<br />
= =<br />
2πλ<br />
d2<br />
− d1<br />
d2<br />
− d<br />
2πλ<br />
d2<br />
ln<br />
d<br />
1<br />
1<br />
d2<br />
− d<br />
=<br />
2πλd<br />
1<br />
s<br />
18
Molekulski prenos <strong>mase</strong><br />
U nepokretnim medijumima, analogno prenosu <strong>toplote</strong>, difuzija komponenata je<br />
rezultat termičkog kretanja molekula i naziva se molekulska difuzija. Matematičko<br />
opisivanje molekulske difuzije je znatno složenije od opisivanja provođenja <strong>toplote</strong> jer je<br />
reč o smešama više komponenata (bar dve) čiji difuzioni fluksevi utiču jedni na druge.<br />
Uzmimo na primer najjednostavniji slučaj stacionarne difuzije u binarnoj gasnoj<br />
smeši komponenata A i B pretpostavljajući da su granice sistema propusne za obe<br />
komponente. Ako postoji promena koncentracije komponente A u pravcu z, mora da<br />
postoji i promena koncentracije komponente B, jer pri postojećem pritisku ukupan broj<br />
molekula po jedinici zapremine mora u celom sistemu biti konstantan. Tako, pošto je:<br />
važi:<br />
C A + C B = C tot. = const (mol/m 2 )<br />
dC<br />
dz<br />
A<br />
dC<br />
B<br />
= −<br />
(2.5)<br />
dz<br />
pa difunduju obe komponente i to u suprotnim smerovima. Gustina difuzionog fluksa<br />
komponente A u pravcu ose z u posmatranom slučaju data je Fikovim (Fick) zakonom<br />
dC<br />
A ⎛ mol ⎞<br />
N<br />
A<br />
= −DA<br />
⎜<br />
2<br />
⎟<br />
(2.6)<br />
dz ⎝ s ⋅ m ⎠<br />
Koeficijent D A (m 2 /s) se naziva molekulski koeficijent difuzije i u opštem slučaju zavisi<br />
od koncentracije, pritiska i temperature. Kao i za koeficijent toplotne provodljivosti, za<br />
izračunavanje difuzionog koeficijenta postoje u literaturi teorijske, poluempirijske i<br />
empirijske jednačine (Perry, 1997; Reid i sar., 1987). Iz Fikovog zakona, uz uslov<br />
D A<br />
= const. , izvodimo linearne koncentracijske profile komponenata A i B, a uzimajući<br />
u obzir uslov (2.5) i vezu između flukseva :<br />
N = −N<br />
, D = D<br />
(2.7)<br />
A<br />
B<br />
Opisanu difuziju u binarnom sistemu zovemo ekvimolarna suprotnostrujna difuzija. U<br />
praksi, ovaj slučaj imamo (približno) kod destilacije binarne smeše, pri kojoj lakše isparljiva<br />
komponenta difunduje iz tečnosti u paru, a teže isparljiva komponenta u suprotnom smeru.<br />
Analogno jednačini (2.4) za difuzioni fluks N A , opisan Fikovim zakonom (2.6), važi<br />
“električna“ analogija:<br />
D<br />
A<br />
B<br />
∆C<br />
A<br />
N<br />
A<br />
= , RD<br />
= δ / DA<br />
(2.8)<br />
R<br />
R D - difuzioni otpor<br />
δ - debljina sloja kroz koji komponenta difunduje<br />
19
Drugi slučaj stacionarne difuzije u binarnom sistemu je kada A difunduje kroz<br />
„nepokretnu“ komponentu B. To će biti slučaj ako je granica sistema propusna samo za<br />
komponentu A. Primer je apsorpcija komponente A u tečnosti. Zbog nestajanja<br />
komponente A u blizini granične površine gas - tečnost došlo bi do pada pritiska u toj<br />
oblasti. Da bi se pritisak održao konstantnim, povećava se fluks komponente A u odnosu na<br />
onaj koji daje Fikov zakon (2.6), dok je fluks nerastvorne ili inertne komponete B jednak<br />
nuli i može se izvesti:<br />
N<br />
A<br />
C<br />
A<br />
⎤ dC<br />
A<br />
⎢<br />
⎡ = − 1 + ⎥ DA<br />
(2.9)<br />
⎣ C<br />
B ⎦ dz<br />
Vidimo da je važnost Fikovog zakona (2.6) ograničena. Tako, on važi strogo ili<br />
približno u sledećim slučajevima<br />
• ekvimolarna binarna difuzija<br />
• difuzija u razblaženim multikomponentnim sistemima tj. smešama u kojima je<br />
inertna komponenta ili rastvarač u velikom višku, u odnosu na komponentu A i<br />
druge prisutne rastvorke. Na primer u slučaju difuzije A kroz nepokretan sloj<br />
komponente B, B je inert i ako je C B >> C A relacija (2.9) postaje bliska jednačini<br />
(2.6)<br />
• multikomponentna difuzija pri jednakim difuzionim koeficijentima svih<br />
komponenta, jer tada nema međusobnog uticaja flukseva<br />
Ako je neizotermičnost (neuniformnost temperature) jako izražena, neophodno je<br />
pri modelovanju difuzije uzeti u obzir i fenomen termodifuzije - difuzija koja nije<br />
uslovljena neuniformnošću koncentracije, tj. postojanjem koncentracijskog gradijenta već<br />
neuniformnošću temperature.Tada difuzionom fluksu treba dodati termodifuzioni fluks<br />
koji je proporcionalan gradijentu temperature, ∂ T∂z<br />
(Valent, 2001).<br />
Analogija između fenomena <strong>prenosa</strong><br />
Uočljiva je analogija izraza za gustine stacionarnih flukseva <strong>toplote</strong> (Furijeov zakon),<br />
komponente (Fikov zakon) i količine kretanja pri strujanju Njutnovskog fluida (Njutnov<br />
zakon):<br />
N<br />
A<br />
dT<br />
2<br />
q = −λ<br />
( W m )<br />
(2.9a)<br />
dz<br />
dCA<br />
2<br />
= −DA<br />
( mol s ⋅ m )<br />
(2.9b)<br />
dz<br />
dw<br />
2<br />
τ = −µ ( N m = Pa)<br />
(2.9c)<br />
dz<br />
τ - tangencijalni napon (fluks količine kretanja), Pa ; µ - dinamički viskozitet,<br />
Pa ⋅ s ; w - brzina sloja, koji se kreće u pravcu normalnom na z osu, m s<br />
20
Formulacije flukseva q i τ, preko koncentracija veličina koje se prenose su:<br />
λ<br />
q = −<br />
ρc<br />
p<br />
koncentrac<br />
<strong>toplote</strong> ija<br />
678<br />
d ( ρc<br />
T)<br />
dz<br />
p<br />
d(<br />
ρc<br />
pT<br />
)<br />
= −a<br />
dz<br />
(2.10)<br />
ρ - gustina,<br />
3<br />
kg m ; c p - specifična topota, J kgK ; a - termička difuzivnost, m 2 /s<br />
koncentr.<br />
kol. kretanja<br />
}<br />
µ d ( ρw)<br />
d(<br />
ρw)<br />
τ = − = −ν<br />
(2.11)<br />
ρ dz dz<br />
ν = µ ρ − kinematski viskozitet, m 2 /s .<br />
Tabela 2.1. Fluksevi preko koncentracija veličina koje se prenose<br />
Gustina fluksa<br />
veličine<br />
koja se prenosi<br />
Koncentracija<br />
veličine koja se<br />
prenosi (potencijal)<br />
Koeficijent<br />
<strong>prenosa</strong><br />
Prenos <strong>toplote</strong> q (W/m 2 ) ρc p T (J/m 2 ) a (m 2 /s)<br />
Prenos <strong>mase</strong> N A (mol/m 2 s) C A (mol/m 2 ) D A (m 2 /s)<br />
Prenos kol. kretanja τ (N/m 2 ) ρW (kg/m 2 s) ν (m 2 /s)<br />
Za modelni sistem: binarna gasna smeša molekula A i B iste veličine i <strong>mase</strong>, za koju važi<br />
kinetička teorija gasova, za sva tri transportna koeficijenta se izvodi:<br />
1<br />
D A<br />
= a = ν = w<br />
3<br />
⋅ l<br />
(2.12)<br />
w −<br />
srednja brzina molekula; l − srednja dužina slobodnog puta molekula<br />
2.2 Efektivni koeficijenti <strong>prenosa</strong> <strong>toplote</strong> i <strong>mase</strong><br />
Efektivni koeficijenti <strong>prenosa</strong> <strong>toplote</strong> i komponente se definišu pri modelovanju:<br />
• difuzije <strong>toplote</strong> i komponente kroz poroznu sredinu,<br />
• <strong>prenosa</strong> <strong>toplote</strong> i komponente kroz fluid koji struji turbulentno,<br />
sa ciljem da se navedeni fenomeni opišu jednostavnim formulama, istog oblika kao Furijeov<br />
i Fikov zakon .<br />
21
Molekulska difuzija i provođenje <strong>toplote</strong> kroz porozni medijum<br />
Pri modelovanju difuzije molekula gasa ili tečnosti kroz čvrst, porozan medijum<br />
(primer je difuzija vode kroz materijal koji se suši), dvofazni sistem fluid - čvrsto<br />
zamenjuje se kvazi - homogenim medijumom - kao da molekuli difunduju kroz celu<br />
površinu A preseka bloka poroznog čvrstog materijala, a ne samo kroz površinu A′ koju<br />
čine površine preseka pora (Sl. 2.3). Takav model se naziva kvazihomogen matematički<br />
model.<br />
A′<br />
− ukupna površina poprečnih<br />
preseka svih pora<br />
A- ukupna površina poprečnog<br />
reseka poroznog bloka<br />
Slika 2.3. Skica uz opis kvazihomogenog medijuma<br />
Tako se fluks komponente u poroznom sistemu, kroz površinu normalnu na pravac<br />
difuzije (Sl. 2.3), definiše kao:<br />
eff dCA<br />
⎛ mol ⎞<br />
N<br />
A<br />
A = −DA<br />
A ⎜ ⎟<br />
(2.14a)<br />
dz ⎝ s ⎠<br />
A - površina preseka poroznog bloka, normalna na pravac difuzije<br />
Slično, umesto da se pri konduktivnom prenosu <strong>toplote</strong> kroz porozni medijum (Sl.<br />
2.3) fluks <strong>toplote</strong> računa kao zbir flukseva kroz pore i kroz čvrst medijum, on se računa<br />
kao da je u pitanju homogena sredina, pomoću Furijeovog izraza:<br />
eff dT<br />
Q = q ⋅ A = −λ A (W )<br />
(2.14b)<br />
dz<br />
Dakle, formule (2.14a,b) imaju isti oblik kao one za molekulski prenos topolote i <strong>mase</strong> kroz<br />
homogen medijum, s tim što u njima umesto pravih koeficijenata molekulskog <strong>prenosa</strong><br />
eff eff<br />
λ i D<br />
A<br />
, figurišu efektivni koeficijenti λ i D<br />
A<br />
. Tako se efektivni koeficijenti mogu<br />
definisati na sledeći način:<br />
eff<br />
• Efektivni koeficijent molekulske difuzije DA<br />
komponente A kroz porozni medijum<br />
je parametar, koji kad se zameni u “kvazi - homogeni” Fikov izraz za fluks<br />
komponente (2.14a), daje pravu veličinu fluksa.<br />
• Efektivni koeficijent provođenja <strong>toplote</strong><br />
eff<br />
λ se definiše analogno.<br />
22
Veza između efektivnih i molekulskih koeficijenata <strong>prenosa</strong> se može teorijski izvesti<br />
samo za vrlo jednostavne, idealizovane porozne strukture, pa se efektivni koeficijenti ne<br />
izračunavaju iz pravih, nego određuju eksperimentalno. Jasno je da efektivni koeficijent<br />
difuzije neke komponente kroz porozni medijum mora da ima manju vrednost od<br />
molekulskog koeficijenta difuzije :<br />
D < D<br />
eff<br />
A<br />
A<br />
Prenos <strong>toplote</strong> i komponente kroz fluid koji struji turbulentno<br />
Posmatrajmo prenos <strong>toplote</strong> u suprotnostrujnom izmenjivaču <strong>toplote</strong> čiji smo model<br />
diskutovali u Primeru 1.1. Jednostavan matematički model (1.4) nije obuhvatio prenos<br />
<strong>toplote</strong> kroz fluide u pravcu ose izmenjivača, tj. podužno, koji svakako postoji zbog<br />
promena temperatura oba fluida duž izmenjivača. Pretpostavimo da fluid u cevi struji<br />
turbulentno. Kako opisati podužni fluks <strong>toplote</strong> kroz njega? Pošto se prenos <strong>toplote</strong> vrši ne<br />
samo molekulski nego i kao rezultat haotičnog kretanja vrtloga (vrtložni prenos <strong>toplote</strong>),<br />
nije primenljiv Furijeov zakon, koji važi samo za molekulski prenos. Ipak, radi<br />
pojednostavljenja modela, kombinovani molekulski i vrtložni prenos <strong>toplote</strong> se opisuje na<br />
analogan način kao čista kondukcija, zahvaljujući uvođenju efektivnog koeficijenta<br />
provođenja <strong>toplote</strong>:<br />
eff dT<br />
q = −λ<br />
(2.15a)<br />
dz<br />
čija je definicija analogna onoj za efektivni koeficijent kondukcije kroz poroznu sredinu. S<br />
obzirom da vrtlozi intenzifikuju prenos <strong>toplote</strong> kroz fluid, jasno je da važi:<br />
λ eff<br />
> λ<br />
gde je λ koeficijent provođenja <strong>toplote</strong> za fluid. Analogno, specifični fluks <strong>prenosa</strong><br />
komponente kroz fluid kombinovananim mehanizmom (molekulski i vrtložni) se opisuje<br />
modifikovanim Fikovim zakonom:<br />
N<br />
A<br />
eff dCA<br />
= −DA<br />
(2.15b)<br />
dz<br />
2.3 Konvektivni prenos <strong>toplote</strong> i <strong>mase</strong>. Prelaz <strong>toplote</strong> i <strong>mase</strong>.<br />
Molekulski transport <strong>toplote</strong> i <strong>mase</strong> je rezultat haotičnog kretanja molekula u<br />
nepokretnom fluidu. Molekulski mehanizam <strong>prenosa</strong> <strong>toplote</strong> i <strong>mase</strong> je takođe važeći i pri<br />
strujanju fluida, ako je ono laminarno (slojevito). Ako se pri strujanju fluida stvaraju<br />
vrtlozi (prelazni i turbulentni režim strujanja), neophodno je pri određivanju flukseva<br />
<strong>toplote</strong> i <strong>mase</strong>, uzeti u obzir i uticaj kretanja fluida. Prenos <strong>toplote</strong> ili <strong>mase</strong>, pri strujanju<br />
fluida se naziva konvektivni prenos.<br />
23
U slučaju razvijenog turbulentnog strujanja fluida, prenos <strong>toplote</strong> i <strong>mase</strong> je znatno<br />
intenzivniji nego u nepokretnom fluidu, zbog haotičnog kretanja velikih grupa ili klastera<br />
(cluster) molekula, vidljivih i golim okom, koji se zovu vrtlozi (eddy).<br />
Prelaz <strong>toplote</strong><br />
Posmatrajmo stacionarno jednodimenziono prinudno (pod dejstvom pumpe)<br />
turbulentno strujanje fluida duž ravnog zida ili ploče vrlo velike (teorijski beskonačne)<br />
površine. Uspostavljeni brzinski profil w = w(z),<br />
• je rezultat usporavajućeg dejstva zida na struju fluida potiskivanu pumpom,<br />
odnosno rezultat <strong>prenosa</strong> količine kretanja u pravcu normale na zid (osa z).<br />
• ima horizontalnu asimptotu w = w f , ako je sloj fluida vrlo velike debljine.<br />
Sloj fluida uz zid u kome brzina fluida raste od nula (u tački z = 0, tj. uz sam zid) do<br />
vrednosti 0.99w f naziva se hidraulični granični sloj i njegovu debljinu ćemo označiti sa<br />
δ H . Za z > δ H može se smatrati da je brzina uniformna i jednaka asimptotskoj vrednosti w f ,<br />
koja predstavlja brzinu turbulentne <strong>mase</strong> fluida.<br />
Slika 2.4 Brzinski i temperaturni profil<br />
Analogno, ako temperatura zida T z i temperatura dolazećeg fluida T f nisu jednake,<br />
kao rezultat <strong>prenosa</strong> <strong>toplote</strong> u z - pravcu formiraće se temperaturni profil sličnog oblika,<br />
sa horizontalnom asimptotom T = T f . Ako je T z > T f , u toplotnom graničnom sloju, širine<br />
δ T se temperatura menja od temperature zida T z do 1.01T f (Sl. 2.4).<br />
U laminarnom podsloju uz zid, fluid struji laminarno i<br />
• u njemu su najveće promene brzine strujanja i temperature fuida, tj. gradijenti<br />
dw dT<br />
i .<br />
dz dz<br />
• imamo molekulski mehanizam <strong>prenosa</strong> količine kretanja i <strong>toplote</strong><br />
• brzinski i temperaturni profili su približno linearni<br />
24
U međusloju (preostalom delu graničnog sloja) imamo :<br />
• prelazni režim strujanja.<br />
• gradijenti brzine i temperature postepeno opadaju praktično do nule, jer<br />
• vrtlozi intenzifikuju prenos količine kretanja i <strong>toplote</strong><br />
U masi fluida, snažno vrtloženje uslovljava uniformisanje brzina i temperatura.<br />
Debljina hidrauličnog graničnog sloja će biti utoliko veća ukoliko je veći fluks<br />
količine kretanja između zida i fluida (kočeće dejstvo zida), odnosno ukoliko je veći<br />
kinematski viskozitet ν (difuzivnost količine kretanja) - vidi jedn. (2.11). Analogno,<br />
debljina toplotnog graničnog sloja δ T (rastojanje do koga se “oseća” efekat zagrejane<br />
ploče na temperaturu fluida) raste sa toplotnom difuzivnošću a (vidi jedn. 2.10). Tako<br />
odnos δ H i δ T raste sa količnikom ν/a, koji se zove Prandltov kriterijum ili Prandtlov broj<br />
prema jednačini:<br />
δ<br />
δ<br />
H<br />
T<br />
=<br />
1/ 3<br />
Pr<br />
⎛ ν ⎞<br />
= ⎜ ⎟<br />
⎝ a ⎠<br />
1/ 3<br />
δ<br />
δ<br />
H<br />
T<br />
⎧<br />
⎪<br />
⎨<br />
⎪<br />
⎪⎩<br />
< 1 za Pr < 1<br />
= 1 za Pr = 1<br />
> 1 za Pr > 1<br />
(tecni<br />
metali)<br />
(idealan gas, vidi 2.12)<br />
(tecnosti i realni<br />
gasovi)<br />
Teorija filma<br />
Od praktičnog interesa je količina <strong>toplote</strong> koju zid u jedinici vremena preda fluidu,<br />
računato po jedinici površine:<br />
q<br />
z=<br />
0<br />
dT<br />
= − ⎛ ⎝ ⎜ ⎞<br />
λ ⎟<br />
(2.16)<br />
dz ⎠<br />
z=<br />
0<br />
Slika 2.5 Stvarni i aproksimativni temperaturni profil<br />
25
Jednačina (2.16) zahteva poznavanje temperaturnog profila T (z)<br />
, čije je dobijanje vrlo<br />
kompleksno (rešavanje sistema od dve diferencijalne jednačine: bilans količine kretanja i<br />
energetski bilans).Zato pravi profil zamenjujemo izlomljenim (Sl. 2.5), koji se sastoji od<br />
• kose duži (deo tangente povučene u tački z = 0) sa nagibom<br />
• horizontalog dela - asimptote T = T f .<br />
Tačka preloma, tj. presek tangente i asimptote, definiše debljinu fiktivnog toplotnog<br />
graničnog sloja, δ′<br />
T<br />
ili debljinu filma. Nagib kosog profila je,<br />
⎛<br />
⎜<br />
⎝<br />
dT<br />
dz<br />
⎞<br />
⎟<br />
⎠<br />
z=0<br />
T<br />
f<br />
− T<br />
δ<br />
'<br />
T<br />
z<br />
⎛ dT ⎞<br />
= ⎜ ⎟<br />
⎝ dz ⎠<br />
z=<br />
0<br />
pa dobijamo:<br />
q<br />
λ<br />
= − ( T<br />
−T<br />
)<br />
z=<br />
0 ' f z<br />
δT<br />
Ako se količnik λ/δ T ’ zameni novim koeficijentom α,<br />
λ<br />
α = (W/m 2 K) (2.17)<br />
'<br />
δ T<br />
dobijamo izraz za prelaz <strong>toplote</strong> sa zida na fluid:<br />
q<br />
( T −T<br />
)<br />
z=0 = −α<br />
f z<br />
(2.18)<br />
α - koeficijent konvekcije ili koeficijent prelaza <strong>toplote</strong>.<br />
Sličnim pristupom, za fluks količine kretanja sa zida na fluid dobijamo :<br />
dw C<br />
f 2<br />
τ<br />
z= 0<br />
= µ = ρ w<br />
f<br />
(2.19)<br />
dz 2<br />
z=<br />
0<br />
C<br />
f<br />
- bezdimenzioni parametar koji se naziva koeficijent trenja (friction<br />
coefficient).<br />
Primena teorije sličnosti<br />
Umesto simultanog rešavanja diferencijalnih jednačina <strong>prenosa</strong> količine kretanja i<br />
<strong>toplote</strong>,<br />
• definiše se skup bezdimenzionih grupa ili kriterijuma, (prevođenjem dif.<br />
jednačina u bezdimenzioni oblik), koje karakterišu posmatranu pojavu.<br />
26
• na bazi eksperimenata, definišu se kriterijalne jednačine, koje povezuju<br />
bezdimenzione kriterijume i to za :<br />
- pojedine klase sistema, koje se karakterišu istom geometrijom (da bi<br />
mogao da se ostvari uslov geometrijske sličnosti) i<br />
- isti režim strujanja fluida (zbog hidrodinamičke sličnosti).<br />
Tako za prinudnu konvekciju kriterijalna jednačina za određenu klasu sistema i režim<br />
strujanja glasi:<br />
Nu<br />
αL = =<br />
λ<br />
f (Re,Pr)<br />
i uobičajeni oblik za turbulentni režim strujanja je:<br />
m n<br />
Nu= c Re Pr , 0.5 ≤ m ≤0.8, 0.2 ≤ n ≤0.5 (2.20)<br />
Za detaljnije informacije u vezi sa kriterijalnim jednačinama upućujemo čitaoca na literaturu<br />
(Toledo, 1991, 2007; Perry i Green, 1997; Çengel, 1998)<br />
Značenja bezdimenzionih kriterijuma su<br />
• Re - mera relativnog uticaja inercijalnih sila (brojioc) i sila trenja (imenioc),<br />
• Pr - odnos intenziteta <strong>prenosa</strong> količine kretanja i <strong>prenosa</strong> <strong>toplote</strong>,<br />
odnosno odnos otpora prenosu <strong>toplote</strong> (1/a) i otpora prenosu količine<br />
kretanja (1/ν),<br />
• Nu - odnos uticaja turbulentnog (brojioc) i molekulskog (imenioc) mehanizma<br />
<strong>prenosa</strong> <strong>toplote</strong>, ili odnos otpora provođenju <strong>toplote</strong> L/λ i otpora<br />
konvenktivnom prenosu <strong>toplote</strong> 1/α.<br />
Za koeficijent trenja i njemu proporcionalan frikcioni faktor f, pri laminarnom<br />
strujanju kroz glatku cev važi:<br />
Gde je: f - frikcioni faktor.<br />
64<br />
f = 4 C<br />
f=<br />
(2.21)<br />
Re<br />
Za turbulentno strujanje i rapave cevi u literaturi (Perry i Green, 1997) postoje<br />
empirijske zavisnosti:<br />
Gde je:<br />
ε − koeficijent rapavosti (-).<br />
f = 4C<br />
f<br />
= F(Re,<br />
ε)<br />
(2.21a)<br />
PRIMER 2.2. Pokazati da je termički otpor prelaza <strong>toplote</strong> sa fluida na zid (ili obrnuto)<br />
cilindrične cevi prečnika d , računat po jedinici dužine cevi, jednak:<br />
1<br />
R t<br />
=<br />
π d α<br />
27
Fluks <strong>toplote</strong> kroz posmatranu površinu je ,<br />
Q = q ⋅ A = πdL<br />
⋅ q (q dato jednačinom 2.18)<br />
a po po jedinici dužine cevi :<br />
q<br />
L<br />
= πd<br />
q<br />
= πdα ∆T<br />
∆T<br />
∆T<br />
= =<br />
1 Rt<br />
πdα<br />
⇒ R<br />
t<br />
1<br />
=<br />
πdα<br />
PRIMER 2.3. Parovod spoljnjeg prečnika 10 cm sa temperaturom spoljne površine od<br />
110 0 C je izložen vetru brzine 8 m/s sa pravcem normalnim na osu parovoda. Temperatura<br />
vazduha je 4 0 C. Odrediti gubitke <strong>toplote</strong> u atmosferu po 1 m parovoda. Podaci: toplotna<br />
provodljivost i kinematski viskozitet vazduha na srednjoj temepraturi (57 o C) su<br />
BTU<br />
cm 2<br />
λ = 0.0164<br />
i ν = 670 . Proračun izvesti paralelno sa dve kriterijalne<br />
o<br />
ft ⋅ h ⋅ R<br />
h<br />
jednačine:<br />
Nu = 0.<br />
027Re<br />
0.805<br />
Pr<br />
1 3<br />
1 2 1 3<br />
5 8<br />
0.62Re Pr ⎡<br />
⎛ Re ⎞<br />
⎤<br />
Nu = 0.3 +<br />
⎢1<br />
+ ⎜ ⎟ ⎥<br />
1 4<br />
⎡ 2 3 ⎢ 282000 ⎥<br />
0 4 ⎣<br />
⎝ ⎠<br />
⎛ . ⎞<br />
⎤<br />
⎦<br />
⎢1<br />
+ ⎜ ⎟ ⎥<br />
⎢ Pr<br />
⎣<br />
⎝ ⎠ ⎥⎦<br />
Iz tablica za srednju temperaturu vazduha: Pr = 0.708. (Rešenje u Mathcad -u, fajl P 2.3)<br />
PRIMER 2.4. Idealno izolovan protočni grejač vode u obliku cevi sa električnim grejačem,<br />
dug je 5 m i ima unutrašnji prečnik 2 cm.<br />
a) Izračunati snagu grejača koja obezbeđuje zagrevanje 10 l/min vode od 15 0 C do 65 0 C<br />
b) Proceniti temperaturu unutrašnje površine grejača na izlazu, imajući u vidu da je gustina<br />
fluksa konstantna duž električnog grejača.<br />
Potrebni podaci: termofizičke osobine vode na srednjoj temepraturi (40 o C) su<br />
BTU<br />
λ = 0 .365 ,<br />
o<br />
ft ⋅ h ⋅ R<br />
2<br />
ft<br />
ν = 0.<br />
0255 ,<br />
h<br />
4 5<br />
cal<br />
g<br />
c p<br />
= 998. 1 i ρ = 0.992 .<br />
3<br />
kgK<br />
cm<br />
0.8 4<br />
Kriterijalna jednačina: Nu 0 023Re Pr<br />
0.<br />
= .<br />
Iz tablica (Cengel, 1998), za srednju temperaturu vode: Pr = 4.32. (Mathcad, P 2.4 )<br />
Prelaz <strong>mase</strong> (komponente)<br />
Analogno prenosu <strong>toplote</strong>, definiše se fluks prelaza komponente sa međufazne<br />
površine na fluid koji struji, ili obrnuto:<br />
N<br />
A<br />
A<br />
2<br />
( C − C ) ( mol m )<br />
= − β<br />
(2.22)<br />
A, f A,<br />
s<br />
s<br />
C A,f - koncentracija u turbulentnoj masi fluida<br />
C A , s - koncentracija na međufaznoj površini<br />
28
pri čemu je z - osa postavljena normalno na posmatranu površinu i usmerena od površine<br />
ka fluidu (vidi Sliku.2.5)<br />
Koeficijent prelaza komponente A, β A je u skladu sa teorijom filma:<br />
D<br />
β<br />
A<br />
A = (m/s) (2.23)<br />
'<br />
δ D<br />
Gde je: δ D ’ - debljina fiktivnog difuzionog graničnog sloja (filma)<br />
Za kriterijalnu jednačinu za prinudnu konvekciju ,<br />
uobičajeni oblik za turbulentno strujanje je :<br />
Sh= f (Re,Sc)<br />
(2.24)<br />
m n<br />
Sh= Re Sc , .5 ≤ m ≤0.8, 0.2 ≤ n ≤0.5<br />
c<br />
Šervudov (Sherwood) kriterijum Sh je analogan Nuseltovom:<br />
β<br />
Sh =<br />
A<br />
D<br />
Šmitov (Schmidt) kriterijum Sc je analogan Prandtlovom:<br />
A<br />
L<br />
Sc =<br />
ν<br />
D A<br />
Kriterijalne jednačine za različite praktične probleme se mogu naći u literaturi (Perry i<br />
Green, 1997; Çengel, 1998).U tabeli 2.2 dati su izrazi za fluks prelaza komponente, koji se<br />
koriste u praksi<br />
Tabela 2.2 - Konzistentni parovi pogonska sila - koeficijent prelaza komponente<br />
fluks : pogonska sila koef. prelaza<br />
2<br />
N A = - β A ∆C A ( mol m s ) ∆C A (mol/m 3 ) β A (m/s)<br />
m<br />
A<br />
2<br />
= −β ∆c<br />
( kg m s<br />
A<br />
A<br />
) c<br />
A<br />
3<br />
∆ ( kg m ) β A (m/s)<br />
N A = - β A,p ∆p A ( mol<br />
N A = - β A,x ∆x A ( mol<br />
2<br />
m s ) ∆ p A (Pa) β A,p (mol/m 2 Pa s)<br />
2<br />
m s ) ∆ x A ( - ) β A,x (mol/m 2 s)<br />
gde su:<br />
C<br />
A<br />
- molska koncentracija komponente,<br />
c<br />
A<br />
- <strong>mase</strong>na koncentracija komponente,<br />
p<br />
A<br />
mol<br />
3<br />
m<br />
3<br />
kg m ,<br />
− parcijalni pritisak komponente u gasnoj smeši, Pa<br />
29
x<br />
A<br />
− molski udeo komponente u smeši<br />
PRIMER 2.5. Naći formule za preračunavanje koeficijenata prelaza pri promeni načina<br />
izražavanja pogonske sile.<br />
3<br />
Veza između molske koncentracije ( mol m ) i molskog udela neke supstance je<br />
C<br />
A<br />
n<br />
=<br />
V<br />
A<br />
nA<br />
=<br />
n<br />
n<br />
V<br />
= x ρ<br />
A<br />
∗<br />
s<br />
xAρs<br />
=<br />
M<br />
n - ukupan broj molova u smeši,<br />
∗<br />
ρ s<br />
- molska gustina smeše, mol/m 2<br />
M s - mol. masa smeše, (kg/kmol)<br />
ρ s - gustina smeše (kg/m 2 )<br />
Ako zanemarimo promene molske gustine smeše sa sastavom,<br />
s<br />
*<br />
ρ<br />
s<br />
= const ⇒<br />
∆ C<br />
što nakon smene u prvi od flukseva u Tabeli 2.2 daje:<br />
N<br />
β<br />
−<br />
ρ ∆x<br />
A<br />
ρs<br />
∆x<br />
=<br />
M<br />
A s A<br />
A<br />
= = −β<br />
A,<br />
x<br />
M<br />
s<br />
s<br />
∆x<br />
A<br />
A<br />
odnosno, vezu između koeficijenta prelaza<br />
β<br />
β<br />
A, x<br />
i<br />
A<br />
:<br />
ρ<br />
s<br />
β<br />
A , x<br />
= β<br />
A<br />
(2.25)<br />
M<br />
s<br />
Veza između pogonskih sila<br />
∆ P<br />
A<br />
i ∆x<br />
je pri zanemarljivoj promena pritiska jednostavna:<br />
A<br />
p A = x A p<br />
p= const.<br />
⇒ ∆pA = ∆x A p<br />
što nakon smene u drugi od flukseva u Tabeli daje vezu između<br />
β iβ :<br />
A , x A,<br />
p<br />
β = p<br />
(2.26)<br />
A , x<br />
β<br />
A.<br />
p<br />
Iz (2.25) i (2.26) sledi konačno veza između<br />
β<br />
β<br />
A, p<br />
i<br />
A<br />
:<br />
ρ<br />
s<br />
β<br />
A , p<br />
= β<br />
A<br />
(2.27)<br />
p M<br />
s<br />
Ako je smeša idealan gas važi:<br />
ρs<br />
p = ρ<br />
∗ sRgT<br />
= RgT<br />
, pa imamo :<br />
M<br />
s<br />
30
β<br />
A<br />
β<br />
A , p<br />
=<br />
(2.28a)<br />
R g<br />
T<br />
gde je: R<br />
g<br />
β<br />
=β<br />
− univerzalna gasna konstanta.<br />
p<br />
= β<br />
ρ<br />
∗<br />
A, x A<br />
A s<br />
(2.28b)<br />
RgT<br />
PRIMER 2.6. Treba proceniti brzinu sušenja r u kg vode/(kg suve materije·s), kockica<br />
šargarepe vazduhom u fluidizovanom sloju, pretpostavljajući da je površina kockica<br />
prekrivena filmom vode.<br />
a) Izvesti sledeći izraz za traženu brzinu sušenja:<br />
0<br />
M<br />
w<br />
pw<br />
r = βw<br />
ρsv<br />
(1 − ϕ)<br />
sc<br />
s<br />
M p<br />
sv<br />
−1<br />
( )<br />
gde su:<br />
β w<br />
− koeficijent prelaza vlage sa površine, m s<br />
ρ sv<br />
− gustina suvog vazduha,<br />
kg<br />
3<br />
m<br />
M , − molekulske <strong>mase</strong> vode i suvog vazduha, kg kmol<br />
w M sv<br />
p − pritisak vazduha za sušenja, Pa<br />
0<br />
pw<br />
− napon pare vode na temperaturi sušenja, Pa<br />
ϕ − relativna vlažnost vazduha za sušenje<br />
sc<br />
− specifična površina kockica šargarepe,<br />
2<br />
m /kg suve materije<br />
b) Izračunati traženu brzinu sušenja sa sledećim podacima. Stranica kockice je a c<br />
= 1cm<br />
.<br />
3<br />
Gustina šargarepe je 1020 kg m a vlažnost x=<br />
5kg vode/kg suve materije. Relativna<br />
0<br />
vlažnost vazduha je 2%, pritisak je 101 kPa , a temperatura sušenja T= 80 C . Vazduh<br />
struji brzinom w= 12m s . Na datoj temperaturi: napon vodene, p 0 w<br />
= 47. 4kPa<br />
, viskozitet<br />
vazduha, µ = 0.0195cP<br />
. Kriterijalna jednačina koja važi za sušenje u fluidizovanom sloju<br />
(Toledo, 1991, 476str):<br />
Sh = 2+<br />
0.6Re<br />
0.5<br />
Sc<br />
0.33<br />
Kao karakteristična dimenzija kocke uzima se prečnik ekvivalentne sfere – one koja ima<br />
istu površinu kao kocka datih dimenzija.Za koeficijent difuzije vlage kroz vazduh uzeti<br />
−5<br />
2<br />
D w<br />
= 2.2×<br />
10 m s<br />
a)<br />
Brzina sušenja, pri pretpostavci da je površina kockice šargarepe prekrivena filmom<br />
vode, jednaka je fluksu prelaza vode sa površine u struju vazduha. Tako, krenućemo od<br />
izraza za specifični <strong>mase</strong>ni fluks prelaza vode, izabravši kao pogonsku silu razliku<br />
parcijalnih pritisaka vode uz samu površinu i u struji vazduha:<br />
31
m<br />
= M<br />
β<br />
∆p<br />
(2.28a)<br />
=<br />
M<br />
βw<br />
∆p<br />
R T<br />
⎛ kg<br />
⎜<br />
⎝ m s<br />
w w w,<br />
p w<br />
w<br />
w 2<br />
g<br />
Parcijalni pritisak vode uz samu površinu, pošto je na površini uspostavljena<br />
termodinamička ravnoteža, jednak je naponu pare vode na temperaturi sušenja, pa imamo:<br />
⎞<br />
⎟<br />
⎠<br />
m<br />
w<br />
= M<br />
w<br />
βw<br />
R T<br />
g<br />
∆p<br />
w<br />
= M<br />
w<br />
βw<br />
R T<br />
g<br />
0 p 1 0<br />
( p − p ) = M β ( p − p )<br />
w<br />
w<br />
w<br />
w<br />
R T<br />
g<br />
p<br />
w<br />
w<br />
p RgT<br />
je molska gustina vazduha i praktično je jednaka (zbog male relativne vlažnosti)<br />
molskoj gustini suvog vazduha,<br />
∗<br />
ρ sv<br />
. Relativna vlažnost vazduha je definisana kao<br />
ϕ = p p 0<br />
, pa je: w w<br />
0<br />
0<br />
∗ pw<br />
M<br />
w<br />
pw<br />
⎛ kg ⎞<br />
mw = M<br />
wβwρsv<br />
( 1 − ϕ) = βwρsv<br />
(1 − ϕ)<br />
⎜<br />
2<br />
⎟<br />
p<br />
M<br />
sv<br />
p ⎝ m s ⎠<br />
Konačno, da bi smo dobili brzinu sušenja u traženim jedinicama, treba pomnožiti izvedeni<br />
izraz specifičnom površinom kockice, s<br />
c<br />
računatom po kilogramu suve materije:<br />
0<br />
M<br />
w<br />
pw<br />
r = mw<br />
sc<br />
= βwρsv<br />
(1 − ϕ)<br />
sc<br />
s<br />
M<br />
sv<br />
p<br />
b) (Mathcad, P 2.6)<br />
−1<br />
( )<br />
Analogija trenja pri proticanju fluida, prelaza <strong>toplote</strong> i prelaza <strong>mase</strong><br />
I u slučaju konvektivnog <strong>prenosa</strong> <strong>toplote</strong> i <strong>mase</strong>, pored očigledne kvalitativne, postoji<br />
i kvantitativna veza, što se može naslutiti iz opštih formi kriterijalnih jednačina za prenos<br />
<strong>toplote</strong> i <strong>mase</strong> u slučaju prinudne konvekcije (2.24, 2.27). Eksperimenti su pokazali da<br />
bezdimenzione grupe ( tzv. j - faktor za toplotu i j - faktor za masu)<br />
Nu<br />
j H=<br />
(2.29a)<br />
1/3<br />
Re Pr<br />
Sh<br />
j<br />
D=<br />
(2.29b)<br />
1/3<br />
Re Sc<br />
imaju u oblasti turbulentnog režima strujanja, približne iste brojne vrednosti:<br />
gde su: j H - faktor za prenos <strong>toplote</strong>;<br />
j D - faktor za prenos <strong>mase</strong>.<br />
f<br />
jH = jD=<br />
(2.30)<br />
2<br />
što se prema autorima naziva analogija Čilton-Kolborn-a (Chilton-Colburn). Iz te<br />
analogije sledi veza između koeficijenata prelaza komponente i <strong>toplote</strong>:<br />
32
2 / 3<br />
α ⎛ DA<br />
⎞<br />
β A = ⎜ ⎟<br />
(2.31)<br />
ρC<br />
p ⎝ a ⎠<br />
PRIMER 2.7. Pri strujanju suvog vazduha temperature 25 0 C i pritiska 1 atm, brzinom<br />
2 m/s preko površine od 0.3 m 2 pokrivene slojem naftalina, izmerena količina isparenog<br />
naftalina u toku od 15 min je 12 g. Napon pare naftalina na 25 0 C je 11 Pa a njegova<br />
difuzivnost u vazduhu, D A,B = 0.61×10 -5 m 2 /s, gde A označava naftalin, a B vazduh, kroz<br />
koga naftalin difunduje. Proceniti koeficijent prelaza <strong>toplote</strong> za vazduh, pri istim uslovima<br />
proticanja i istoj geometriji sistema. Specifična toplota i toplotna difuzivnost vazduha na<br />
25 0 kJ<br />
−5<br />
2<br />
C su: c p<br />
= 1.01 , a = 2.18 × 10 m s . Iz izračunate vrednosti koeficijenta<br />
kgK<br />
prelaza naftalina β , izračunati β iβ (Rešenje u Mathcad-u, fajl P 2.7)<br />
A<br />
A,x A,<br />
p<br />
2.4 Prenos <strong>toplote</strong> i <strong>mase</strong> kroz višeslojni medijum.<br />
Prolaz <strong>toplote</strong><br />
Prenos <strong>toplote</strong> kroz tri sloja: fiktivni toplotni granični sloj prvog fluida, zid i fiktivni<br />
toplotni granični sloj drugog fluida nazivamo prolaženje ili prolaz <strong>toplote</strong> . Na Slici 2.6 dat<br />
je uprošćen temperaturni profil (u skladu sa teorijom filma), pri stacionarnom prolaženju<br />
<strong>toplote</strong> između dva fluida sa temperaturama T 1 i T 2 , kao i šema termičkih otpora.<br />
Slika 2.6 Temperaturni profil pri stacionarnom prolaženju <strong>toplote</strong><br />
Po analogiji sa Omovim zakonom, za flukseve <strong>toplote</strong> kroz pojedine slojeve važi:<br />
T1<br />
−Ti<br />
,1<br />
Ti<br />
,1<br />
−Ti<br />
,2<br />
Ti<br />
,2<br />
−T2<br />
q1<br />
= , q2<br />
= , q3<br />
=<br />
1/<br />
α d / λ 1/ α<br />
1<br />
2<br />
(2.32)<br />
33
Iz uslova stacionarnosti temperature zida sledi međusobna jednakost flukseva:<br />
q 1 = q 2 = q 2 (= q) (2.33)<br />
Nijedna od jedn. (2.32) ne omogućuje izračunavanje q jer sadrže nepoznate potencijale -<br />
intermedijalne temperature T i,1 T i,2 . Produžena jednakost (2.32) sadrži dve nezavisne<br />
jednačine, recimo q 1 = q 2 ; q 2 = q 3 , u kojima će, nakon smene izraza (2.32), figurisati<br />
nepoznate intermedijalne temperature. Rešavanjem tih jednačina dobijamo nepoznate<br />
temperature u funkciji od krajnjih - merljivih potencijala, T 1 i T 2 . Kada se dobijeni<br />
izrazi zamene u bilo koju od tri jednačine (2.32) dobijamo fluks prolaza <strong>toplote</strong> u funkciji<br />
od krajnjih temperatura:<br />
T1<br />
− T2<br />
2<br />
q = = K<br />
T<br />
( T1<br />
− T2<br />
) ( W m )<br />
(2.34)<br />
1 d 1<br />
+ +<br />
α λ α<br />
1<br />
q - fluks prolaza <strong>toplote</strong><br />
K T - koeficijent prolaza <strong>toplote</strong>.<br />
2<br />
Izraz (2.34) smo mogli da dobijemo neposrednom primenom “električne” analogije: u<br />
brojiocu je ukupna pogonska sila, a u imeniocu ekvivalentan ili ukupan otpor za tri<br />
termička otpora vezana na red (Sl.2.6).<br />
PRIMER 2.8. Gubici <strong>toplote</strong> iz izolovanog parovoda u atmosferu po jedinici dužine<br />
parovoda, se računaju kao:<br />
gde su:<br />
q<br />
L<br />
T − Ta<br />
= (W/m)<br />
1 δ z δi<br />
1<br />
+ + +<br />
α πd<br />
λ πd<br />
λ πd<br />
( α + α ) πd<br />
1<br />
1<br />
z<br />
z<br />
i<br />
i<br />
r<br />
T, T a - temperatura pare i temperatura atmosfere (K)<br />
d 1 , d 2 - unutrašnji i spoljašnji prečnik izolovanog parovoda (m)<br />
δ z , δ i - debljina zida cevi i debljina sloja izolacije (m)<br />
d z - srednji logaritamski prečnik zida cevi (m)<br />
d i - srednji logaritamski prečnik sloja izolacije (m)<br />
λ z , λ i - toplotne provodljivosti zida i izolacije (W/mK)<br />
α 1 - koeficijent prelaza sa pare na unutrašnji zid paravoda (W/m 2 K)<br />
α 2 - koeficijent prelaza <strong>toplote</strong> sa spoljne površine paravoda u atmosferu (W/m 2 K)<br />
α r - efektivni koeficijent prelaza <strong>toplote</strong> radijacijom (W/m 2 K)<br />
Efektivni koeficijent prelaza <strong>toplote</strong> radijacijom je onaj parametar, koji kad se pomnoži<br />
pogonskom silom za prelaz <strong>toplote</strong> (T 2 - T a ), daje pravu vrednost toplotnog fluksa zračenja.<br />
Tako je prema definiciji:<br />
Gde su:<br />
4 4<br />
εσ ⋅ ( T2 − Ta<br />
) = α<br />
r<br />
( T2<br />
− Ta<br />
T2<br />
)<br />
− temperatura spoljnje površine izolovanog parovoda<br />
2<br />
2<br />
34
σ - Stefan-Bolcmanova (Stephan- Boltzman) konstanta zračenja,<br />
−8<br />
2 4<br />
σ = 5.673×<br />
10 W ( m K )<br />
ε − emisivnost površine, 0 < ε ≤ 1.<br />
pa α r očigledno zavisi od temperatura,<br />
T<br />
− T<br />
T<br />
2<br />
,Ta<br />
,<br />
2 2<br />
( T + T )( T + T )<br />
4 4<br />
2 a<br />
α<br />
r<br />
= εσ = εσ<br />
2 a 2<br />
T2<br />
− Ta<br />
i za njegovo izračunavanje je neophodna procena nepoznate temperature T 2 .<br />
a) Izvesti datu formulu za toplotne gubitke<br />
b) Izvesti izraz za koeficijent prolaza <strong>toplote</strong>, baziran na unutrašnjoj površini cevi<br />
parovoda.<br />
a) Šema termičkih otpora :<br />
a<br />
R 1 - otpor prelazu <strong>toplote</strong> sa pare na unutrašnji zid parovoda<br />
R z , R i - otpori provođenju zida i izolacije<br />
R 2 - otpor prelazu <strong>toplote</strong> sa spoljašnjeg zida parovoda na atmosferu<br />
R r - efektivni otpor radijacije<br />
R<br />
1<br />
1<br />
=<br />
α πd<br />
1<br />
1<br />
,<br />
R<br />
z<br />
δ z<br />
=<br />
λ πd<br />
z<br />
z<br />
,<br />
R<br />
i<br />
δi<br />
=<br />
λ πd<br />
i<br />
i<br />
,<br />
R<br />
2<br />
=<br />
α<br />
2<br />
1<br />
πd<br />
2<br />
,<br />
R<br />
r<br />
=<br />
α<br />
r<br />
1<br />
πd<br />
2<br />
Ekvivalentan otpor :<br />
R=<br />
R+<br />
R+<br />
R+<br />
t<br />
1<br />
z<br />
i<br />
1<br />
R<br />
2<br />
1<br />
1<br />
+<br />
R<br />
r<br />
i formula se dobija nakon smene ekvivalentnog otpora u jedn.<br />
q<br />
L<br />
∆T<br />
=<br />
R<br />
t<br />
T −T<br />
=<br />
R<br />
t<br />
a<br />
b) Da bi smo, polazeći od jednačine,<br />
q<br />
L<br />
=<br />
1<br />
α πd<br />
δ<br />
z<br />
+<br />
λ πd<br />
T −Ta<br />
δi<br />
+<br />
λ πd<br />
1 1 z z i i<br />
( α<br />
r<br />
+ α<br />
2)<br />
+<br />
1<br />
πd<br />
2<br />
T −T<br />
=<br />
R<br />
t<br />
a<br />
izveli traženi izraz za koeficijent prolaza <strong>toplote</strong>, neophodno je fluks <strong>toplote</strong>, q<br />
L<br />
prikazati<br />
kao proizvod koeficijenta prolaza, K pogonske sile T − T ) i odgovarajuće površine<br />
T<br />
(<br />
a<br />
35
toplotne razmene- unutrašnje površine cevi jedinične dužine (S = π d1) i izjednačiti dva<br />
izraza za q<br />
L<br />
:<br />
Sledi,<br />
T −T<br />
R<br />
K<br />
T<br />
t<br />
a<br />
= K<br />
T<br />
1<br />
=<br />
R πd<br />
t<br />
1<br />
( T −T<br />
) πd<br />
a<br />
1<br />
i kada se smeni izraz za<br />
R<br />
t<br />
:<br />
K<br />
T<br />
=<br />
1<br />
α πd<br />
1<br />
1<br />
δ<br />
z<br />
+<br />
λ πd<br />
z<br />
z<br />
1<br />
δi<br />
+<br />
λ πd<br />
i<br />
i<br />
+<br />
( α<br />
r<br />
1<br />
+ α ) πd<br />
2<br />
2<br />
1<br />
⋅<br />
πd<br />
1<br />
Konačno,<br />
K<br />
T<br />
=<br />
1<br />
α<br />
δ<br />
+<br />
d<br />
1<br />
δ d<br />
+ +<br />
z 1 i 1<br />
1<br />
1<br />
λ<br />
zd<br />
z<br />
λidi<br />
( αr<br />
+ α<br />
2)<br />
d<br />
d<br />
2<br />
PRIMER 2.9. Treba izračunati potrebnu debljinu izolacije ( = 0.0346W<br />
( mK)<br />
)<br />
λ tavanice<br />
da se temperatura plafona ne bi razlikovala od sobne temperature više od 2 0 C . Tavanica<br />
je debela 0.5in, a koeficijent toplotne provodljivosti materijala od koga je napravljena je<br />
λ = 0.433W<br />
( mK)<br />
. Koeficijet prelaza <strong>toplote</strong> sa obe strane tavanice je α = 2.84W<br />
( m 2 K)<br />
.<br />
Temperatura vazduha na tavanu je<br />
49 0 C , a sobna temperatura 0 C<br />
20 .<br />
Na skici su naznačeni termički otpori. Najpre ćemo iz granične temperature plafona,<br />
sobne temperature i koeficijenta prelaza <strong>toplote</strong> izračunati fluks prelaza <strong>toplote</strong> sa plafona<br />
na sobni vazduh:<br />
2<br />
[( T + 2) −T] 5. W m<br />
q = α<br />
2 s s<br />
= 68<br />
On je tačno jednak fluksu prolaza <strong>toplote</strong> od vazduha tavana do vazduha u sobi:<br />
q =<br />
1 α + δ<br />
1<br />
t<br />
T0 −Ts = 5. 68W<br />
λ + δ λ + 1 α<br />
t<br />
i<br />
i<br />
2<br />
m<br />
2<br />
odakle dobijamo traženu debljinu izolacije:<br />
⎡T0 −T<br />
⎛<br />
s<br />
1 δt<br />
1 ⎞⎤<br />
δ<br />
i<br />
= ⎢ −<br />
⎥ ⋅λi<br />
= 15. 13cm<br />
⎣ q<br />
⎜ + +<br />
⎟<br />
⎝ α1<br />
λt<br />
α<br />
2 ⎠⎦<br />
Jasno je da debljina izolacije, tražena prema datom zahtevu, ne zavisi od toga da li će<br />
se ona staviti na tavanicu ili ispod nje (na skici je uzeto da se ona postavlja ispod tavanice).<br />
36
Iz formule za fluks prolaza <strong>toplote</strong> jasno se vidi da njegova vrednost ne zavisi od redosleda<br />
termičkih otpora jer zbir u imeniocu ne zavisi od redosleda sabiraka.<br />
T 1<br />
T 0 s<br />
+ 2 C<br />
α<br />
1<br />
0<br />
T = 49 C<br />
0<br />
= 2.84W<br />
( mK)<br />
0<br />
T s<br />
= 20 C<br />
α<br />
2<br />
= α<br />
1<br />
T<br />
0<br />
1α<br />
1<br />
δ<br />
t<br />
δ<br />
i<br />
δ<br />
t<br />
λ t δ<br />
i<br />
λi<br />
1α<br />
2<br />
T<br />
s<br />
Skica uz Primer 2.9<br />
2.5 Principi opisivanja brzine složenog procesa<br />
Složeni fenomeni <strong>prenosa</strong> se, ako je moguće, dekomponuju (raščlanjuju) na više<br />
jednostavnijih fenomena koji predstavljaju stupnjeve ili stadijume složenog procesa.<br />
Oni mogu međusobno biti povezani:<br />
• serijski (uzastopni ili konsekutivni stupnjevi)<br />
• paralelno (paralelni ili uporedni stupnjevi)<br />
• na složen način koji predstavlja kombinaciju serijskih i paralelnih veza.<br />
Tako, u Primeru 2.7, gubljenje <strong>toplote</strong> pare pri transportu kroz parovod smo raščlanili na 5<br />
elementarnih stupnjeva, kao:<br />
4.<br />
prelaz <strong>toplote</strong><br />
1. 2. 2. sa spoljašnjeg<br />
prelaz <strong>toplote</strong> provođenje provođenje zida u atmosferu<br />
sa pare na <strong>toplote</strong> <strong>toplote</strong><br />
unutrašnji kroz zid kroz izolaciju 5.<br />
zid cevi prenošenje <strong>toplote</strong><br />
sa spolašnjeg zida<br />
u atmosferu<br />
zračenjem<br />
<strong>Brzine</strong> elementarnih fizičkih stadijuma (prenos <strong>toplote</strong> ili <strong>mase</strong>) se mogu prikazati u<br />
vidu količnika pogonske sile i otpora. Ako pogonska sila linearno zavisi od potencijala<br />
(temperature ili koncentracije), a otpor nije funkcija potencijala, kažemo da je<br />
37
posmatrani stadijum linearan i njegova brzina je opisana izrazom analognom Omovom<br />
zakonu (električna analogija):<br />
r<br />
V<br />
= − ∆ (2.35)<br />
R<br />
V - potencijal (temperatura ili koncentracija)<br />
R - otpor (toplotni ili difuzioni)<br />
Negativni predznak u izrazu (2.35) nosi informaciju o smeru fluksa (da li je isti kao i smer<br />
prostorne ose ili suprotan od njega) pri čemu je prostorna osa usmerena od prvog ka<br />
poslednjem stadijumu u nizu.<br />
Brzina složenog procesa, dekomponovanog na linearne stadijume dobija se<br />
pomoću električne analogije (2.35) u koju se kao ∆V zamenjuje ukupna potencijalna<br />
razlika a umesto R ukupan ili ekvivalentan otpor. Tako, ako je složeni proces niz od n<br />
linearnih uzastopnih stadijuma čije su brzine:<br />
∆Vi<br />
Vi<br />
−Vi<br />
−1 ri = − = − , i = 1,...,<br />
n<br />
R R<br />
i<br />
i<br />
(2.36)<br />
ukupna pogonska sila je:<br />
n<br />
∑<br />
∆V = ∆Vi<br />
= Vn<br />
− V0 (2.36a)<br />
i=<br />
1<br />
a ekvivalentan otpor:<br />
R=<br />
n<br />
R i<br />
i=<br />
1<br />
∑<br />
(2.36b)<br />
pa je brzina procesa:<br />
r<br />
P<br />
V<br />
= −<br />
n<br />
n<br />
∑<br />
i=<br />
1<br />
− V<br />
R<br />
i<br />
0<br />
(2.37)<br />
Metod limitirajućeg stupnja<br />
V<br />
0,V n<br />
− krajnji potencijali<br />
Posmatrajmo prolaz <strong>toplote</strong> kroz homogeni zid. <strong>Brzine</strong> tri stadijuma su date<br />
jednačinama (2.32):<br />
q<br />
1<br />
=<br />
T<br />
− T<br />
T<br />
1<br />
− T<br />
2<br />
, q2<br />
= ,<br />
R<br />
T<br />
=<br />
− T<br />
1 i, 1<br />
i, i, i,<br />
2 2<br />
q3<br />
R1<br />
2<br />
R3<br />
38
Neka je 3. stupanj znatno sporiji od ostalih, odnosno njegov otpor znatno veći od druga<br />
dva otpora, što znači:<br />
R<br />
R<br />
1<br />
3<br />
R2<br />
≈ ≈ 0<br />
R<br />
3<br />
Iz uslova jednakosti brzina prvog i trećeg stupnja:<br />
Iz drugog uslova, q 2 = q 3 imamo:<br />
q<br />
q<br />
T −T<br />
(2.32)<br />
1 i,1<br />
1<br />
1<br />
= q3<br />
⇒ = ≈0 ⇒ Ti<br />
,1<br />
≈ T1<br />
Ti<br />
,2<br />
−T2<br />
R3<br />
T<br />
−T<br />
(2.32)<br />
i,1<br />
i,2<br />
2<br />
2<br />
= q3<br />
⇒ = ≈0 ⇒ Ti<br />
,2<br />
≈ Ti<br />
,1<br />
Ti<br />
,2<br />
−T2<br />
R3<br />
Dakle, aproksimativni temperaturni profil će izgledati kao na Sl. 2.7. Pošto smo definisali<br />
intermedijalne potencijale:<br />
R<br />
R<br />
T = T = T<br />
i, 1 i,<br />
2 1<br />
sledi izračunavanje brzine <strong>prenosa</strong> <strong>toplote</strong> smenom nađenih vrednosti u izraz za brzinu<br />
nekog od stupnjeva. Međutim, pošto su, izrazi za brzine “brzih” stupnjeva q 1 i q 2<br />
0 0 preostaje izraz za spori stupanj:<br />
nedefinisani ( )<br />
T − T<br />
rP = r3<br />
=<br />
R<br />
1 2<br />
3<br />
Slika 2.7. Aproksimativni temperaturni profil troslojnog zida kada je R<br />
3<br />
>> R1, R2<br />
Zaključujemo da,<br />
• Izrazito najsporiji u nizu konsekutivnih stupnjeva definiše tj. limitira (jer<br />
je najsporiji) brzinu složenog procesa, pa se zato zove limitirajući stupanj;<br />
39
• U ostalim, relativno brzim stadijumima, približno se uspostavlja<br />
termodinamička ravnoteža, tj. pogonske sile tih stadijuma su bliske nuli;<br />
• Brzina procesa je približno jednaka brzini kojom bi se odvijao limitirajući<br />
stupanj, kad bi u svim ostalim stupnjevima bila uspostavljena termodinamič -<br />
ka ravnoteža.<br />
Metod limitirajućeg stupnja znatno pojednostavljuje problem određivanja brzine<br />
složenog procesa, naročito u slučaju kad su neki od stupnjeva nelinearni. (kao što je<br />
naprimer stadijum zračenja <strong>toplote</strong>).<br />
ZADACI<br />
2.1. Prozor sa duplim staklima razdvojenih slojem nepokretnog vazduha ima dimenzije<br />
0 . 8× 1.<br />
5m<br />
. Stakla ( λ = 0 . 451 BTU / ft ⋅ h ⋅ R ) su debela 4mm, a sloj vazduha<br />
( λ = 0 . 015 BTU / ft ⋅ h ⋅ R ) 10 mm. Ako je temperatura u sobi 20 0 C, a spoljnja<br />
temperatura -10 0 C, izračunati toplotne gubitke i temperaturu unutrašnje površine prozora.<br />
2<br />
Koeficijent prelaza <strong>toplote</strong> za unutrašnju površinu prozora je α1 = 1 . 761BTU / ft ⋅ h ⋅ R , a<br />
2<br />
za spoljašnju α12 = 7 . 044BTU / ft ⋅ h ⋅ R .<br />
2.2. Kroz zid sastavljen od 4 sloja iste debljine, toplotnih provodljivosti λ<br />
1<br />
, λ2,<br />
λ3,<br />
λ4<br />
,<br />
prenosi se toplota između leve površine, temperature T 1 i desne, temperature T 2 .<br />
T 1<br />
T 2<br />
λ 1 λ 2 λ 3 λ 4<br />
a) Skicirati temperaturni profile kroz posmatrani zid ako je treći od 4 konsekutivna stupnja<br />
limitirajući i napisati odgovarajuću formulu za fluks <strong>toplote</strong>, q<br />
b) Skicirati temp. profil i napisati izraz za q ako je : λ<br />
1<br />
≈ λ<br />
4<br />
>> λ<br />
2<br />
≈ λ<br />
3<br />
2.3. Čelična cev (λ = 45 W/mK) unutrašnjeg prečnika 0.824in i spoljašnjeg prečnika 1.05in<br />
je izolovana slojem fiberglasa (λ = 0.025 W/mK), debljine 2cm. Temperatura unutrašnjeg<br />
površine cevi 150 0 C , a spoljašnje površine izolacije 30 0 C .<br />
a) Izračunati toplotni fluks između te dve površine za 1 metar cevi, ( W m)<br />
b) Izračunati temperaturu spoljašnje površine cevi<br />
c) Proceniti traženi fluks i temperaturu koristeći metod limitirajućeg stupnja i uporediti sa<br />
prethodno dobijenim vrednostima.<br />
2.4. Projektuje se komora za zamrzavanje prehrambenih proizvoda. Zidovi i tavanica se<br />
sastoje od sledećih slojeva: sloj nerđajućeg čelika, ( λ = 14.2W<br />
( mK)<br />
) debljine 1.7mm, sloj<br />
q L<br />
40
penaste izolacije ( λ = 0.34W<br />
( mK)<br />
), debljine 10cm, sloj plute ( λ = 0.043W<br />
( mK)<br />
) i sloj<br />
drveta ( λ = 0.43W<br />
( mK)<br />
), debljine 1.27cm. Temperatura u zamrzivaču je − 40<br />
0 C , a<br />
temperatura okolnog vazduha je 32 0 C . Koeficijent prelaza <strong>toplote</strong> na strani nerđajućeg<br />
čelika je 5W ( m 2 K)<br />
, a sa strane drveta 2W<br />
( m 2 K ) . Ako je tačka rose spoljnjeg vazduha<br />
0<br />
29 C , izračunati minimalnu debljinu sloja plute da bi se sprečila kondenzacija vazduha na<br />
spoljnjoj površini komore.<br />
2.5. Radi određivanja toplotne provodljivosti, uzorak govedine oblika cilindra, dužine 5 cm<br />
i prečnika 3 .75cm<br />
, smešten je između dva cilindra od akrila ( λ = 1.5W mK ), istog<br />
prečnika i sve je to stavljeno u izolovani kontejner (skica). Slobodne površine akrilnih<br />
cilindara (na dnu donjeg i na vrhu gornjeg cilindra) se održavaju na konstantnim<br />
temperaturama, pri čemu je donja površina na višoj temperaturi. U oba akrilna cilindra su<br />
stavljena po dva termopara i to na rastojanju 0.5 i 1 cm od dodirne površine sa uzorkom.<br />
Termoparovi (počev od najnižeg) su registrovali sledeće temperature: 45 , 43, 15 i13<br />
0 C .<br />
Izračunati,<br />
a) Specifični toplotni fluks, q kroz uzorak i akrilne cilindre.<br />
b) Temperature donje i gornje površine uzorka<br />
c) Toplotnu provodljivost λ goveđeg mesa.<br />
5 cm<br />
3.75 cm<br />
Skica uz zadatak 2.5<br />
2.6. Unutrašnja cev izmenjivača <strong>toplote</strong> ima unutrašnji prečnik 2 .21cm<br />
i zid debeo<br />
1 .65mm . Koeficijent prelaza <strong>toplote</strong> sa unutrašnje strane cevi α<br />
1<br />
= 568W m<br />
2 K , a sa<br />
spoljašnje, α<br />
2<br />
= 5678W m<br />
2 K .Toplotna provodljivost cevi je λ = 55.6W mK . Izračunati,<br />
a) koeficijent prolaza <strong>toplote</strong> kroz cev, baziran na unutrašnjoj površini cevi,<br />
41
) temperaturu unutrašnje površine cevi, ako je temperatura fluida u cevi 80 0 C , a<br />
temperatura fluida oko cevi 120<br />
0 C<br />
2.7. 50 kg h koncentrata jabukovog soka ( c p<br />
= 3. 187 kJ kgK ) se hladi od 80 do 20 0 C u<br />
suprotno-strujnom izmenjivaču <strong>toplote</strong>, cev u cevi. Rashladna voda ulazi u izmenjivač na<br />
temperaturi 10 0 C , a izlazi na 17 0 C . Koeficijent prolaza <strong>toplote</strong> u izmenjivaču je<br />
2<br />
K T<br />
= 568W<br />
m K . Izračunati,<br />
a) protok rashladne vode<br />
b) potrebnu površinu toplotne razmene.<br />
2.8. Izvesti sledeći izraz za termički otpor (otpor provođenju <strong>toplote</strong>) sferne ljuske sa<br />
unutrašnjim i spoljašnjim poluprečnicima r 1 i r 2<br />
R t<br />
r2<br />
− r1<br />
=<br />
4πr<br />
r λ<br />
1<br />
2<br />
2.9. a) Izvesti izraz za brzinu difuzije F A komponente A kroz porozni zid u obliku sferne<br />
ljuske sa unutrašnjim i spoljašnjim poluprečnikom r 1 i r 2 .<br />
F<br />
4<br />
r<br />
r<br />
D<br />
C<br />
( r ) − C<br />
( r<br />
A 1 A 2<br />
A<br />
= π<br />
1 2 A,<br />
B<br />
(mol/s)<br />
r2<br />
− r1<br />
)<br />
b) Helijum je skladišten u sferni rezervoar spoljnjeg prečnika 3 m i debljine zida 5 cm od<br />
pireksa na 20 0 C. Molska koncentracija helijuma u pireksu je 0.73 mol/m 3 na unutrašnjoj<br />
površini zida a zanemarljiva na spoljnjoj površini. Difuzivnost helijuma kroz pireks na 20 0 C<br />
D A,B = 4.5×10 -15 m 2 /s. Odrediti dnevne gubitke helijuma difuzijom kroz zid rezervoara.<br />
2.10. Za laminarno strujanje kroz cevovod, izvodi se sledeći brzinski profil:<br />
( r)<br />
= 2w<br />
w<br />
sr<br />
⎛<br />
⎜ ⎛<br />
1−<br />
⎜<br />
⎝ ⎝<br />
r<br />
R<br />
⎞<br />
⎟<br />
⎠<br />
2<br />
⎞<br />
⎟<br />
⎠<br />
gde je w<br />
sr<br />
srednja brzina proticanja,a R unutrašnji poluprečnik cevovoda. Za tangencijalni<br />
napon na površini cevi važi jedn. (2.19), s tim što umesto w<br />
f<br />
treba staviti w<br />
sr<br />
. Koristeći<br />
jedn (2.19) i Njutnov zakon (2.9c), izvesti izraz (2.21) za koeficijent trenja.<br />
42