fH D FB 4 - HTL Wien 10

fH D FB 4
Fachhochschule Düsseldorf
University of Applied Sciences
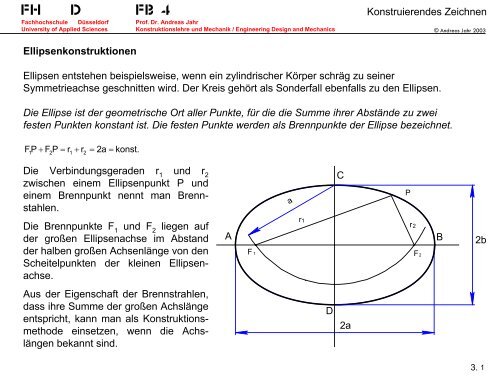
Ellipsenkonstruktionen
Konstruierendes Zeichnen
Prof. Dr. Andreas Jahr
Konstruktionslehre und Mechanik / Engineering Design and Mechanics © Andreas Jahr 2003
Ellipsen entstehen beispielsweise, wenn ein zylindrischer Körper schräg zu seiner
Symmetrieachse geschnitten wird. Der Kreis gehört als Sonderfall ebenfalls zu den Ellipsen.
Die Ellipse ist der geometrische Ort aller Punkte, für die die Summe ihrer Abstände zu zwei
festen Punkten konstant ist. Die festen Punkte werden als Brennpunkte der Ellipse bezeichnet.
F1 P + F2P
= r1
+ r2
=
2a
=
konst.
Die Verbindungsgeraden r 1 und r 2
zwischen einem Ellipsenpunkt P und
einem Brennpunkt nennt man Brennstahlen.
Die Brennpunkte F 1 und F 2 liegen auf
der großen Ellipsenachse im Abstand
der halben großen Achsenlänge von den
Scheitelpunkten der kleinen Ellipsenachse.
Aus der Eigenschaft der Brennstrahlen,
dass ihre Summe der großen Achslänge
entspricht, kann man als Konstruktionsmethode
einsetzen, wenn die Achslängen
bekannt sind.
a
r1
A B
F 1 F2
D
C
2a
P
r2
2b
3. 1

fH D FB 4
Fachhochschule Düsseldorf
University of Applied Sciences
Konstruierendes Zeichnen
Prof. Dr. Andreas Jahr
Konstruktionslehre und Mechanik / Engineering Design and Mechanics © Andreas Jahr 2003
Konstruktion einer Ellipse mit Hilfe der Scheitelkreise
Wenn der Mittelpunkt, die Scheitelkreisradien und die Ellipsenachsen bekannt sind, kann jeder
weitere Punkt der Ellipse folgendermaßen konstruiert werden:
Man bildet die Schnittpunkte einer durch den Mittelpunkt gehenden (radialen) Geraden mit den
Scheitelkreisen. In den Schnittpunkt dieser Geraden mit dem großen Scheitelkreis legt man eine
Parallele zur kleinen Ellipsenachse und in den Schnittpunkt mit dem kleinen Scheitelkreis eine
Parallele zur großen Ellipsenachse. Diese beiden Parallelen schneiden sich in einem Punkt der
Ellipse.
a
b
3. 2

fH D FB 4
Fachhochschule Düsseldorf
University of Applied Sciences
Konstruierendes Zeichnen
Prof. Dr. Andreas Jahr
Konstruktionslehre und Mechanik / Engineering Design and Mechanics © Andreas Jahr 2003
Konstruktion einer Ellipse als affine Abbildung eines Kreises
Eine (perspektivisch) affine Abbildungen einer Ebene E 1 (und ihrer Punkte) entsteht durch
Parallelprojektion ihrer Punkte auf die Abbildungsebene E 2 .
Eigenschaften einer (perspektivischen) affinen
Abbildung:
• Jeder Punkt P 1 der Eben 1 ist umkehrbar eindeutig ein
Punkt P 2 der Ebene 2 zugeordnet
• Die zugeordneten Punkte P 1 und P 2 liegen auf einem
Affinitätsstrahl. Die Affinitätsstahlen sind zueinander
parallel.
• Jeder Geraden g 1 der Ebene E 1 ist umkehrbar eindeutig
eine Gerade g 2 der Ebene E 2 zugeordnet.
• Einander zugeordnete Geraden scheiden sich auf der
Affinitätsachse x 12
Hieraus ergeben sich zwei wesentliche unveränderliche
Eigenschaften (Invarianten) der affinen Abbildung:
• Parallel Geraden in der Ebene E 1 bleiben in der Ebene
E 2 zueinander parallel.
• Das Abstandsverhältnis dreier Punkte auf einer Geraden
der Ebene E 1 bleibt in der Ebene E 2 erhalten.
E 2
g 1
g 2
P 2
P 1
E 1
Affinitätsstrahl
x 12
3. 3

fH D FB 4
Fachhochschule Düsseldorf
University of Applied Sciences
Konstruktion einer Ellipse als affine Abbildung
Konstruierendes Zeichnen
Prof. Dr. Andreas Jahr
Konstruktionslehre und Mechanik / Engineering Design and Mechanics © Andreas Jahr 2003
Gegeben sind die Mittelpunkte des Kreises M1 und der
Ellipse M2 sowie die Affinitätsachse (Rissachse x12). Um die
unverzerrten (aufeinander senkrechten) Scheitelachsen von
Kreis und Ellipse zu finden, muss der Thaleskreis konstruiert
werden. Hierzu werden die Mittelpunkte durch eine Gerade
verbunden, deren Mittelsenkrechte die Affinitätsachse im
Punkt MT schneidet. Dies ist der Mittelpunkt des gesuchten
Thaleskreises. Die Verbindungslinien der Mittelpunkte M1 und M2 mit den Schnittpunkten des Thaleskreises mit der
Affinitätsachse bilden mit dieser rechtwinklige Dreiecke.
Zeichnet man nun einen Kreis mit dem Mittelpunkt M1 , so
wird dieser durch die in seiner Ebene liegenden
Verbindungslinie in vier Quadranten geteilt. Die
Quadrantenpunkte am Kreis werden parallel zur
Verbindungslinie der Mittelpunkte mit den den Geraden des
rechtwinkligen Dreiecks in der Ebene E2 zum Schnitt
gebracht. Die so entstandenen Schnittpunkte sind die
Scheitelpunkte der Ellipse.
Die Kathetengeraden der beiden rechtwinkligen Dreiecke
sind die einzigen orthogonalen Geradenpaare der affinen
Abbildung.
x 12
E 1
M 2
M T
M 1
E 2
affine Abbildung (Ellipse)
abzubildender Kreis
Thaleskreis
3. 4

fH D FB 4
Fachhochschule Düsseldorf
University of Applied Sciences
Sobald die Kathetengeraden der
affinen Abbildung bekannt sind,
kann zu jedem Punkt P 1 der Ebene
E 1 der entsprechende Punkt P 2 der
Ebene E2 konstruiert werden.
Hierzu werden durch den Punkt der
Ebene 1 Parallelen zu den
Katheten des rechtwinkligen
Dreiecks gezogen. Durch deren
Schnittpunkte mit der
Affinitätsachse x 12 wiederum
werden Parallelen zu den Katheten
des rechtwinkligen Dreiecks in der
Abbildungsebene E2 angetragen.
Diese schneiden sich im
entsprechenden abgebildeten
Punkt P 2 .
Diese Abbildungsvorschrift gilt
somit nicht nur für die Abbildung
der Punkte auf dem Kreis, sondern
für jeden Punkt.
Konstruierendes Zeichnen
Prof. Dr. Andreas Jahr
Konstruktionslehre und Mechanik / Engineering Design and Mechanics © Andreas Jahr 2003
P 2
x 12
E 1
P 1
M 2
M T
abzubildender Kreis
M 1
E 2
affine Abbildung (Ellipse)
Thaleskreis
3. 5

fH D FB 4
Fachhochschule Düsseldorf
University of Applied Sciences
Konstruierendes Zeichnen
Prof. Dr. Andreas Jahr
Konstruktionslehre und Mechanik / Engineering Design and Mechanics © Andreas Jahr 2003
Konstruktion einer Ellipse in ein Parallelogramm
Die affine Abbildung eines Kreises ist im Allgemeinen eine Ellipse. Diese kann mit Hilfe der affinen
Abbildung des umschreibenden Quadrates konstruiert werden, wekches ein Parallelogramms bildet.
Ein Hilfskreis wird auf der schmalen Seite des Parallelogramms errichtet und durch Höhenlinie in
halbierenden Abständen (a, a/2, a/4, usw.) parallel zur Parallelogrammseite unterteilt. Von den
Schnittpunkten werden Senkrechte auf die Parallelogrammseite errichtet. Von den Fußpunkten der
Lote zieht man Parallele zur langen Parallelogrammseite, die dann wieder in wiederholt
halbierenden Abständen durch Parallele zur kurzen Parallelogrammseite geteilt werden. Die
entsprechenden Schnittpunkte sind auch Punkte der gesuchten Ellipse.
umschreibendes Parallelogramm
A
D
C
b b/2 b/4
B
Hilfskreis
a a/2
a/4
3. 6

fH D FB 4
Fachhochschule Düsseldorf
University of Applied Sciences
Konstruierendes Zeichnen
Prof. Dr. Andreas Jahr
Konstruktionslehre und Mechanik / Engineering Design and Mechanics © Andreas Jahr 2003
Konstruktion einer Ellipse aus konjungierten Durchmessern (Rytzsche Achsenkonstruktion)
Gegeben sind die Mittelpunkte der Ellipse M sowie ein Paar Radien auf konjungierten Achsen
(Achsen, die im unverzerrten Bild, dem Kreis, senkrecht aufeinander stehen) mit den
Ellipsenpunkten Q und P. Q wird nach P um 90° gedreht und man erhält R. Um der Mitte zwischen
R und P schlägt man einen Kreisbogen durch M. Die Verlängerung der Geraden RP ergibt mit dem
Kreisbogen die Punkte U und V. Die Länge PU ist der große Ellipsenradius. Den zugehörigen
Scheitelpunkt A findet man auf der Verlängerung von VM. Den kleinen Radius PV trägt man auf der
Verlängerung von UM an. Damit Hat man die Scheitelpunkte der Ellipse und kann sie vollständig
konstruieren.
Q
M
U
R
O
P
V
A
M
B
U
R
O
P
V
3. 7