4. Quadratische Gleichungen bei geometrischen Anwendungen ...

4. Quadratische Gleichungen bei geometrischen Anwendungen
Aufgabe:
Bestimme die Schnittpunkte des Kreises mit
Mittelpunkt M(0, 0) und Radius r = 5 mit
der Geraden g: x – y = 1.
Die Koordinaten der Schnittpunkte
erfüllen das folgende Gleichungssystem:
x 2 + y 2 = 25
x - y = 1 (1)
Lösung mit dem Einsetzungsverfahren:
y = -1 + x führt auf die Gleichung
(x + 3)⋅(x - 4) = 0
Setzt man die Lösungen x1 = -3 und x2 = 4
in (1) ein, so ergeben sich die Koordinaten der
Schnittpunkte zu S1(-3, -4) bzw S2(4, 3).
Aufgabe:
Bestimme die Schnittpunkte der Hyperbel
xy = 12 mit der Geraden g: x - 2y - 2 = 0.
Die Koordinaten der Schnittpunkte
erfüllen das folgende Gleichungssystem:
xy = 12 (1)
x - 2y - 2 = 0 (2)
Einsetzungsverfahren: (2')
x = 2y + 2
eingesetzt in (1):
y⋅(2y + 2) = 12 bzw. y⋅(y + 1) = 6
y 2 + y - 6 = (y + 3)⋅(y - 2) = 0
mit den Lösungen
y1 = - 3 eingesetzt in (2') x1 = -4
y2 = 2 eingesetzt in (2') x2 = 6
Die Gerade (2) schneidet die Hyperbel (1) in den beiden Punkten S1(6, 2) und S2(-3, -4)
03.04.2013 Qgl_10_1/ul
9

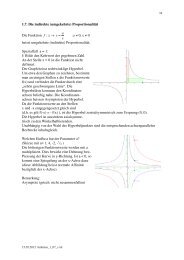
Tangenten an Kegelschnitte
Beim ebenen Schnitt eines geraden Kreiskegels entstehen abgesehen von Spezialfällen
Ellipsen, Parabeln bzw. Hyperbeln.
Vorbereitende Aufgabe:
Bestimme den Parameter q so, dass die quadratische Gleichung x 2 + 6qx - q = 0 genau eine
Lösung hat.
Eine quadratische Gleichung hat genau dann eine einzige Lösung, wenn ihre Diskriminante
den Wert 0 hat.
D = 36q 2 + 4q = 4q⋅(9q + 1) = 0
q = 0 x = 0 ist einzige Lösung
q = - 1 /9 x = 1 /3 ist einzige Lösung.
Tangenten mit vorgegebener Richtung
Aufgabe:
Gegeben ist die Parabel p mit der Gleichung
03.04.2013 Qgl_10_1/ul
y x
1 2
= 4 und die Gerade g mit der
3
Gleichung y = 2 x + q . Schneide die Gerade g mit der Parabel p. Wähle für q die Werte
a) q = - 5 /4 b) q = - 9 /4 c) q = -3.
Die Koordinaten des gemeinsamen Punkte
erfüllen das Gleichungssystem:
(1)
(2)
y = x + q P ist Geradenpunkt
3
2
1 2
= 4 P ist Parabelpunkt
y x
Gleichsetzen führt auf die quadratische
Gleichung
x = x + q bzw. (3)
1 2 3
4 2
1 2 3
4 x − 2 x − q = 0
mit der Diskriminante
D = + q = 0 .
9
4
a) q = - 5 /4
1 2 3 5
4 x − 2 x + 4 = 0
D > 0 x1 = 1, x2 = 5
Die Gerade schneidet die Parabel in zwei verschiedenen Punkten S1(1, 1
25
4 ), S2(5, 4 )
b) q = - 9 /4
1 2 3 9
4 x − 2 x + 4 = 0
D = 0 ( ) 2
x − 3 = 0
x = 3 und mit (2) y = 9
4
Die Gerade berührt die Parabel im Punkt B( 3, 9
4
) g ist Parabeltangente.
1 2 3
c) q = -3
4 x − 2 x + 3 = 0
D < 0
Die Gleichung hat keine reelle Lösung. Die Gerade meidet die Parabel.
10

allg.
Das Problem, eine Parabel mit einer Geraden g: y = mx + q zu schneiden, führt auf eine
quadratische Gleichung mit der Diskriminante D. Es können damit die folgenden Fälle
auftreten:
D > 0 Die Gerade schneidet die Parabel in zwei verschiedenen Punkten.
D = 0 Die Gerade berührt die Parabel, sie ist Tangente
D < 0 Die Gerade meidet die Parabel.
Bemerkung:
Eine entsprechende Aussage gilt auch für die Kegelschnitte Ellipse (insbesondere auch Kreis)
und Hyperbel.
Auch im Ausnahmefall der Parabelachse ergibt sich genau ein Schnittpunkt.
Uebungsaufgabe:
Bestimme q so, dass die Gerade mit der Gleichung y = − 2x
+ q die Parabel mit der Gleichung
1 2
y = − x − x + 3 berührt.
2
7 3
Lösung: q = B 1,
− )
( 2
03.04.2013 Qgl_10_1/ul
2
Tangenten von einem Punkt an einen Kegelschnitt:
Aufgabe:
Lege vom Punkt P(0, -9) die Tangenten an die Parabel
Ansatz für die gesuchten Tangenten:
4 + m = 6
oder
m1 = 2 eingesetzt in (1)
4 + m = − 6 m1 = -10 eingesetzt in (1)
2
y = x − 4x
y = mx − 9
Die y-Koordinaten müssen übereinstimmen
2
mx − 9 = x − 4x
oder
2
x − 4 + m ⋅ x + 9 = 0 (1)
( )
m ist so zu bestimmen, dass (1) genau eine
Lösung besitzt.
( ) 2
D = 4 + m − 36 = 0
2 2
x − 6x + 9 = ( x − 3) = 0 x1 = 3 B1 (3, -3)
2 2
x + 6x + 9 = ( x + 3) = 0 x1 = -3 B2 (-3, 21)
11

Aufgabe:
Lege vom Punkt P(0, 5) die Tangente an den Kreis k mit dem Mittelpunkt M(0, 0) und dem
Radius r = 5 .
2 2
Kreis k: x + y = 5 (1)
Ansatz für die Tangentengleichung
g: y = mx + 5 (2) eingesetzt in (1)
( )
2 2
m x mx
+ 1 + 10 + 20 = 0 (3)
g ist genau dann Tangente, wenn die
Diskriminante von (3) den Wert 0 hat.
03.04.2013 Qgl_10_1/ul
( ) ( )
D = m − ⋅ m + ⋅ = ⋅ m − =
2 2 2
100 4 1 20 20 4 0
Lösungen m1 = 2 und m = -2
m1 = 2 eingesetzt in (3) führt auf die Gleichung
( ) 2
x + x + = ⋅ x + = mit der Lösung x1 = -2 und mit der Gleichung (2) auf die
2
5 20 20 5 2 0
Tangentengleichung y = 2x + 5 und den Berührungspunkt B1(-2, 1).
m2 = -2 ergibt analog den Berührungspunkt B2(2, 1) und die Tangentengleichung
y = − 2x + 5 .
Uebungsaufgabe:
2 2
Welche Tangenten des Kreises k: x + y = 5 sind zur Geraden mit der Gleichung y = 2x
parallel.
Lösung:
2 2
Der Ansatz y = 2x
+ q führt auf die Gleichung 5x + 4qx + q − 5 = 0 mit der Diskriminante
( )
D = q − ⋅ q − =
2 2
16 20 5 0
Die gesuchten Tangenten haben den y-Achsenabschnitt 5 bzw. -5.
12

Uebungsaufgabe:
Lege vom Punkt P(-3, 1) die Tangenten an die Hyperbel mit der Gleichung
Lösung:
Die Koordinaten eines Berührungspunkts B
erfüllen das folgende Gleichungssystem:
(1) y = mx + q B ist Geradenpunkt
1
(2) y = B ist Hyperbelpunkt
x
Damit gilt:
1
2
mx + q = bzw. mx + qx −1
= 0 (3)
x
Die Parameter m und q sind so zu bestimmen,
dass Gleichung (3) genau eine Lösung hat:
(3)
2
D = q + 4m = 0
Die Koordinaten von P erfüllen Gleichung (1):
1 = − 3m + q
q = 3 m + 1 eingesetzt in (3) führt auf:
( 3m
+ 1)
⋅ −1
= 0
2
mx + x
(4)
03.04.2013 Qgl_10_1/ul
1
y = .
x
mit der Diskriminante
2
2
D = ( 3m
+ 1)
+ 4m
= 9m
+ 10m
+ 1
Die Gleichung (4) hat für D = 0 genau eine Lösung:
2
9m + 10m + 1 = 0
Setzt man die Lösungen dieser Gleichung m1 = -1 und m2 = - 1 /9 in die Gleichung (4) ein, so
ergebn sich schliesslich die gesuchten Berührungspunkte B1(-1, -1) und B2(3, 1
3 ).
13