Blatt 5

Aufgabe 20: (Erzwungene Schwingung)
Die Differentialgleichung
dy
dt
Mathematiklabor – 5. Übungsblatt
= d
dt
y1
y2
y2
=
−k(y1 − h(t)) − cy2 − mg
Dr. Jörg-M. Sautter
25.5.2007
beschreibt den zeitlichen Ablauf eines Feder-Schwinger-Systems (vgl. Abb. 1) mit Anregung
h(t). Dabei bezeichnet y1 die vertikale Auslenkung aus der Ruhelage (entspannte Feder),
y2 die vertikale Geschwindigkeit des Schwingers, k = 1 N
m die Federkonstante, c = 0.1 N m die
s
Dämpfungskonstante, m = 0.1 kg die Masse des Schwingers, g = 9.81 m
s2 die Erdbeschleunigung
und
⎧
⎪⎨ 0 t < t1
h(t) = 3
⎪⎩
2 (sin(ω(t − t1))) 2 t1 ≤ t < t2
0 t2 ≤ t
mit t1 = 20 s, t2 = 23 s, ω = π
3
1
s
die vertikale Auslenkung der Anregung in m.
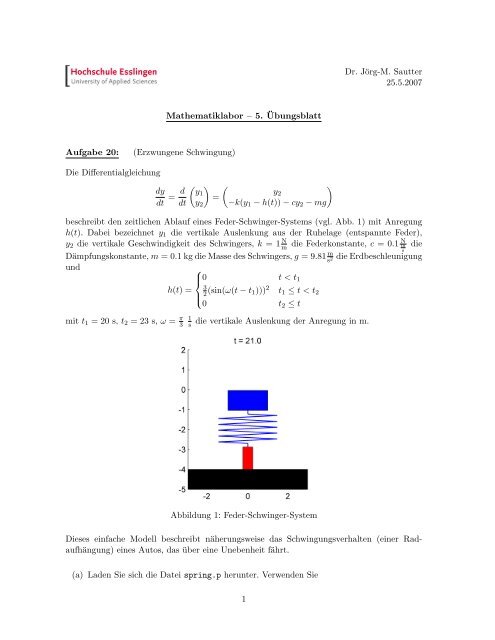
Abbildung 1: Feder-Schwinger-System
Dieses einfache Modell beschreibt näherungsweise das Schwingungsverhalten (einer Radaufhängung)
eines Autos, das über eine Unebenheit fährt.
(a) Laden Sie sich die Datei spring.p herunter. Verwenden Sie
1

spring(0,h-4,0,x,5,2/(x+4-h)^0.5);
zum zeichnen der Feder vom Punkt (0/h − 4) bis zum Punkt (0/x).
(b) Schreiben Sie eine Funktion h=anregung(t,omega,t1,t2), die die vertikale Auslenkung
der Anregung berechnet. Überprüfen Sie Ihre Funktion indem Sie Abbildung 2 erzeugen.
Abbildung 2: Auslenkung der Anregung
(c) Schreiben Sie eine Funktion plotschwinger(t,y1,omega,t1,t2), die das Feder-Schwinger-System
zur Zeit t zeichnet. Dabei bezeichne y1 die Unterkante des Schwingers.
(d) Nun benötigen Sie eine Funktion dy=schwingerode(t,y,m,g,c,k,omega,t1,t2), die
die rechte Seite der Differentialgleichung auswertet.
(e) Lösen Sie die obige Differentialgleichung für
y(0) =
0
0
für 0 ≤ t ≤ 30s. Berechnen Sie die Lösung alle 0.05 Sekunden.
(f) Zeichnen Sie das Feder-Schwinger-System zur Zeit t = 21 s (vgl. Abb. 1).
(g) (Optional!) Simulieren Sie den zeitlichen Verlauf des Systems.
Befehle: cla, fill, hold, if, ode45, pause
2

Aufgabe 21: (Ausgleichsrechnung)
(a) Untersuchen Sie die Lösbarkeit des linearen Gleichungssystems
mit
⎛
⎜
A = ⎝
√1 2
− 1 √
2
√1 5
Ax = b (1)
√1 2
√1 2
√2 5
⎞
⎛
⎟ ⎜
⎠ , b = ⎝
(b) Bestimmen Sie die drei Gleichungssysteme, die durch weglassen einer Gleichung beim
Gleichungssystem (1) entstehen. Berechnen Sie deren Lösungen x1, x2, x3.
(c) Jede einzelne Gleichung des Gleichungssystems (1) definiert eine Gerade. Zeichnen Sie
die Geraden und markieren Sie die Schnittpunkte mit roten Kreisen (vgl. Abb. 3).
Abbildung 3:
(d) Überlegen Sie sich, wie Sie den Abstände von einem Punkt einer Geraden berechnen
können. Schreiben Sie eine Funktion d=sumdist(x), die die Summe der Abstände eines
Punktes x von den obigen drei Geraden berechnet.
(e) Bestimmen Sie den Mittelwert xm der drei Lösungen und vergleichen Sie diesen mit
dem Ergebnis von x0=A\b.
(f) Untersuchen Sie die Residuen d0 = Ax0 − b, dm = Axm − b sowie di = Axi − b für
i = 1, . . . , 3. Interpretieren Sie die Ergebnisse. Welcher Vektor ist am kürzesten?
(g) Berechnen Sie B = A T A und c = A ′ b. Welche Dimensionen haben B und c? Lösen Sie
das Gleichungssystem
Bx = c.
Fällt Ihnen etwas auf?
3
√1 2
√1 2
√3 5
⎞
⎟
⎠ .

Aufgabe 22: (Ausgleichspolynom)
Der Bremsvorgang eines Autos wurde analysiert und die Messung ergab die in Tabelle 1
dargestellten Daten.
(a) Stellen Sie die Daten aus Tabelle 1 in einem Schaubild dar.
(b) Unter der Annahme, dass der Bremsvorgang einer konstanten Beschleunigung unterliegt,
wird dieser durch eine quadratische Funktion
x(t) = a2t 2 + a1t + a0
beschrieben. Bestimmen Sie die Koeffizienten so, dass Gleichung (2) am Besten zu den
Daten in Tabelle 1 passt.
(c) Wie groß ist die als konstant angenommene Bremsbeschleunigung?
(d) Zeichnen Sie das Schaubild der berechneten Bremsfunktion (2) in Ihr Schaubild ein.
(e) Zeichnen Sie ein Geschwindigkeit-Weg-Diagramm.
Zeit Ort
0 0
0.05 1.0343
0.1 1.3488
0.15 2.6291
0.2 2.2365
0.25 2.6409
0.3 3.0615
0.35 3.7259
0.4 4.1869
0.45 5.0955
0.5 4.6164
0.55 5.3629
0.6 5.5346
0.65 5.3386
0.7 6.3885
0.75 6.0686
0.8 6.0881
0.85 6.7539
0.9 6.4331
0.95 6.9359
1 6.6566
Tabelle 1: Weg-Zeit Tabelle
Aktuelle Hinweise zur Vorlesung sowie Begleitmaterial und Übungsblätter finden Sie unter
http://www.hs-esslingen.de/jsautter/mathematiklabor
4
(2)