Wärmelehre
Wärmelehre
Wärmelehre
Sie wollen auch ein ePaper? Erhöhen Sie die Reichweite Ihrer Titel.
YUMPU macht aus Druck-PDFs automatisch weboptimierte ePaper, die Google liebt.
WÄRMELEHRE<br />
1) Temperatur<br />
1.1) Definition<br />
E: Simulation zur Temperatur eines Gases:<br />
http://www.leifiphysik.de/web_ph09/versuche/07brown/applets/bb.html<br />
E: Simulation zu den drei Aggregatszuständen:<br />
http://www.cornelsen.de/physikextra/htdocs/Teilchen2.html<br />
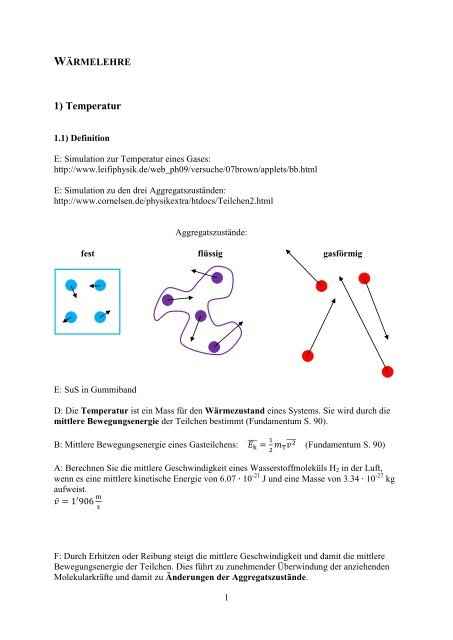
Aggregatszustände:<br />
fest flüssig gasförmig<br />
E: SuS in Gummiband<br />
D: Die Temperatur ist ein Mass für den Wärmezustand eines Systems. Sie wird durch die<br />
mittlere Bewegungsenergie der Teilchen bestimmt (Fundamentum S. 90).<br />
B: Mittlere Bewegungsenergie eines Gasteilchens: (Fundamentum S. 90)<br />
A: Berechnen Sie die mittlere Geschwindigkeit eines Wasserstoffmoleküls H 2 in der Luft,<br />
wenn es eine mittlere kinetische Energie von 6.07 10 -21 J und eine Masse von 3.34 10 -27 kg<br />
aufweist.<br />
F: Durch Erhitzen oder Reibung steigt die mittlere Geschwindigkeit und damit die mittlere<br />
Bewegungsenergie der Teilchen. Dies führt zu zunehmender Überwindung der anziehenden<br />
Molekularkräfte und damit zu Änderungen der Aggregatszustände.<br />
1
1.2) Temperaturskalen<br />
D: Die Celsius-Temperatur bezieht sich auf das Schmelzen (0 °C) und Verdampfen<br />
(100 °C) von Wasser, wobei gilt: [] = °C = Grad Celsius<br />
D: Die Absolute Temperatur T hat ihren Nullpunkt bei ‒273.15 °C,<br />
wobei gilt: [T] = K = Kelvin<br />
‒273.15<br />
0 100 200<br />
, [] = °C<br />
0 273.15 373.15 473.15<br />
T, [T] = K<br />
A: Rechnen Sie 50 °C in K und 50 K in °C um.<br />
323.15 K, ‒223.15 °C<br />
F: Für eine Temperaturdifferenz gilt:<br />
A: Was bedeutet 0 K für die Teilchenbewegung?<br />
S: Der Zusammenhang zwischen der mittleren Geschwindigkeit und der Temperatur eines<br />
Gasteilchens ist: , mit k = 1.38 10 -23 (Boltzmann-Konstante, Fund. S. 90)<br />
A: Berechnen Sie die Temperatur des H 2 -Moleküls aus vorigem Kapitel.<br />
T = 293.24 K ( = 20.09 °C)<br />
2) Wärmeausdehnung<br />
2.1) Längenänderung<br />
E: Eisenkugel erhitzen<br />
E: Stab erhitzen<br />
l<br />
2<br />
l
A: Wovon hängt die Längenänderung ab?<br />
S: (Fundamentum S. 90 und 102)<br />
D: Der Längenausdehnungskoeffizient gibt an, um wie viel sich die Länge eines<br />
bestimmten Körpers bei Temperaturschwankung verändert, wobei gilt:<br />
A: Die Kirchenfeldbrücke (Stahl) ist im Winter (‒5 °C) 230 m lang. Wie lang wäre sie im<br />
Sommer (35 °C)?<br />
= 0.15 m, Sommer = 230.15 m<br />
2.2) Volumenänderung<br />
E: Wasserkugel erhitzen<br />
S: (Fundamentum S. 90 und 102)<br />
D: Der Volumenausdehnungskoeffizient gibt an, um wie viel sich das Volumen eines<br />
bestimmten Körpers bei Temperaturschwankung verändert, wobei gilt:<br />
A: Um wie viel dehnt sich ein Liter Wasser aus, wenn Sie ihn aus dem Kühlschrank (5°C)<br />
genommen und an die Sonne gegeben haben (40°C)?<br />
= 7.35 10 -3 dm 3 (7.35 10 -6 m 3 )<br />
E: „Luftkugel“ erhitzen<br />
S: Alle Körper vergrössern mit steigender Temperatur ihr Volumen bei gleich bleibender<br />
Masse, d.h., ihre Dichte verringert sich (Ausnahmen: Gummi, Wasser).<br />
A: Bei welcher Temperatur hat Wasser seine grösste Dichte ( → „Dichteanomalie“)?<br />
3
3) Wärme Q<br />
3.1) Definition<br />
D: Die Wärme Q ist eine Energieübertragungsgrösse. (Fundamentum S. 91)<br />
3.2) Spezifische Wärmekapazität c p<br />
E: Wasser mit Tauchsieder erhitzen. Dabei wird Wärme vom Sieder auf das Wasser<br />
übertragen. Zeit t bis zum Kochen messen.<br />
m<br />
T<br />
m<br />
T+T<br />
Q<br />
Leistung des Tauchsieders: P = 1‘000 W<br />
Masse des Wassers: m = 0.3 kg<br />
Temperaturdifferenz: T = 80 K (100°C ‒ 20°C)<br />
Gemessene Zeitdauer: t =<br />
A: Wovon hängt die auf das Wasser übertragene Wärme Q ab?<br />
- je grösser Q, desto grösser T (bei gleichem m).<br />
- je grösser Q, desto grösser darf m sein (bei gleichem T)<br />
- ausserdem: materialabhängig<br />
S: Q = c p ∙ m ∙ T (Fundamentum S. 91)<br />
D: Die spezifische Wärmekapazität c p gibt diejenige Energiemenge an, die einem Körper<br />
von 1 kg Masse zugeführt werden muss, um dessen Temperatur um 1 K zu erhöhen.<br />
A: Berechnen Sie für obiges Experiment c p von flüssigem Wasser.<br />
A: Was bedeutet es für das Aufheizen und Abkühlen, wenn ein Körper eine grosse spezifische<br />
Wärmekapazität hat?<br />
A: Was unterscheidet Maritim- von Kontinentalklima?<br />
4
A: In einer Badewanne befinden sich 80 l Wasser von 90 °C. Wie viel Wasser von 20 °C<br />
muss man dazu mischen, so dass das Bad schliesslich eine Temperatur von 37 °C aufweist?<br />
m 1 = 249 kg<br />
3.3) Änderung der Aggregatszustände<br />
B: Wasser<br />
sublimieren<br />
schmelzen<br />
verdampfen<br />
fest 0 °C flüssig 100 °C gasförmig<br />
erstarren<br />
kondensieren<br />
resublimieren<br />
3.3.1) Schmelzen und Erstarren<br />
D: Die Schmelztemperatur f ist diejenige Temperatur, bei der sich die kristalline Struktur<br />
eines Festkörpers auflöst.<br />
D: Die spezifische Schmelzwärme L f ist diejenige Energiemenge, die einem Körper von 1 kg<br />
Masse zugeführt werden muss, um diesen zu schmelzen.<br />
S: Q = L f ∙ m<br />
A: Welche Wärmemenge ist nötig, um 800 kg Eisen zu schmelzen?<br />
Q = 2.216 ∙ 10 8 J (222 MJ)<br />
A: Wie obige Aufgabe, aber mit Ausgangstemperatur von 20°C<br />
Q total = Q erwärmen + Q schmelzen = 767 MJ<br />
5
D: Die Erstarrungstemperatur ist diejenige Temperatur, bei der sich die kristalline Struktur<br />
eines Festkörpers bildet. Sie ist gleich hoch wie die Schmelztemperatur.<br />
D: Die spezifische Erstarrungswärme ist diejenige Energiemenge, die einem Körper der<br />
Masse 1 kg entzogen werden muss, um diesen erstarren zu lassen. Sie ist gleich gross wie die<br />
spezifische Schmelzwärme.<br />
S: Erstarrt ein Körper, wird Energie frei!<br />
E: Wärmebeutel<br />
E: Eis-Wasser-Gemisch erhitzen, Temperatur ständig messen<br />
S: Weder beim Schmelzen noch beim Erstarren ändert sich die Temperatur eines Körpers.<br />
3.3.2) Verdampfen und Kondensieren<br />
D: Die Siedetemperatur V ist diejenige Temperatur, bei der eine Flüssigkeit gasförmig<br />
wird.<br />
D: Die spezifische Verdampfungswärme L V ist diejenige Energiemenge, die einem Körper<br />
von 1 kg Masse zugeführt werden muss, um diesen zu verdampfen.<br />
S: Q = L V ∙ m (Fundamentum S. 91 und 102)<br />
A: Welche Wärmemenge ist nötig, um 0.8 kg Wassereis von -10°C vollständig in<br />
Wasserdampf umzuwandeln?<br />
Q total = 2.42 MJ<br />
D: Die Kondensationstemperatur ist diejenige Temperatur, bei der sich Gas in Flüssigkeit<br />
verwandelt. Sie ist gleich hoch wie die Siedetemperatur.<br />
D: Die spezifische Kondensationswärme ist diejenige Energiemenge, die einem Körper der<br />
Masse 1 kg entzogen werden muss, um diesen zu verflüssigen. Sie ist gleich gross wie die<br />
spezifische Verdampfungswärme.<br />
S: Kondensiert ein Gas, wird Energie frei!<br />
B: Quellwolken (http://www.youtube.com/watch?v=ll3i35UrNEw&feature=related)<br />
E: Wasser sieden, Temperatur ständig messen<br />
S: Weder beim Verdampfen noch beim Kondensieren ändert sich die Temperatur eines<br />
Körpers.<br />
6
3.3.3) Verdunsten<br />
A: Wie sieht die Häufigkeitsverteilung der Geschwindigkeiten der Wassermoleküle in einer<br />
Pfütze von 20 °C aus?<br />
Anzahl Moleküle n<br />
Molekülgeschwindigkeit v, [v] =<br />
F: Die Häufigkeiten der Geschwindigkeiten folgen einer so genannten Maxwell-Verteilung,<br />
deren Maximum der mittleren Geschwindigkeit aller Moleküle (s. Seite 1) und damit der<br />
Temperatur der Pfütze entspricht.<br />
A: Weshalb kann sich diese Wasserpfütze auch bei 20°C allmählich in Wasserdampf<br />
umwandeln?<br />
F: Auch bei 20°C gibt es Moleküle, deren Geschwindigkeit einer Temperatur über 100 °C<br />
entspricht. Diese können die Flüssigkeit verlassen und kehren nicht mehr zurück.<br />
A: Was passiert mit der Temperatur der verbleibenden Flüssigkeit?<br />
F: Verliert die Pfütze ständig seine schnellsten Teilchen, sinkt die mittlere Geschwindigkeit<br />
und damit die Temperatur → „Verdunstungskälte“<br />
7
A: Weshalb haben Sie kalt, wenn Sie im Sommer aus der Aare steigen, obwohl die<br />
Lufttemperatur 35°C beträgt?<br />
E: Alkohol auf Haut<br />
A: Wie lange dauert dieser Kühlungsprozess?<br />
A: Was begünstigt den Verdunstungsprozess?<br />
B für Verdunstungskälte: Schwitzen (Abbildung 1)<br />
Abbildung 1 Abbildung 2<br />
3.3.4) Sublimieren und Resublimieren<br />
A: Was ist Trockeneis und woher hat es seinen Namen?<br />
E: Trockeneis (Abbildung 2)<br />
A: Weshalb muss man den Kühlschrank ab und zu enteisen?<br />
B für Resublimation: Eisblumen an schlecht isolierten Fenstern (Abbildung 3)<br />
Abbildung 3 Abbildung 4<br />
8
3.4) Luftfeuchtigkeit<br />
A: Wo ist das flüssige Wasser nach dem Verdunsten bzw. Verdampfen?<br />
F: Beim Verdunsten oder Verdampfen nimmt die Luft das Wasser auf. Dabei ändern die H 2 O-<br />
Moleküle ihren chemischen Aufbau nicht.<br />
D: Die Luftfeuchtigkeit gibt den gasförmigen Wassergehalt der Luft an<br />
(Fundamentum S. 91).<br />
D: Die absolute Luftfeuchtigkeit a gibt an, wie viele Gramm Wasser in einem Kubikmeter<br />
Luft enthalten ist.<br />
F: a = ; [ a ] = wobei: V = Volumen der Luft<br />
A: In der Luft des Schulzimmers (4 m × 8 m × 12 m) sind 4 Liter Wasser enthalten.<br />
Berechnen Sie die absolute Luftfeuchtigkeit.<br />
a = 10.4<br />
A: Warum ist es in der Sauna dunstig (Abbildung 4, S. 8)?<br />
D: Die Sättigungsdampfdichte s gibt an, wie viele Gramm Wasser ein Kubikmeter Luft<br />
maximal aufnehmen kann.<br />
F: Wird die Sättigungsdampfdichte überschritten, kondensiert das Wasser wieder aus<br />
(Wolken, Nebel, Tau).<br />
A: Wovon hängt die Sättigungsdampfdichte ab (Fundamentum S. 103)?<br />
A: Wie viel Wasser könnte unser Schulzimmer bei 20 °C maximal aufnehmen?<br />
m = 6‘651 g (6.7 Liter)<br />
D: Die relative Luftfeuchtigkeit r gibt an, zu wie viel Prozent die Luft mit Wasser<br />
gesättigt ist.<br />
S:<br />
A: Berechnen Sie die relative Luftfeuchtigkeit in unserem Schulzimmer ( = 20 °C).<br />
r = 60 %<br />
A: Was passiert mit der absoluten und was mit der relativen Luftfeuchtigkeit, wenn die Luft<br />
im Schulzimmer aufgeheizt bzw. abgekühlt wird?<br />
F: Ist in der Luft die Sättigungsdampfdichte erreicht, herrscht 100 % rel. Luftfeuchtigkeit.<br />
9
4) Wärmetransport<br />
F: Wärme kann auf drei verschiedene Arten von einem Körper auf einen anderen übertragen<br />
werden:<br />
4.1) Wärmeleitung<br />
E: Verschiedene gleichlange Stäbe erhitzen<br />
F: Wärme wandert von selbst durch ein Material (Nachbarmoleküle werden angestossen).<br />
Q<br />
S: Bei der Wärmeleitung wird die Energie ohne Materietransport weitergeleitet.<br />
E: Eis schmilzt in kochendem Wasser nicht sofort.<br />
E: Wassertropfen verdampfen nicht sofort sondern „schweben“ auf der heissen Herdplatte, da<br />
der Wasserdampf eine isolierende Schicht bildet (Leidenfrostsches Phänomen):<br />
flüssiges<br />
S: Metalle sind gute, Flüssigkeiten und Gase schlechte Wärmeleiter.<br />
10
A: Weshalb isolieren Eisbärfell (links) und Styropor (rechts) gut?<br />
D: Die Wärmeleitfähigkeit gibt an, wie gut ein Material die Wärme leitet.<br />
(Fundamentum S. 102)<br />
S: Die pro Zeit t durch ein Material der Querschnittsfläche A, der Schichtdicke x und der<br />
Wärmeleitfähigkeit geleitete Wärmemenge Q ist (Fundamentum S. 91):<br />
T 1<br />
T 2 < T 1<br />
<br />
<br />
<br />
<br />
A<br />
<br />
<br />
x<br />
A: Der Boden einer runden Aluminiumpfanne (Durchmesser 20 cm) ist 6 mm dick. Die 20 °C<br />
warme Pfanne wird auf eine 80 °C heisse Herdplatte gestellt. Wie viel Wärme wird pro<br />
Sekunde ins Pfanneninnere geleitet?<br />
Q = 75 kJ<br />
4.2) Konvektion<br />
E: Handpropeller, Kerzenkarussell<br />
F: Warme aufsteigende Luft treibt<br />
Propeller an.<br />
11
E: Wasserzirkulation im Rechteckrohr<br />
B: „kochende“ Sonnenoberfläche (http://www.uni-sw.gwdg.de/~bruno/APOD/apod.html)<br />
S: Im Gegensatz zur Wärmeleitung strömt bei der Konvektion die Energie mit der Materie<br />
mit.<br />
A: Weshalb hat es Rippen an Motorzylindern und weshalb hat man doppel- oder gar<br />
dreifachverglaste Fenster?<br />
4.3) Wärmestrahlung<br />
B: Von der Sonne wird Energie durch das Vakuum hindurch zur Erde abgestrahlt.<br />
E: 2 Aluspiegel mit einer Wärmequelle im einen Brennpunkt<br />
Vakuum<br />
S: Wärmestrahlung ist Energietransport ohne Materie.<br />
12
D: Die Emissionszahl gibt an, wie stark die Oberfläche eines Materials Wärme abstrahlt.<br />
S: Die von einem strahlenden Körper mit Oberfläche A und Emissionszahl pro Zeiteinheit<br />
t abgegebene Wärmemenge Q ist (Fundamentum S. 91 und 103):<br />
<br />
<br />
A: Wie viel Energie strahlt ein Mensch (A = 2 m 2 , = 30 °C) in einer Sekunde ab?<br />
Q = 938.58 J<br />
A: Wie wird bei einer Thermosflasche der Wärmeverlust verhindert?<br />
A: Weshalb streuen Bauern im Frühling schwarze Asche auf den weissen Schnee?<br />
F: Körper mit schwarzer Oberfläche können mehr Energie aufnehmen (absorbieren) als<br />
Körper mit weisser Oberfläche. Sie strahlen aber auch stärker ab.<br />
A: Wie kommt es zum Treibhauseffekt?<br />
<br />
<br />
<br />
<br />
Sichtbares Licht von der Sonne hat sein Strahlungsmaximum bei Gelb (600 nm<br />
Wellenlänge).<br />
Es wird weniger durch die Erdatmosphäre und mehr durch die Erdoberfläche<br />
absorbiert.<br />
Die Wärmeabstrahlung der nunmehr aufgeheizten Erdoberfläche hat ihr Maximum im<br />
Infrarot-Bereich (800 nm Wellenlänge).<br />
Und diese Strahlung wird von der Erdatmosphäre stark absorbiert → Aufheizen der<br />
Atmosphäre (beschleunigt durch diverse Gase).<br />
13
5.) Hauptsätze der <strong>Wärmelehre</strong><br />
5.1) Innere Energie U<br />
F: Moleküle können noch andere Bewegungen als reine Verschiebungen vollführen<br />
(Schwingungen, Rotationen, …).<br />
B: Schwingungen eines dreiatomigen linearen Moleküls<br />
D: Die innere Energie U ist die gesamte kinetische Energie der sich bewegenden Teilchen in<br />
einem Körper.<br />
F: Je grösser die innere Energie eines Körpers desto grösser ist auch seine Temperatur.<br />
F: Der Energieerhaltungssatz aus der Mechanik (s. „Mechanik“, Kap. 4.4) muss somit<br />
ergänzt werden.<br />
S:<br />
F: Umwandlungen von einer Energieform in eine andere sind auch hier möglich.<br />
B: Dampfmaschine wandelt innere Energie in kinetische Energie um.<br />
14
5.2) Erster Hauptsatz der <strong>Wärmelehre</strong><br />
A: Wie kann die innere Energie U eines Körpers erhöht werden?<br />
E: Metall durch Flamme oder „Schmieden“ aufheizen<br />
U<br />
U + U<br />
U<br />
U + U<br />
F: Die innere Energie U kann durch Zuführen von Wärme und/oder Arbeit erhöht werden.<br />
1. Hauptsatz: Fügen wir einem Körper die Wärmemenge Q und die Arbeit W zu, so erhöht<br />
sich seine innere Energie U um U.<br />
S: (Fundamentum S. 92)<br />
F: Es gibt alternative Formulierungen des 1. Hauptsatzes:<br />
<br />
<br />
<br />
In einem energetisch abgeschlossenen System bleibt die Gesamtenergie konstant.<br />
Energie kann nicht erzeugt, sondern nur umgewandelt und übertragen werden.<br />
Es gibt kein Perpetuum Mobile 1. Art.<br />
D: Ein Perpetuum Mobile 1. Art ist eine Maschine, die ohne Antrieb ständig läuft.<br />
B: Dampfmaschine, die Arbeit verrichtet ohne aufgeheizt zu werden.<br />
B für Perpetua Mobilia aus der Mechanik und Hydrodynamik<br />
15
5.3) Zweiter Hauptsatz der <strong>Wärmelehre</strong><br />
E: Zwei identische Metallklötze von unterschiedlichen Temperaturen werden<br />
zusammengefügt.<br />
m 1 = 1 kg<br />
1 = 80 °C<br />
m 2 = 1 kg<br />
2 = 20 °C<br />
Q<br />
m 3 =<br />
3 =<br />
A: Was passiert?<br />
F: Der wärmere Klotz wird solange Wärme an den kälteren Klotz abgeben, bis beide die<br />
gleiche Temperatur haben.<br />
2. Hauptsatz: Wärme strömt immer selbständig von Orten höherer Temperatur zu Orten mit<br />
niedrigerer Temperatur, nie umgekehrt (Fundamentum S. 92).<br />
F: Auch hier gibt es alternative Formulierungen:<br />
<br />
<br />
Abgeschlossene Systeme streben einen Zustand maximaler Unordnung bzw. grösster<br />
Wahrscheinlichkeit an (Prinzip der maximalen Entropie).<br />
Es gibt kein Perpetuum Mobile 2. Art.<br />
D: Ein Perpetuum Mobile 2. Art ist eine Maschine, die Wärme vollständig in Arbeit<br />
umwandeln kann.<br />
B: Dampfmaschine, die ohne Wärmeverlust 100% der Wärme in Arbeit verwandeln kann.<br />
F: Bei jeder Maschine, die Energien umwandelt, gibt es „Energieverluste“ (Abwärme,<br />
Reibungsverluste, etc.).<br />
B: Benzinmotor wandelt chemisch gespeicherte Energie in mechanische Energie um. Dabei<br />
werden der Motor, die Kühlflüssigkeit, die Lager, die Auspuffgase, die Räder etc. aufgeheizt.<br />
16
6) Wirkungsgrade<br />
6.1) Wärmekraftmaschinen WKM<br />
A: Was passiert, wenn die Luft in einer verschlossenen Spritze aufgeheizt wird?<br />
F: Das Gas verrichtet Arbeit wegen der Wärmeausdehnung.<br />
A: Was ist nötig, um daraus eine zyklisch arbeitende Maschine bauen zu können?<br />
A: Erklären Sie das Prinzip einer Dampfmaschine nach James Watt.<br />
Dampfkessel<br />
Pumpkolben<br />
Kondensator<br />
Einlassventil<br />
Arbeitszylinder<br />
Auslassventil<br />
17
F: Eine Wärmekraftmaschine (WKM) entzieht einem heissen Energiereservoir Wärme,<br />
welche sie in Arbeit umwandelt. Dies gelingt aber gemäss 2. Hauptsatz der <strong>Wärmelehre</strong> nicht<br />
zu 100%, denn es wird ein Teil der entzogenen Wärme an ein kaltes Energiereservoir<br />
abgegeben.<br />
A: WKM-Schema gemäss Fundamentum S. 92. Wo ist was bei der Dampfmaschine?<br />
T W : T K :<br />
Q W : Q K :<br />
WKM: W N :<br />
D: Der reale Wirkungsgrad real (Wirkungsgrad einer real existierenden Maschine) ist das<br />
Verhältnis von Nutzarbeit W N zu Antriebswärme Q W (Fundamentum S. 92):<br />
S:<br />
A: Eine Dampfmaschine leistet 4.5 kJ Arbeit aus einer Wärmemenge von 22kJ. Berechnen<br />
Sie den realen Wirkungsgrad.<br />
real = 0.20 (oder 20%)<br />
A: Wie gross wäre der reale Wirkungsgrad, wenn die Maschine entweder keine Nutzarbeit<br />
leistet oder sämtliche Antriebswärme in Nutzarbeit umwandeln könnte?<br />
real = 0 bzw. 1<br />
A: Ist bei einer realen Maschine ein Wirkungsrad von 1 überhaupt möglich?<br />
F: Gemäss 2. Hauptsatz der <strong>Wärmelehre</strong> gibt es immer Abwärme Q K (Fundamentum S. 92)<br />
D: Der theoretische Wirkungsgrad Carnot (maximaler theoretischer Wirkungsgrad einer<br />
idealen Maschine) ist das Verhältnis aus der Temperaturdifferenz von Antriebswärme zu<br />
Abwärme (T W – T K ) und der Temperatur der Antriebswärme:<br />
S:<br />
A: Der Dampf einer Dampfmaschine habe eine Temperatur von 250 °C, die an die Umwelt<br />
abgegebene Abluft eine Temperatur von 50 °C. Berechnen Sie den theoretischen<br />
Wirkungsgrad.<br />
Carnot = 0.38 (oder 38%)<br />
18
A: In welcher Situation ist der theoretische Wirkungsgrad 0 bzw. 1?<br />
F: Je grösser die Temperaturdifferenz zwischen den beiden Wärmereservoirs, desto grösser ist<br />
der theoretische Wirkungsgrad.<br />
A: Wie funktionieren Verbrennungsmotoren?<br />
E: Neufelder Tischbombe<br />
F: Durch Verbrennung von Benzin-Luftgemisch erzeugte Wärme lässt Luft<br />
schlagartig expandieren.<br />
A: Erklären Sie das Prinzip eines Vier- und des Zweitaktmotors<br />
(http://upload.wikimedia.org/wikipedia/commons/a/a6/4-Stroke-Engine.gif,<br />
http://upload.wikimedia.org/wikipedia/commons/3/33/Two-Stroke_Engine.gif).<br />
19
6.2) Wärmepumpe WP<br />
F: Eine WKM entnimmt einem heisseren Wärmereservoir Arbeitswärme und überträgt die<br />
Abwärme in ein kälteres Wärmereservoir. Dabei wird Nutzarbeit geleistet.<br />
A: Was muss geschehen, wenn eine Maschine dem kälteren Reservoir Wärme entziehen und<br />
in ein heisseres Reservoir abgeben will (obwohl dies auf den ersten Blick nicht sehr sinnvoll<br />
erscheint)?<br />
F: Eine Wärmepumpe kehrt die Energieflüsse um („rückwärts“ laufende WKM)<br />
B: Kühlschrank<br />
A: WP-Schema gemäss Fundamentum S. 92. Wo ist was beim Kühlschrank?<br />
T W : T K :<br />
Q W : Q K :<br />
WP: W A :<br />
F: Die Nutzarbeit W N wurde zur Antriebsarbeit W A , die Antriebswärme Q W zur Heizwärme<br />
Q W und die Abwärme Q K zur Umweltwärme Q K .<br />
20
A: Was passiert mit dem realen Wirkungsgrad einer WP (Fundamentum S. 92)?<br />
S:<br />
A: Eine Wärmepumpe führt der Zimmerluft eine Wärmemenge von 2 MJ unter einem<br />
Arbeitsaufwand von 560 kJ zu. Berechnen Sie den realen Wirkungsgrad.<br />
real = 3.57 (oder 357 %)<br />
A: In welcher Situation ist der reale Wirkungsgrad minimal?<br />
A: Wann wird er grösser?<br />
F: Der reale Wirkungsgrad ist eine Zahl, die grösser als 1 ist.<br />
A: Was passiert mit dem theoretischen Wirkungsgrad?<br />
S:<br />
A: Ein Kühlschrank weist im Gefrierfach eine Temperatur von -15 °C auf. Die Küchenluft<br />
betrage 22 °C. Berechnen Sie den theoretischen Wirkungsgrad.<br />
Carnot = 7.98 (oder 798 %)<br />
A: Was passiert, wenn das kältere Wärmereservoir eine Temperatur von 0K hätte?<br />
F: Je grösser die Temperaturdifferenz zwischen den beiden Wärmereservoirs, desto kleiner ist<br />
der theoretische Wirkungsgrad.<br />
F: Nicht nur die Energieflüsse sondern auch die Wirkungsgrade werden invertiert.<br />
21