Nachtrag zu Mittelwerten und MaÃen der Dispersion ... - IPdS in Kiel
Nachtrag zu Mittelwerten und MaÃen der Dispersion ... - IPdS in Kiel
Nachtrag zu Mittelwerten und MaÃen der Dispersion ... - IPdS in Kiel
Erfolgreiche ePaper selbst erstellen
Machen Sie aus Ihren PDF Publikationen ein blätterbares Flipbook mit unserer einzigartigen Google optimierten e-Paper Software.
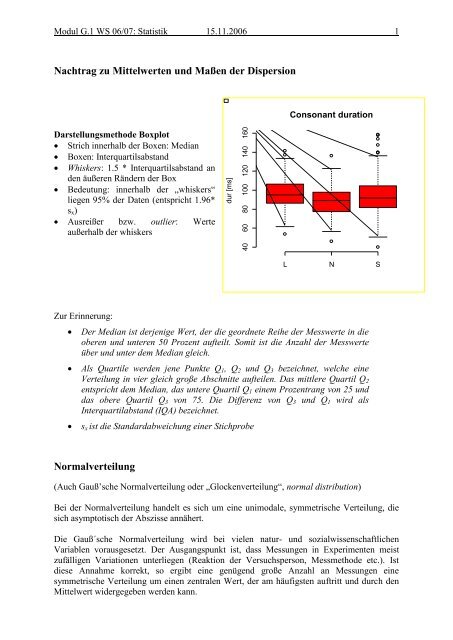
dur [ms]<br />
40 60 80 100 120 140 160<br />
Modul G.1 WS 06/07: Statistik 15.11.2006 1<br />
<strong>Nachtrag</strong> <strong>zu</strong> <strong>Mittelwerten</strong> <strong>und</strong> Maßen <strong>der</strong> <strong>Dispersion</strong><br />
Consonant duration<br />
Darstellungsmethode Boxplot<br />
Strich <strong>in</strong>nerhalb <strong>der</strong> Boxen: Median<br />
Boxen: Interquartilsabstand<br />
Whiskers: 1.5 * Interquartilsabstand an<br />
den äußeren Rän<strong>der</strong>n <strong>der</strong> Box<br />
Bedeutung: <strong>in</strong>nerhalb <strong>der</strong> „whiskers“<br />
liegen 95% <strong>der</strong> Daten (entspricht 1.96*<br />
s x )<br />
Ausreißer bzw. outlier: Werte<br />
außerhalb <strong>der</strong> whiskers<br />
L N S<br />
Zur Er<strong>in</strong>nerung:<br />
<br />
<br />
<br />
Der Median ist <strong>der</strong>jenige Wert, <strong>der</strong> die geordnete Reihe <strong>der</strong> Messwerte <strong>in</strong> die<br />
oberen <strong>und</strong> unteren 50 Prozent aufteilt. Somit ist die Anzahl <strong>der</strong> Messwerte<br />
über <strong>und</strong> unter dem Median gleich.<br />
Als Quartile werden jene Punkte Q 1 , Q 2 <strong>und</strong> Q 3 bezeichnet, welche e<strong>in</strong>e<br />
Verteilung <strong>in</strong> vier gleich große Abschnitte aufteilen. Das mittlere Quartil Q 2<br />
entspricht dem Median, das untere Quartil Q 1 e<strong>in</strong>em Prozentrang von 25 <strong>und</strong><br />
das obere Quartil Q 3 von 75. Die Differenz von Q 3 <strong>und</strong> Q 1 wird als<br />
Interquartilabstand (IQA) bezeichnet.<br />
s x ist die Standardabweichung e<strong>in</strong>er Stichprobe<br />
Normalverteilung<br />
(Auch Gauß’sche Normalverteilung o<strong>der</strong> „Glockenverteilung“, normal distribution)<br />
Bei <strong>der</strong> Normalverteilung handelt es sich um e<strong>in</strong>e unimodale, symmetrische Verteilung, die<br />
sich asymptotisch <strong>der</strong> Abszisse annähert.<br />
Die Gauß´sche Normalverteilung wird bei vielen natur- <strong>und</strong> sozialwissenschaftlichen<br />
Variablen vorausgesetzt. Der Ausgangspunkt ist, dass Messungen <strong>in</strong> Experimenten meist<br />
<strong>zu</strong>fälligen Variationen unterliegen (Reaktion <strong>der</strong> Versuchsperson, Messmethode etc.). Ist<br />
diese Annahme korrekt, so ergibt e<strong>in</strong>e genügend große Anzahl an Messungen e<strong>in</strong>e<br />
symmetrische Verteilung um e<strong>in</strong>en zentralen Wert, <strong>der</strong> am häufigsten auftritt <strong>und</strong> durch den<br />
Mittelwert wi<strong>der</strong>gegeben werden kann.
Modul G.1 WS 06/07: Statistik 15.11.2006 2<br />
Johnson (2004, p.14) beschreibt diese mittlere Tendenz als das <strong>zu</strong>gr<strong>und</strong>eliegende Merkmal,<br />
das wir bei Experimenten herausf<strong>in</strong>den wollen, das aber durch <strong>zu</strong>fällige Fehler „verfälscht“<br />
wird. Für die <strong>zu</strong>fälligen Fehler gilt, dass die größeren Abweichungen seltener auftreten,<br />
weshalb sich die Verteilung <strong>zu</strong> den Rän<strong>der</strong>n h<strong>in</strong> an null annähert.<br />
Die beson<strong>der</strong>e Bedeutung <strong>der</strong> Normalverteilung beruht unter an<strong>der</strong>em auf dem zentralen<br />
Grenzwertsatz, <strong>der</strong> besagt, dass e<strong>in</strong>e Summe von n unabhängigen, identisch verteilten<br />
Zufallsvariablen im Grenzwert<br />
normalverteilt ist. Das bedeutet, dass man<br />
Zufallsvariablen dann als normalverteilt ansehen kann, wenn sie durch Überlagerung e<strong>in</strong>er<br />
großen Zahl von E<strong>in</strong>flüssen entstehen, wobei jede e<strong>in</strong>zelne E<strong>in</strong>flussgröße e<strong>in</strong>en im Verhältnis<br />
<strong>zu</strong>r Gesamtsumme unbedeutenden Beitrag liefert.<br />
Beispiel:<br />
Auf e<strong>in</strong>er Hühnerfarm mit sehr vielen Hühnern werden e<strong>in</strong>e Woche lang die e<strong>in</strong>zelnen Eier<br />
gewogen. Def<strong>in</strong>ieren wir die Zufallsvariable X: Gewicht e<strong>in</strong>es Eis <strong>in</strong> Gramm. Es stellt sich<br />
heraus, dass e<strong>in</strong> Ei im Durchschnitt 50 g wiegt. Der Erwartungswert EX (o<strong>der</strong> auch µ) ist<br />
daher 50. Außerdem sei bekannt, dass die Varianz s 2 (x) = 25 g 2 beträgt. Man kann die<br />
Verteilung des Gewichts annähernd wie <strong>in</strong> <strong>der</strong> Grafik darstellen. Man sieht, dass sich die<br />
meisten Eier <strong>in</strong> <strong>der</strong> Nähe des Erwartungswerts 50 bef<strong>in</strong>den <strong>und</strong> dass die Wahrsche<strong>in</strong>lichkeit,<br />
sehr kle<strong>in</strong>e o<strong>der</strong> sehr große Eier <strong>zu</strong> erhalten, sehr kle<strong>in</strong> wird. Wir haben hier e<strong>in</strong>e<br />
Normalverteilung vor uns. Sie ist typisch für Zufallsvariablen, die sich aus sehr vielen<br />
verschiedenen E<strong>in</strong>flüssen <strong>zu</strong>sammensetzen, die man nicht mehr trennen kann, z.B. Gewicht<br />
des Huhns, Alter, Ges<strong>und</strong>heit, Standort, Vererbung usw.<br />
Die Normalverteilung ist symmetrisch bezüglich μ. Die Verteilung P(X ≤ a) von X ist die<br />
Fläche unter dem Graph <strong>der</strong> Dichtefunktion. Sie wird bezeichnet als<br />
Beispielsweise beträgt die Wahrsche<strong>in</strong>lichkeit, dass e<strong>in</strong> Ei höchstens 55 g wiegt, 0,8413. Das<br />
entspricht <strong>der</strong> roten Fläche <strong>in</strong> <strong>der</strong> Abbildung.
Modul G.1 WS 06/07: Statistik 15.11.2006 3<br />
Mit Standardabweichung = σ <strong>und</strong> Erwartungswert = µ<br />
Der Erwartungswert (selten <strong>und</strong> doppeldeutig Mittelwert) ist e<strong>in</strong> Begriff <strong>der</strong> Stochastik. Der<br />
Erwartungswert μ e<strong>in</strong>er Zufallsvariablen (X) ist jener Wert, <strong>der</strong> sich (<strong>in</strong> <strong>der</strong> Regel) bei<br />
oftmaligem Wie<strong>der</strong>holen des <strong>zu</strong>gr<strong>und</strong>e liegenden Experiments als Mittelwert <strong>der</strong> Ergebnisse<br />
ergibt. Er bestimmt die Lokalisation (Lage) e<strong>in</strong>er Verteilung <strong>und</strong> ist vergleichbar mit dem<br />
empirischen arithmetischen Mittel e<strong>in</strong>er Häufigkeitsverteilung <strong>in</strong> <strong>der</strong> deskriptiven Statistik.<br />
Das Gesetz <strong>der</strong> großen Zahlen sichert <strong>in</strong> vielen Fällen <strong>zu</strong>, dass <strong>der</strong> Stichprobenmittelwert bei<br />
wachsen<strong>der</strong> Stichprobengröße gegen den Erwartungswert konvergiert.<br />
Eigenschaften:<br />
Datenreduktion: Mit den beiden Kenngrößen μ <strong>und</strong> σ kann die Wahrsche<strong>in</strong>lichkeit für das<br />
Auftreten e<strong>in</strong>zelner Messwerte vorhergesagt werden.<br />
Die Fläche unterhalb <strong>der</strong> Kurve ist immer 1, d.h. Normalverteilungen mit e<strong>in</strong>em<br />
Mittelwert, <strong>der</strong> e<strong>in</strong>e ger<strong>in</strong>ge Häufigkeit aufweist, haben e<strong>in</strong>e große Standardabweichung<br />
(„flach <strong>und</strong> breit“) <strong>und</strong> umgekehrt („spitz <strong>und</strong> schmal“)<br />
Dichte (density): gibt die Wahrsche<strong>in</strong>lichkeit an, dass e<strong>in</strong> Maß sehr nah an e<strong>in</strong>em<br />
Messwert liegt. Wahrsche<strong>in</strong>lichkeiten liegen zwischen 0 <strong>und</strong> 1 mit steigen<strong>der</strong><br />
Wahrsche<strong>in</strong>lichkeit. Durch die Def<strong>in</strong>ition <strong>der</strong> Funktionsgleichung ist es möglich, das<br />
Integral, die Fläche, unter <strong>der</strong> Kurve, <strong>zu</strong> berechnen. Mit dieser Fläche kann man die<br />
Intervalle bestimmen, <strong>in</strong> denen gewisse Prozentanteile <strong>der</strong> Stichprobe mit hoher<br />
Wahrsche<strong>in</strong>lichkeit enthalten s<strong>in</strong>d. E<strong>in</strong>e Dichtefunktion, Wahrsche<strong>in</strong>lichkeitsdichte o<strong>der</strong><br />
Wahrsche<strong>in</strong>lichkeitsdichtefunktion (WDF o<strong>der</strong> pdf von engl. probability density function)<br />
dient <strong>in</strong> <strong>der</strong> Mathematik <strong>der</strong> Beschreibung von Wahrsche<strong>in</strong>lichkeitsverteilungen<br />
Bei normalverteilten Daten liegen 68,28% <strong>der</strong> Daten <strong>in</strong>nerhalb e<strong>in</strong>es Bereiches von ±<br />
1Standardabweichung <strong>und</strong> 95,44 % im Bereich von ± 2 SD<br />
Im statistischen S<strong>in</strong>ne normale Daten liegen zwischen -1,96 * SD <strong>und</strong> +1,96*SD. Alle<br />
außerhalb dieser 95% Marke liegenden Daten s<strong>in</strong>d Ausreißer.
Density<br />
0.002 0.004 0.006 0.008 0.010 0.012<br />
Modul G.1 WS 06/07: Statistik 15.11.2006 4<br />
Die Wahrsche<strong>in</strong>lichkeiten <strong>der</strong> e<strong>in</strong>zelnen Ausprägungen e<strong>in</strong>er stetigen Zufallsvariablen können<br />
(im Gegensatz <strong>zu</strong>m diskreten Fall <strong>der</strong> Wahrsche<strong>in</strong>lichkeitsfunktion) nicht angegeben werden,<br />
denn die Wahrsche<strong>in</strong>lichkeiten für jede e<strong>in</strong>zelne Ausprägung müssen streng genommen 0<br />
gesetzt werden. Es lassen sich nur Wahrsche<strong>in</strong>lichkeiten f(x)dx dafür angeben, dass die Werte<br />
<strong>in</strong>nerhalb e<strong>in</strong>es Intervalls dx um x liegen. Die Funktion f(x) heißt dann Dichtefunktion. Die<br />
Wahrsche<strong>in</strong>lichkeit, dass die Zufallsvariable Werte zwischen a <strong>und</strong> b annimmt, wird dann<br />
allgeme<strong>in</strong> def<strong>in</strong>iert als das Integral über diese Funktion mit den Integrationsgrenzen a <strong>und</strong> b.<br />
Beispielsweise fragt man nicht, wie viele Personen exakt 1,75 Meter groß s<strong>in</strong>d, son<strong>der</strong>n z. B.,<br />
wie viele Personen zwischen 1,75 <strong>und</strong> 1,76 m groß s<strong>in</strong>d. Denn die Wahrsche<strong>in</strong>lichkeit, dass<br />
e<strong>in</strong>e Person auf beliebig viele Nachkommastellen genau 1,75 Meter groß ist, ist theoretisch<br />
<strong>und</strong> praktisch gleich Null (daraus folgt: Nullmenge).<br />
Beispiel:<br />
Der HAWIE (Hamburg-Wechsler-Intelligenztest für Erwachsene) besitzt e<strong>in</strong>en Mittelwert<br />
von x = 100 IQ-Punkte <strong>und</strong> e<strong>in</strong>e Standardabweichung von sx=15 Punkten. Dies bedeutet, dass<br />
4,56% <strong>der</strong> Bevölkerung e<strong>in</strong>en IQ von unter 70 o<strong>der</strong> über 130 Punkten haben.<br />
Abweichungen von <strong>der</strong> Normalverteilung<br />
1. Mehrere Gipfel (bimodal bis multimodal)<br />
bedeutet meist, dass die Quelle <strong>der</strong> Variation nicht <strong>zu</strong>fällig ist, z.B. Vokaldauern, wenn Kur<strong>zu</strong>nd<br />
Langvokale <strong>in</strong> e<strong>in</strong>em Datensatz analysiert werden.<br />
60 80 100 120 140 160 180<br />
Vokaldauer [ms]
Modul G.1 WS 06/07: Statistik 15.11.2006 5<br />
2. Asymmetrie (skewness)<br />
Achtung: l<strong>in</strong>kssteil = rechtsschief, rechtsteil = l<strong>in</strong>ksschief<br />
Die Schiefe wird mit dem zentralen Moment dritter Ordnung berechnet. Als zentrales<br />
Moment wird die Differenz e<strong>in</strong>es <strong>in</strong>dividuellen Werts vom Mittelwert bezeichnet:<br />
(x i - x ) a<br />
Der Exponent a bestimmt die Ordnung des zentralen Moments.<br />
a 3 =0: Symmetrie<br />
a 3 0: l<strong>in</strong>kssteil
Modul G.1 WS 06/07: Statistik 15.11.2006 6<br />
3. „Gipfeligkeit“, Exzess, Breite<br />
a 4 =3: normal<br />
a 4 3: leptokurtisch (spitz)
Modul G.1 WS 06/07: Statistik 15.11.2006 7<br />
Rechenbeispiel <strong>zu</strong>r Schiefe <strong>und</strong> Gipfeligkeit e<strong>in</strong>er Verteilung
Modul G.1 WS 06/07: Statistik 15.11.2006 8<br />
Normierung<br />
Wichtig ist, dass die gesamte Fläche unter <strong>der</strong> Kurve gleich 1 ist, also <strong>der</strong> Wahrsche<strong>in</strong>lichkeit<br />
e<strong>in</strong>es fast sicheren Ereignisses entspricht. Somit folgt, dass, wenn zwei gaußsche<br />
Glockenkurven dasselbe μ, aber unterschiedliche σ-Werte haben, jene Kurve mit dem<br />
größeren σ breiter <strong>und</strong> niedriger ist (da ja beide <strong>zu</strong>gehörigen Flächen jeweils den Wert von 1<br />
haben <strong>und</strong> nur die Standardabweichung (o<strong>der</strong> „Streuung“) höher ist). Zwei Glockenkurven<br />
mit dem gleichen σ, aber unterschiedlichen μ haben gleich aussehende Graphen, die jedoch<br />
auf <strong>der</strong> x-Achse um die Differenz <strong>der</strong> μ-Werte <strong>zu</strong>e<strong>in</strong>an<strong>der</strong> verschoben s<strong>in</strong>d.<br />
Standardnormalverteilung <strong>und</strong> die z-Transformation<br />
Die Standardnormalverteilung hat e<strong>in</strong>en Mittelwert von 0 <strong>und</strong> e<strong>in</strong>e Standardabweichung von<br />
1.
Modul G.1 WS 06/07: Statistik 15.11.2006 9<br />
Dichtefunktion <strong>der</strong> Standardnormalverteilung<br />
Eigenschaften <strong>der</strong> z-Verteilung: Die Fläche ist wie<strong>der</strong>um 1 bzw. 100%.<br />
Transformation <strong>zu</strong>r Standardnormalverteilung (z-Transformation)<br />
Ist e<strong>in</strong>e Normalverteilung mit beliebigen μ <strong>und</strong> σ gegeben, so kann diese durch e<strong>in</strong>e<br />
Transformation auf e<strong>in</strong>e<br />
-Normalverteilung <strong>zu</strong>rückgeführt werden.<br />
Die Überführung geschieht durch die z-Transformation <strong>in</strong> die sogenannten z scores.<br />
z i =(x i -x )/s x<br />
Geometrisch betrachtet entspricht die durchgeführte Substition e<strong>in</strong>er flächentreuen<br />
Transformation <strong>der</strong> Glockenkurve von <strong>zu</strong>r Glockenkurve von .<br />
Durch die z-Transformation können sämtliche Normalverteilungen standardisiert werden,<br />
d.h. auf e<strong>in</strong>en Standard gebracht werden. Wir bezeichnen deshalb die Normalverteilung<br />
mit μ= 0 <strong>und</strong> σ=1 als Standardnormalverteilung.
Modul G.1 WS 06/07: Statistik 15.11.2006 10<br />
(vgl. Bortz, 5. Auflage, S. 75, vgl. Übungsaufgabe <strong>zu</strong>r z-Transformation)<br />
Wichtige Anwendung <strong>in</strong> <strong>der</strong> Phonetik: Sprechernormalisierung<br />
Problem: Formanten s<strong>in</strong>d nicht nur von <strong>der</strong> Vokalqualität son<strong>der</strong>n auch von sprecherspezifischen<br />
Merkmalen des Ansatzrohres abhängig.<br />
Lösung:<br />
1. z-Transformation mit sprecherspezifischen <strong>Mittelwerten</strong> <strong>und</strong> Standardabweichungen =<br />
Lobanov-Transformation<br />
F n.norm =(F n -F n.mean )/F n.sd<br />
F n.norm wird für jeden e<strong>in</strong>zelnen Sprecher berechnet.<br />
n entspricht jeweils dem n-ten Formanten (F1, F2 etc.)<br />
2. Daten werden auf den maximalen Range <strong>der</strong> e<strong>in</strong>zelnen Sprecher normalisiert =<br />
Gerstman-Transformation<br />
(vgl. Harr<strong>in</strong>gton & Cassidy (1999) S. 76-78)<br />
F n.norm =(F n -F n.m<strong>in</strong> )/(F n.max -F n.m<strong>in</strong> )