1.3. Ramsey Modell: Bedeutung der Sparquote - CER-ETH

« ≈ 1 of 10 

1.3. Ramsey Modell: Bedeutung der Sparquote 

Theorie (Solow Modell): Sparquote ist eine wichtige fundamentale Größe, die das Niveau des langfristigen 

PKE (Modell ohne technischen Fortschritt) bzw. das Niveau des gleichgewichtigen Wachstumspfades 

des PKE (Modell mit technischem Fortschritt) bestimmt. 

Empirie: Growth Accounting Studien zeigen, dass Kapitalkkumulation (getrieben durch Investitionen 

/ Ersparnisbildung) bedeutsam ist. Darüber hinaus deuten Wachstumsregressionen auf einen 

signifikant positiven Einfluss der Sparquote hin. 

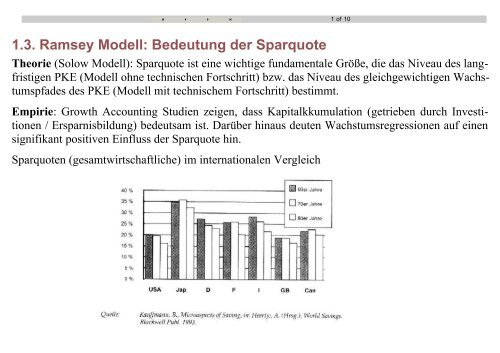
Sparquoten (gesamtwirtschaftliche) im internationalen Vergleich

2 

« ≈ 2 of 10 

1.3. Ramsey Modell: dynamisches Problem der Haushalte (1) 

Annahme: Rationale Haushalte planen ihre Konsum- und Sparentscheidungen vorausschauend 

über mehrere Perioden. Zur analytischen Vereinfachung betrachten wir zunächst ein Zwei-Perioden-Modell. 

Die intertemporale Budgetrestriktion des Haushalts lautet 

C 1 + ÅÅÅÅÅÅÅÅÅÅÅÅÅ 

1 

1 + r C 2 = W 1 + Y L 1 + ÅÅÅÅÅÅÅÅÅÅÅÅÅ 

1 

1 + r Y 2 L (1) 

C 2 = HW 1 + Y L L 

1 - C 1 L H1 + rL + Y 2 (2) 

C 1 : Konsum in der 1. Periode; C 2 : Konsum in der 2. Periode; Y 1 L : Arbeitseinkommen in der 1. Periode; Y 2 L : 

Arbeitseinkommen in der 2. Periode; W 1 : anfängliches Vermögen; r: Zinssatz 

C 2 

3 

2.5 

dC 2 

ÅÅÅÅÅÅÅÅÅÅÅÅ 

dC 1 

=-H1+rL 

2 

1.5 

1 

HW 1 +Y 1 L ,Y 2 L L 

0.5 

0.5 1 1.5 2 2.5 3 

C 1 

©1988-2005 Wolfram Research, Inc. All rights reserved.

« ≈ 3 of 10 


Die intertemporalen Präferenzen des Haushalts seien gegeben durch 

VHC 1 , C 2 L = UHC 1 L + ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ 

1 

(3) 

1 +r UHC 2L 

VHC 1 , C 2 L: intertemporaler Nutzen (Barwert eines Nutzenstroms); UH.L: momentane 

Nutzenfunktion; r ¥ 0: Zeitpräferenzrate 

Zwei wichtige Aspekte 

[1] Die momentane Nutzenfunktion UH.L habe folgende Eigenschaften: U £ H.L > 0 und 

U ≥ H.L < 0. Aufgrund der Konkavität der Nutzenfunktion wünscht der rationale Haushalt 

ein vergleichsweise flaches Konsumprofil {C 1 , C 2 }. 

[2] Sofern r > 0, gewichtet der Haushalt zukünftigen Nutzen UHC 2 L geringer als gegenwärtigen 

Nutzen UHC 1 L. Die Gründe für diese "Gegenwartspräferenz" lauten bspw.: (i) 

generelle Ungeduld und (ii) unsichere Zukunft. 


4 

« ≈ 4 of 10 


Beispiel für eine spezifische, momentane Nutzenfunktion 

U C = C 1-g 

0 b g < 1: konstanter Präferenzparamter 

Die intertemporale Nutzenfunktion V C 1 , C 2 lautet somit 

V C 1 , C 2 = C 1-g 1 + ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ 

1 

1 +r C 1-g 

2 

(4) 

(5) 

3 C2 

2.5 

g=0.9 

2 

1.5 

1 

0.5 

0.5 1 1.5 2 2.5 3 C1 

3 C2 

2.5 

g=0 

2 

1.5 

1 

0.5 

0.5 1 1.5 2 2.5 C1 


« ≈ 5 of 10 

1.3. Ramsey Modell: intertemporales Gleichgewicht (1) 

Das intertemporale Haushaltsoptimum ist durch folgende, notwendige Optimalitätsbedingung 

charakterisiert 

- ∑V . ∑C 1 

ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ =-1 + r 

(6) 

∑V . ∑C 2 

Die Grenzrate der intertemporalen Substitution (linke Seite) muss der Grenzrate 

der intertemporalen Transformation (rechte Seite) entsprechen. 

C 2 

∑V H.Lê∑C 1 

3 

2.5 

2 

1.5 

ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ 

=1+r 

∑V H.Lê∑C 2 

1 

0.5 

0.5 1 1.5 2 2.5 3 

C 1 


6 

« ≈ 6 of 10 

1.3. Ramsey Modell: intertemporales Gleichgewicht (2) 

Unter Verwendung von (5) erhält man 

∑V . 

-g 

ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ = 1 -g C 

∑C 1 

1 

∑V . 

ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ 

1 - g 

∑C 2 1 +r C -g 

2 

Einsetzen in (6) ergibt 

-g 

1 - g C 

ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ 1 

= 1 + r 

H1-gL -g 

ÅÅÅÅÅÅÅÅÅÅÅÅ 

1+r C 2 

-g 

C 

ÅÅÅÅÅÅÅÅÅÅÅÅ 1 

-g 

C = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ 

1 + r 

2 

1 +r 

C 2 

ÅÅÅÅÅÅÅÅ 

C 1 

= 

1 + r ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ 

1 +r 

1 

ÅÅÅÅ 

g 

(7) 

(8) 

(9) 

(10) 

(11) 


« ≈ 7 of 10 

1.3. Ramsey Modell: Keynes-Ramsey-Regel (1) 

Die Wachstumsrate des Konsums kann geschrieben werden als 

C 

ÅÅÅÅÅÅÅÅ 2 

= C 1 +DC 

ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ 

C 1 

C 1 

= 1 + DC ÅÅÅÅÅÅÅÅÅ 

C 1 

= 1 + C` 

Außerdem gilt (Taylor-Approximation der Funktion e x um die Stelle x = 0; siehe bspw. Chiang 

(1984, Kapitel 10.2)) 

(12) 

e x > 1 + x ï x > lnH1 + xL 

Unter Berücksichtigung von (11) und (12) erhält man 

1 + C` = J ÅÅÅÅÅÅÅÅÅÅÅÅÅÅ 

1 + r ÅÅÅÅ 

1 

1 +r N g 

Bildung des natürlichen Logarithmus auf beiden Seiten führt zu 

lnH1 + C` L = ÅÅÅÅÅ 

1 @lnH1 + rL - lnH1 +rLD 

g 

Anwendung von (13) liefert ln 1 + C` 

> C` etc. und somit ergibt sich 

C` > 1 ÅÅÅÅÅ 

g 

Hr -rL 

©1988-2005 

(13) 

(14) 

(15) 

(16) 

Wolfram Research, Inc. All rights reserved.

8 

« ≈ 8 of 10 

1.3. Ramsey Modell: Die Keynes-Ramsey Regel (2) 

Die optimale Wachstumsrate des Konsums ist durch die sog. Keynes-Ramsey-Regel 

gegeben 

C` > 1 ÅÅÅÅÅ 

g r -r 

Ökonomische Interpretation 

(17) 

[1] Die Wachstumsrate des Konsums ist positiv solange r >r. Der Zinssatz r kann als "Prämie" 

interpretiert werden, die ein Haushalt am Kapitalmarkt erhält, wenn er seinen Gegenwartskonsum 

um eine Einheit einschränkt und im Gegenzug den Zukunftskonsum um eine Einheit erhöht. Die 

Zeitpräferenzrate r kann als jene "Prämie" interpretiert werden, die ein Haushalt fordert, damit er 

gerade indifferent bezüglich der Reduktion des Gegenwartskonsums um eine Einheit zugunsten 

einer Steigerung des Zukunftskonsums um eine Einheit ist. Sofern also r >r erscheint es lohnenswert, 

diesen Tausch (intertemporale Konsumsubstitution) einzugehen. 

[2] Die Wachstumsrate des Konsums ist, ceteris paribus, umso höher, je höher der Zinssatz r. Ein 

hoher Zinssatz bedeutet einen hohen Anreiz auf Gegenwartskonsum zu verzichten, um den nichtkonsumierten 

Teil des Einkommens zu sparen, so dass in Zukunft ein höheres Konsumniveau finanziert 

werden kann (r: als Opportunitätskosten des Gegenwartskonsums). 


« ≈ 9 of 10 

1.3. Ramsey Modell: Die Keynes-Ramsey Regel (3) 

Ökonomische Interpretation (fortgesetzt) 

[3] Die Wachstumsrate des Konsums ist umso geringer, je höher die Zeitpräferenzrate r. Eine hohe 

Zeitpräferenzrate bedeutet eine hohe Ungeduld des betrachteten Haushalts. Dies begünstigt den 

Gegenwartskonsum zulasten des Zukunftskonsums. 

[4] Die Wachstumsrate des Konsums ist, ceteris paribus, umso höher, je kleiner der Parameter g 

ausfällt. Ein geringer g-Wert bedeutet gering gekrümmte verlaufende Indifferenzkurven (siehe 

oben) und somit eine hohe Bereitschaft zur intertemporalen Konsumsubstitution. Eine Konstellation 

r -r>0 entfaltet somit starke Anreize, Gegenwartskonsum zugunsten von Zukunftskonsum 

einzuschränken. 

[5] Man beachte, dass es aufgrund von C = cY (mit c: Konsumquote) einen systematischen Zusammenhang 

zwischen der Wachstumsrate des Konsums C` und der Wachstumsrate des Volkseinkommens 

Ỳ gibt. Im einfachsten Fall c = const. gilt: C` = Ỳ. 


10 

« ≈ 10 of 10 

1.3. Ramsey Modell: Zinssatz und makroökonomisches Gleichgewicht 

Die obige Keynes-Ramsey-Regel hat gezeigt, dass dem Zinssatz eine entscheidende Rolle im Hinblick 

auf die Bestimmung der Wachstumsrate des Konsums (mithin des Einkommens) zukommt. Im Solow- 

Modell haben wir bereits gesehen, dass der Zinssatz bei kompetitiven Faktormärkten dem Grenzprodukt 

des Kapitals entspricht. Es bezeichne f HkL die (intensive) Produktionsfunktion und f £ HkL das Grenzprodukt 

des Kapitals. Die Keynes-Ramsey-Regel lautet dann also (bei d =0) 

C` = ÅÅÅÅÅ 

1 

(18) 

g @ f £ HkL -rD 

[1] Diese Form der Keynes-Ramsey-Regel zeigt, dass im makroökonomischen Gleichgewicht alle Faktoren, 

die das Grenzprodukt des Kapitals beeinflussen via Haushaltsentscheidungen auf die Wachstumsrate 

des Konsums durchwirken. 

[2] Für f £ HkL > 0 und f ≥ HkL < 0 (neoklassische Produktionsfunktion) und bei Abwesenheit von technologischem 

Fortschritts sinkt das Grenzprodukt des Kapitals mit steigender Kapitalintensität. Somit wird 

schließlich ein steady state mit C` = 0 erreicht. Dauerhaftes Wachstum ist im Ramsey Modell (wie im 

Solow-Modell) nur bei exogenem technologischen Fortschritt möglich. 

[3] Aus Sicht der Wirtschaftstheorie erscheint eine Maximierung der Wachstumsrate des Volkseinkommens 

weder mikroökonomisch noch makroökonomisch rational. Sofern im Rahmen wirtschaftspolitischer 

Debatten argumentiert wird, eine Steigerung der Wachstumsrate sei wünschenswert, muss zunächst 

ein Marktversagen diagnostiziert werden, das eine suboptimal geringe Wachstumsrate zur Folge hat.

1.3. Ramsey Modell: Bedeutung der Sparquote - CER-ETH

Erfolgreiche ePaper selbst erstellen

Template löschen?

Als Template speichern?