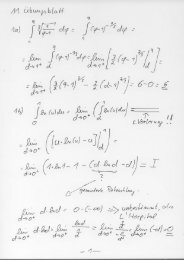Differentialgleichungen

Differentialgleichungen
Zusammenfassung der in der Vorlesung
Mathematische Methoden der Chemie 1 (WS 2012/13)
behandelten Themen
Grundbegriffe und Definition
Unter einer gewöhnlichen Differentialgleichung (=DGL) n-ter Ordnung versteht man eine
Bestimmungsgleichung für eine unbekannte Funktion y=f(x) einer unabhängigen Variablen x,
die Ableitungen dieser Funktion bis zur n-ten Ordnung enthält. Ferner können in der
Gleichung die unbekannte Funktion f(x) sowie die unabhängige Variable x auftreten. Treten
mehrere unabhängige Variable x 1 , x 2 , usw. auf, so heißt die Gleichung partielle DGL.
Eine gewöhnliche DGL n-ter Ordnung heißt linear, wenn
a) die unbekannte Funktion f(x) und alle ihre Ableitungen höchstens in der ersten Potenz
vorkommen, und
b) keine Produkte dieser Größen auftreten.
Allgemeine Form:
( n)
( n−1)
(1)
a ( x)
y + a
−1(
x)
y + ..... + a1(
x)
y + a0(
x)
y = b(
x),
n
n
a ( x)
≠ 0
n
Ist b(x) = 0, so heißt die lineare DGL homogen, ansonsten inhomogen. Tauchen Potenzen
oder Produkte von y (n) = f (n) (x) auf, so heißt die DGL nicht-linear.
Beispiele:
y '(
x)
− 5x
= 0 , linear, 1. Ordnung, gewöhnlich, inhomogen;
y ''(
x)
− 5xy
= 0 , linear, 2. Ordnung, gewöhnlich, homogen
y ( x,
z)
⋅ y'
'(
x,
z)
+ z = 5 + x , nicht-linear, partiell, 2. Ordnung, inhomogen
Die allgemeine Lösung f(x) (=Lösungsschar) einer gewöhnlichen DGL n-ter Ordnung enthält
genau n willkürliche und unabhängige (Integrations-)konstanten. Weist man diesen n
Konstanten in der allgemeinen Lösung einen festen Zahlenwert zu, so erhält man eine
spezielle oder partikuläre Lösung. Gehört eine Lösung keiner Lösungsschar an, so heißt sie
singuläre Lösung.
Beispiel:
2
2
( y ') − 4xy'
+ 4y
= 0 besitzt die Lösungsschar y ( x)
= 2cx
− c , c ∈R, und somit die
partikulären Lösungen y( x)
= 2x
−1,
y(
x)
= 8x
−16,
usw. Aber es existiert auch die
singuläre Lösung
2
y ( x)
= x , welche man nicht aus der Lösungsschar erhalten kann.
Anfangswertproblem:
Um die Integrationskonstanten einer allgemeinen Lösung festzulegen, benötigt man bei einer
DGL n-ter Ordnung in der Regel n weitere Bedingungen. Diese werden im einfachsten Fall
1

durch ein Anfangswertproblem (AWP) vorgegeben. Liegt die DGL als
( n ) , ,
(1) ,..... ( n−
y = f x y y y
1) vor, so bezeichnet man mit einem AWP die Vorgabe der Werte
( )
y .
( n−1)
( x0 ) = y0,
y'
( x0)
= y1,....,
y ( x0)
= yn−
1
Beispiel: Man löse die DGL y '(
x)
= y(
x)
so, dass die Funktion y(x) durch den Punkt P(0,1)
verläuft. Durch Einsetzen kann man zunächst überprüfen, dass die Lösungsschar die Form
x
y ( x)
= Ce besitzt, also eine frei wählbare Konstante C beinhaltet. Diese wird mit dem AWP
0
bestimmt. Es muss gelten 1 = Ce = C , also ist die gesuchte partikuläre Lösung y =
x
( x)
e .
Spezielle Differentialgleichungen 1. Ordnung
Exakte Differentialgleichung
Die DGL
A ( x,
y)
+ B(
x,
y)
⋅ y'(
x)
= 0
heißt exakt, wenn es eine Funktion U(x,y)= constant gibt, so dass
∂U
∂U
U
x
= = A und U
y
= = B
∂x
∂y
gilt. y= y(x) ist im Intervall I genau dann eine Lösung, wenn U(x,y) = const. auf I. Zum
Beweis wird U(x,y) nach x differenziert und man erhält
dU
dx
∂U
∂U
dy
= 0 = + ⋅ = A + By'
= 0 .
∂x
∂y
dx
Man testet auf Exaktheit mit dem Satz von Schwarz; es muss die Integrabilitätsbedingung
∂ A(
x,
y)
∂B(
x,
y
=
)
∂y
∂x
für alle x und y aus dem Definitionsbereich gelten.
Lösungsmethode für die exakte DGL:
Gegeben sei die DGL A ( x,
y)
+ B(
x,
y)
⋅ y'(
x)
= 0 .
1.
∂ A(
x,
y)
∂B(
x,
y
=
) bestätigen .
∂y
∂x
2. Über den Ansatz A = U
x
und B = U
y
eine Stammfunktion U(x,y) bestimmen.
2

a) A unbestimmt nach x integrieren: U ( x,
y)
= ∫ A(
x,
y)
dx + c(
y)
.
b) U partiell nach y ableiten und mit B gleichsetzen:
∂
dc(
y)
U y
( x,
y)
= ( A(
x,
y)
dx) + = B(
x,
y)
∂y
∫
dy
c) c(y) durch Integration nach y bestimmen:
⎡ ∂
⎤
c ( y)
= ∫ ⎢B(
x,
y)
− ( ∫ A(
x,
y)
dx)
⎥dy
⎣ ∂y
⎦
3. Anfangswertproblem (so vorhanden) lösen.
2
Beispiel: y'
( 2y
x ) = −2xy
+ , mit dem AWP y(0)= 1 .
2
Die DGL lässt sich schreiben als 2xy
+ ( 2 y + x ) y'
= 0
A( x,
y)
= 2xy
und
∂A
∂B
1. Exaktheitstest = 2 x,
= 2x
, somit gilt
∂y
∂x
2
2. a) U ( x,
y)
= ∫ 2xydx
+ c(
y)
= x y + c(
y)
∂U
b)
∂y
= x
2
+ c'
( y)
= B(
x,
y)
= 2 y + x
c) c' ( y)
= 2y
, c ( y)
= ∫ 2 ydy = y
2
2
. Somit gilt
B ( x,
y)
+ x
2
= 2y
.
∂A
∂B
= und die DGL ist exakt.
∂y
∂x
. Somit ergibt sich die allgemeine Lösung
2 2
(Lösungsschar) zu U ( x,
y)
= x y + y = const = C .
3. AWP y(0)=1, d.h. 0 2 ⋅1+1 2 =C, C=1. Die gesuchte partikuläre Lösung ist somit
2 2
x y + y = 1 .
Trennbare Differentialgleichungen
Diese haben (evtl. nach Umformung) die Gestalt
dy
y'
= = f ( x)
⋅ g(
y)
dx
mit stetigen und auf den Intervallen x ∈ I und y ∈ J erklärten Funktionen f(x) und g(y) . Der
Lösungsweg ist in diesem Fall besonders einfach und beinhaltet die folgenden Schritte.
1. Sämtliche Nullstellen η von g(y) bestimmen. y(x)=η ist jeweils eine partikuläre
Lösung der DGL.
2. Trennung der Variablen in den Intervallen mit g(y)≠ 0, d.h. auf den verschiedenen
1
Seiten des Gleichheitszeichens steht jeweils nur eine Variable: dy = f ( x)
dx .
g(
y)
dy
3. Jede Seite gemäß G ( y)
= ∫ und F ( x)
=
g(
y)
∫ f ( x)
dx unbestimmt integrieren. Die
allgemeine Lösung lautet dann G ( y)
− F(
x)
= const = C .
4. Falls erforderlich Lösung des AWPs.
3

2 1
Beispiel: y ⋅ y'
= mit dem AWP y(1)=1 , für x gelte x>0 . Umgeschrieben ergibt sich
x
1 1
y'
= 2
y
⋅ x
, d.h. f ( x)
= 1/
x und 2
g ( y)
= 1/ y .
1. g(y) besitzt keine Nullstelle.
2 1
2. Trennung der Variablen ergibt y dy = dx .
x
2 1 3
3. Unbestimmtes Integrieren ergibt G ( y ) =
∫
y dy = y + K1
und
3
1
F ( x)
=
∫
dx = ln( x)
+ K 2 . Die allgemeine Lösung lautet somit 1 y 3 − ln( x)
= C .
x
3
4. Das AWP führt dann zu
1 1
1 3 − ln(1) = C = . Somit lautet die gesuchte partikuläre
3
3
3
3
Lösung y − 3ln( x)
= 1 bzw. explizit y = 3 ⋅ln(
x)
+ 1 .
Diese sind von der allgemeinen Form
Lineare Differentialgleichungen 1. Ordnung
y '(
x)
+ a(
x)
y(
x)
= f ( x)
.
Ist f ( x ) ≠ 0so handelt es sich um eine inhomogene DGL, anderenfalls um eine homogene
DGL. Man muss unbedingt beachten, dass der Faktor vor y’(x) in dieser Darstellung gleich 1
ist, weil nur dann die folgenden Lösungsverfahren angewendet werden können. Die
zugeordnete homogene DGL lautet
y '(
x)
+ a(
x)
y(
x)
= 0 ,
welche durch Trennung der Variablen auf die Form
dy(
x)
dy(
x)
= −a(
x)
y(
x)
⇒ = −a(
x)
dx
dx
y(
x)
gebracht werden kann. Wie bei den trennbaren DGLn beschrieben, kann die zugeordnete
homogene DGL leicht gelöst werden und ergibt
mit der Stammfunktion
− A(
x)
yh ( x)
= c ⋅ e = c ⋅ ~ yh(
x),
c ∈R ,
∫
A ( x)
= a(
x)
dx .
Die allgemeine vollständige Lösung y(x) der inhomogenen DGL ergibt sich aus
y(
x)
=
− A(
x)
yh ( x)
+ y
p(
x)
= c ⋅ e + y
p
( x)
,
4

worin y p (x) eine beliebige partikuläre Lösung der inhomogenen DGL ist. Diese kann man z.
B. durch Raten erhalten, was aber natürlich kein gängiges Verfahren sein kann. Vielmehr
wendet man zur Ermittlung der kompletten Lösung y(x) das Lösungsverfahren Variation der
Konstanten an (=Verfahren von Lagrange). Dazu betrachtet man den Faktor c nicht als
konstant, sondern setzt ihn als Funktion der unabhängigen Variablen x:
Einsetzen in DGL liefert
Somit erhalten wir
y( x)
= c(
x)
⋅ ~ y ( x)
⇒ y'(
x)
= c'(
x)
⋅ ~ y ( x)
+ c(
x)
⋅ ~ y '( x)
.
h
f ( x)
= c'(
x)
⋅ ~ y ( x)
+ c(
x)
⋅ ~ y '( ) + ( ) ⋅ ( ) ⋅ ~
h
x a x c x yh(
x)
h
.
h
= 0!
f ( x)
f ( x)
A(
x)
c'(
x)
= ~ ⇒ c(
x)
= ∫ dx + C = ∫ e f ( x)
dx + C
y ( x)
~
.
y ( x)
h
Die allgemeine Lösung der inhomogen DGL erhält man dann zu
h
A(
x)
− A(
x)
( e f ( x)
dx + C) ⋅ e
y(
x)
= c(
x)
⋅ ~ y ( x)
= ∫ .
h
Wenn nötig, wird zur Bestimmung der Konstanten C das Anfangswertproblem gelöst.
h
1 3
Beispiel 1: y ' + y = x , x,
y > 0 .
x
1. Homogene DGL mit Trennung der Variablen lösen. Es ergibt sich
1 dyh
1 dyh
dx dyh
dx
yh'
+ yh
= 0 ⇒ = − yh
⇒ = − ⇒ = −
x dx x y x
∫
y
∫
x
h
1
⇒ ln( y h ) = −ln(
x)
+ c*
⇒ y h = c ⋅ = c ⋅ y
~
h
x
2. Variation der Konstanten führt zu y( x)
= c(
x)
⋅ ~ y ( x)
. Somit lässt sich c(x) bestimmen
3
f ( x)
x
4 1 5
zu c( x)
= ∫ ~ dx = ∫ dx = ∫ x dx = x + C .
yh(
x)
1
5
x
3. Die gesamte Lösung der inhomogenen DGL ergibt sich dann zu
1 ⎛ 1 5 ⎞ 1 4 C
y( x)
= c(
x)
⋅ ~ yh ( x)
= ⋅ ⎜ x + C ⎟ = x + .
x ⎝ 5 ⎠ 5 x
h
h
Beispiel 2:
y ' = y + x mit dem AWP y ( 0) = 2 .
5

1. Homogene DGL mit Trennung der Variablen lösen. Es ergibt sich
y h
' − y h
= 0 ⇒
dy h dy h
x
= dx ⇒
∫
=
∫
dx ⇒ ln | y h | = x + c*
⇒ y h = c ⋅ e = c ⋅ y
~
h
y h
y h
2. Variation der Konstanten führt zu y( x)
= c(
x)
⋅ ~ y ( x)
. Somit lässt sich c(x) bestimmen
f ( x)
x
( . Dieses Integral lässt sich durch partielle
zu c x)
∫ ~ dx = ∫ dx =
x ∫
− x
= xe dx
yh ( x)
e
− x
Integration lösen und man erhält c(
x)
= −e
( x + 1) + C
3. Die gesamte Lösung der inhomogenen DGL ergibt sich dann zu
− x
x
y( x)
= c(
x)
⋅ ~ y ( x)
= − e ( x + 1) + C ⋅ e = −x
−1
+ C ⋅ e .
h
[ ]
x
0
4. AWP, es sollte sein y(0)=2 . Einsetzen liefert 2 = −1+
C ⋅e
= −1+
C ⇒ C = 3. Somit
x
ergibt sich die gesuchte partikuläre Lösung zu y( x)
= −x
−1
+ 3⋅
e .
h
6