H. Schmidt, FSU - Friedrich-Schiller-Universität Jena
H. Schmidt, FSU - Friedrich-Schiller-Universität Jena
H. Schmidt, FSU - Friedrich-Schiller-Universität Jena
Sie wollen auch ein ePaper? Erhöhen Sie die Reichweite Ihrer Titel.
YUMPU macht aus Druck-PDFs automatisch weboptimierte ePaper, die Google liebt.
Mathematische Biologie 1<br />
- Vorlesungsmitschrift -<br />
Henryk <strong>Schmidt</strong><br />
henryk.schmidt@uni-jena.de<br />
Vortragender<br />
Dr. Gottfried Jetschke<br />
<strong>Friedrich</strong>-<strong>Schiller</strong>-Universität <strong>Jena</strong><br />
Fakultät für Ökologie<br />
28. September 2009
Inhaltsverzeichnis<br />
1 Modelle mit einem Freiheitsgrad 1<br />
1.1 Modelle in stetiger Zeit: Differentialgleichungen . . . . . . . . . . . . . . . . . . . . 2<br />
1.1.1 Grundmodell . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2<br />
1.1.2 Einfache Wachstumsmodelle . . . . . . . . . . . . . . . . . . . . . . . . . . . 3<br />
1.1.3 Logistisch begrenztes Wachstum . . . . . . . . . . . . . . . . . . . . . . . . 4<br />
1.1.4 Inverse Dichteabhängigkeit (Allee-Effekt) . . . . . . . . . . . . . . . . . . 6<br />
1.1.5 Allgemeine Aussagen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7<br />
1.1.6 Beispiele aus Physik und Chemie . . . . . . . . . . . . . . . . . . . . . . . . 8<br />
1.2 Modelle in diskreter Zeit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10<br />
1.2.1 Grundmodell und Beispiele . . . . . . . . . . . . . . . . . . . . . . . . . . . 10<br />
1.2.2 Fixpunkte, Dynamik und Stabilität . . . . . . . . . . . . . . . . . . . . . . . 11<br />
1.2.3 Perioden und Chaos bei der Parabelabbildung . . . . . . . . . . . . . . . . 13<br />
2 Modelle mit zwei Freiheitsgraden 17<br />
2.1 Mathematischer Einschub . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17<br />
2.1.1 Zustandsraum, Trajektorie, Fixpunkt und Stabilität . . . . . . . . . . . . . 17<br />
2.1.2 Stabilitätsanalyse durch Linearisierung . . . . . . . . . . . . . . . . . . . . . 18<br />
2.1.3 Klassifikation von Fixpunkten . . . . . . . . . . . . . . . . . . . . . . . . . . 21<br />
2.2 Modelle zur zwischenartlichen Konkurrenz . . . . . . . . . . . . . . . . . . . . . . . 23<br />
2.2.1 Allgemeines zeitstetiges Modell für Konkurrenz . . . . . . . . . . . . . . . . 23<br />
2.2.2 Spezialfall: Lotka-Volterra-Modell . . . . . . . . . . . . . . . . . . . . . . . . 26<br />
2.3 Modelle zur Prädation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26<br />
2.3.1 Allgemeines Räuber-Beute-Modell . . . . . . . . . . . . . . . . . . . . . . . 26<br />
2.3.2 Modelle ohne Interferrenz . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27<br />
2.3.3 Ergänzungen: Lotka-Volterra-Modelle, Beerntung und Interferenz . . . . . . 29<br />
2.4 Stabile Grenzzyklen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33<br />
2.4.1 Grenzzyklen und Attraktoren . . . . . . . . . . . . . . . . . . . . . . . . . . 33<br />
2.4.2 Ebene Grenzzyklen und Satz von Poincare . . . . . . . . . . . . . . . . . . . 35<br />
2.4.3 Modelle mit Grenzzyklen . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36<br />
2.4.4 Nervenreizleitung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36<br />
2.5 Bifurkationen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37<br />
2.5.1 Elementare Verzweigungs- und Bifurkationstypen . . . . . . . . . . . . . . . 37<br />
2.5.2 Hopf-Bifurkation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41<br />
2.5.3 Globale Bifurkation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42<br />
2.6 Stabilitätsanalysen durch Linearisierung bei Zeitdiskreten Systemen . . . . . . . . 43<br />
3 Modelle mit mehr als zwei Freiheitsgrade 46<br />
3.1 Ein Drei-Trophieebenen Modell . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46<br />
3.2 Invariante Tori . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48<br />
3.3 Chaotische Attraktoren . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49<br />
3.3.1 Beispiele . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49<br />
3.3.2 Allgemeine Eigenschaften chaotischer Attraktoren . . . . . . . . . . . . . . 50<br />
I
Kapitel 1<br />
Modelle mit einem Freiheitsgrad<br />
Bei Modellen mit einem Freiheitsgrad gibt es genau eine Zustandsgröße.<br />
Definition 1 (Extensive Größen).<br />
Extensive Größen sind additiv bei Systemvereinigung. Zum Beispiel Masse, Energie und Stoffmenge<br />
oder auch die Populationsgröße (Anzahl der Individuen, Biomasse).<br />
Definition 2 (Population).<br />
Eine Population umfasst alle Individuen einer Art, die in einem bestimmten Gebiet leben und<br />
interagieren.<br />
Das Ziel dieses Kapitels ist die mathematische Beschreibung der zeitlichen Dynamik der Population.<br />
Dabei werden am Ende<br />
• die ”inneren” Prozesse wie Aufbau und Abbau der Population (Geburt und Sterben)) und<br />
• die Wechselwirkungen mit der Umgebung wie Ein- und Auswanderung<br />
gleichermaßen berücksichtigt.<br />
Es werden folgende Annahmen getroffen:<br />
1. Alle Individuen sind gleich<br />
2. Sehr große Individuenzahlen<br />
3. Population ist räumlich homogen<br />
4. Nur eine Art<br />
Der Zustand zur Zeit t lässt sich durch die Biomasse X(t) ∈ R + beschreiben.<br />
Bemerkung 1.<br />
Weiterhin gelten folgende Zusammenhänge:<br />
1. X(t) ist proportional zur Individuenzahl N(t)<br />
2. Populationsdicht x(t) = X(t)<br />
V<br />
mit V = Fläche bzw. Volumen<br />
3. Zeit t ist entweder stetig (reelle Zahl) oder diskret (natürliche Zahl)<br />
1
Kapitel 1 Modelle mit einem Freiheitsgrad<br />
1.1 Modelle in stetiger Zeit: Differentialgleichungen<br />
1.1.1 Grundmodell<br />
Es gelten zusätzliche Annahmen:<br />
5. Überlappende, nichtsynchrone Generationen → stetige Zeit t ∈ R +<br />
6. Biomassezuwachs ∆x im Zeitzuwachs ∆t sei proportional zu ∆t und abhängig vom aktuellen<br />
Zustand X(t) und der Zeit t, falls ∆t hinreichend klein,<br />
d.h. ∆x = x(t + ∆t) − x(t) = ! f[x(t), t] · ∆t + o(∆t)<br />
f[x(t), t] · ∆t + o(∆t)<br />
lim<br />
∆t→0<br />
→ dx(t)<br />
dt<br />
= f[x(t), t] mit x(t 0 ) = x 0 gegeben<br />
Interpretation:<br />
f(x, t) ist die ”Momentangeschwindigkeit” der Änderung, d.h. ist gleich die Änderungsrate<br />
= absolute Nettoreproduktionsrate mit der Dimension Menge<br />
Zeit<br />
Das Modell ist eindeutig definiert, wenn f(x, t) festgelegt.<br />
Bemerkung 2.<br />
Weitere Spezifizierung:<br />
• Genauere Aufteilung:<br />
f(x, t) = B(x, t)−D(x, t)+I(x, t)−E(x, t) mit B(x, t) absolute Geburtenrate, D(x, t) absolute<br />
Sterberate, I(x, t) absolute Immigrationsrate und E(x, t) absolute Emmigrationsrate<br />
Bei geschlossenen Populationen gilt I = E = 0<br />
• Sinvoll f(x, t) = x · r(x, t) mit r(x, t) spezifische (Pro-Kopf-) Netto-Reproduktionsrate mit<br />
der Dimension Menge<br />
Zeit<br />
Menge = 1<br />
Zeit = 100%<br />
Zeit<br />
Spezialfall: Zeitlich konstante Umwelt<br />
dx(t)<br />
dt<br />
= f(x(t)) mit x(0) = x 0<br />
f : R + → R<br />
(nichtlineare) autonome Differentialgleichung, Abkürzung: dx(t)<br />
dt<br />
= ẋ<br />
Numerische Approximation x(t 0 ) = x 0 gegeben:<br />
x(t 0 + ∆t) ≈ f(x 0 , 0) · ∆t + x 0<br />
x(t 0 + 2 · ∆t) ≈ x(t 0 + ∆t) + f(x(t 0 + ∆t), ∆t) · ∆t<br />
x(t 0 + 3 · ∆t) ≈ · · ·<br />
Euler-Verfahren<br />
2
Kapitel 1 Modelle mit einem Freiheitsgrad<br />
1.1.2 Einfache Wachstumsmodelle<br />
(a) Konstante absolute Geburtenrate ( ˆ= feste Einwanderungsrate)<br />
Modell: ẋ = a mit x(0) = x 0 und a > 0<br />
Lösung: x(t) = x 0 + a · t<br />
Ergebnis:<br />
Lineares Wachstum (bzw. Abnahme für a < 0)<br />
(b) Konstante Pro-Kopf-Geburtenrate ( ˆ=lineare absolute Geburtenrate)<br />
Modell: ẋ = r · x mit x(0) = x 0 und r > 0<br />
Lösung: x(t) = x 0 + a · e rt<br />
Ergebnis:<br />
Exponentielles Wachstum (bzw. Abnahme für e < 0)<br />
3
Kapitel 1 Modelle mit einem Freiheitsgrad<br />
Folge:<br />
konstante Verdopplungszeiten:<br />
Beispiel 1.<br />
x(t + T ) ! = 2 · x(t)<br />
x 0 · e r(t+T ) = 2 · x 0 · e rt<br />
r = 1.4%<br />
a<br />
e rT = 2<br />
rT = ln2<br />
T = ln2<br />
r ≈ 0.69<br />
r<br />
→ T = 70%<br />
1.4%<br />
a<br />
r = 1% a → T = 70%<br />
1%<br />
a<br />
= 50a<br />
= 70a<br />
(c) lineare Pro-Kopf-Geburtenrate ( ˆ=quadratische absolute Geburtenrate)<br />
Modell: ẋ = b · x 2 mit x(0) = x 0 und b > 0<br />
Lösung: x(t) = 1 1<br />
x 0<br />
−bt mit t < t E = 1<br />
bx 0<br />
mit ”Explosion” bei Zeit t E<br />
Ergebnis:<br />
Hyperbolisches Wachstum → Explosion<br />
1.1.3 Logistisch begrenztes Wachstum<br />
bisher: ”freies Wachstum” ẋ = r · x mit x(t) = x 0 · e rt<br />
jetzt: Ressourcen (Nahrung, Raum) sind begrenzt → sollten Wachstum limitieren<br />
4
Kapitel 1 Modelle mit einem Freiheitsgrad<br />
Modellannahme<br />
r = r(x) fallend in x<br />
ˆ= Pro-Kopf-Nettoreproduktionsrate fällt mit wachsender Populationsdichte (r = b − d)<br />
Modell:<br />
ẋ = r(x) · x mit x(0) = x 0 und r(x) fallend in x, r(0) = r max , r(K) = 0<br />
Folge:<br />
Absolute Reproduktionsrate f(x) = r(x) · x durchläuft Maximum:<br />
→ Bei kleinen Dichten x(t) wachsend (x 0 > 0)<br />
→ Bei großen Dichten x(t) fallend<br />
→ Alle Lösungen mit x 0 > 0 erreichen asymptotisch den Wert x ◦ = K<br />
Es existieren zwei Fixpunkte x ◦ (d.h. zwei stationäre Lösungen x(t) ≡ x ◦ )<br />
x ◦ (1) = 0 (instabil) und x◦ (2) = K (stabil)<br />
Spezieller Ansatz: Logistische Differenzialgleichung (Verhulst 1838, Perl/Reed 1920)<br />
(<br />
r(x) = r max · 1 − x )<br />
K<br />
(<br />
→ ẋ = r max · x · 1 − x )<br />
K<br />
Lösung<br />
x(t) = K ·<br />
q +<br />
(<br />
K<br />
x 0<br />
− 1<br />
⎧<br />
1<br />
⎪⎨ K<br />
für t → ∞<br />
) = ≈ x 0 · e<br />
· e −rmaxt ⎪⎩<br />
rmaxt für t klein und x
Kapitel 1 Modelle mit einem Freiheitsgrad<br />
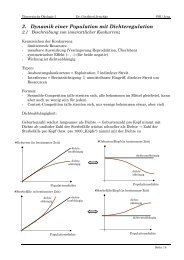
Fazit:<br />
Innerartliche Konkurrenz um begrenzte Ressourcen → dichteabhängige Reproduktion → begrenztes<br />
Wachstum bis zur Kapazität K<br />
1.1.4 Inverse Dichteabhängigkeit (Allee-Effekt)<br />
Falls (bei kleinen Dichten) auch innerartliche Kooperation existiert, dann kommt es zu dem Allee-<br />
Effekt.<br />
→ Modellannahme: r(x) wächst mit Dichte (für kleine Dichten x)<br />
Zwei Fälle:<br />
Unterkritischer Allee-Effekt<br />
Überkritischer Allee-Effekt<br />
f(x) = r(x) · x<br />
Lösung:<br />
Es gilt:<br />
Falls x c < x 0 Erreichen von K<br />
Falls x c > x 0 Abfall auf 0<br />
Fazit:<br />
Im Fall des überkritischen Allee-Effekt existieren drei Fixpunkte:<br />
6
Kapitel 1 Modelle mit einem Freiheitsgrad<br />
• x ◦ (1)<br />
= 0 (Stabiler Fixpunkt)<br />
• x ◦ (2) = x c (Instabiler Fixpunkt, trennt Bereiche in den Annäherung an 0 oder K stattfindet)<br />
• x ◦ (3)<br />
= K (Stabiler Fixpunkt)<br />
→ Bistabilität<br />
Zustandsraum R 1<br />
1.1.5 Allgemeine Aussagen<br />
Autonome Differenzialgleichung ẋ = f(x)) mit x(0) = x 0 und f : R 1 → R 1 bzw. f : Z → R 1<br />
1. Es ist beweisbar, dass f stetig differenzierbar (glatte Funktion)<br />
→ es gibt für alle x 0 eine eindeutige Lösung x(t) auf einem maximalen Intervall (α, β) mit<br />
α < t 0 = 0 < β (β < ∞: ”Explosion”)<br />
2. Geometrisch-Qualitative Aussagen:<br />
f(x 0 ) < 0 → dx ∣<br />
dt t>0<br />
< 0 → x(t) fällt monoton bis zur nächsten Nullstelle x ◦ (oder −∞)<br />
f(x 0 ) > 0 → dx ∣<br />
dt t klein<br />
> 0 → x(t) wächst monoton bis zur nächsten Nullstelle x ◦ (oder ∞)<br />
f(x 0 ) = 0 → x(t) = x 0 → stationäre Lösung<br />
3. Stabilität vom Fixpunkt x ◦<br />
Ein Punkt x ◦ mit f(x ◦ ) = 0 heißt Fixpunkt der Differenzialgleichung.<br />
Zur Stabilität vom Fixpunkt x ◦ : Was passiert bei kleinen Störungen y = x − x ◦ ?<br />
Ein Fixpunkt x ◦ heißt<br />
• stabil, falls alle (kleinen!) Störungen zeitlich klein bleiben<br />
• asymptotisch stabil, falls alle kleineren Störungen auf Null abgebaut werden<br />
• instabil, falls (wenigstens) eine Störung sich aufschaukelt<br />
Kriterium durch Linearisierung:<br />
Sei ẋ = f(x) die Dynamik und x ◦ mit f(x ◦ ) = 0 Fixpunkt.<br />
Setzen y := x − x ◦ → y(t) = x(t) − x ◦ (Zeitlicher Verlauf der Störung)<br />
→ ẏ = ẋ − 0 = f(x) = f(x ◦ + y)<br />
≈ f(x ◦ ) +f ′ (x ◦ ) · y + · · ·<br />
} {{ }<br />
=0<br />
7
Kapitel 1 Modelle mit einem Freiheitsgrad<br />
Näherung:<br />
ẏ = f ′ (x ◦ ) · y → y(t) = y 0 · e λt mit λ = f(x ◦ )<br />
⎧<br />
⎪⎨ ∞ für f ′ (x ◦ ) > 0<br />
→ lim |y(t)| = ≈ |y 0 | für f<br />
t→∞ ⎪⎩<br />
′ (x ◦ ) = 0<br />
0 für f ′ (x ◦ ) < 0<br />
Fazit:<br />
• f ′ (x ◦ ) < 0 → x ◦ asymptotisch stabil<br />
• f ′ (x ◦ ) > 0 → x ◦ asymptotisch instabil<br />
• f ′ (x ◦ ) = 0 → durch Linearisierung keine Aussage möglich (man muss höhere Terme<br />
mitnehmen)<br />
4. Topologische Struktur des Zustandsraums<br />
• Asymptotisch stabile Fixpunkte (= Attraktoren) ziehen alle benachbarten Trajektorien<br />
an<br />
• Die Grenzen der Anziehungsbereiche der Attraktoren sind die (beidseitig) instabilen<br />
Fixpunkte (Repelloren)<br />
(untypischer Grenzfall: ”einseitig instabile Fixpunkte”)<br />
1.1.6 Beispiele aus Physik und Chemie<br />
Physik: Bistabile Federschwinger<br />
entspannte Länge der sei L<br />
tatsächliche Länge sei l = l(x)<br />
→ potentielle Energie V = k 2 · (l − L)<br />
→ Gesamtenergie 2 · k<br />
2 · (l − L)2 = k · (l − L) mit l = √ x 2 + a 2<br />
⇒ V (x) = k · (√ x 2 + a 2 − L ) 2<br />
→ Kraft F (x) = −V ′ (x)<br />
(√ )<br />
= 2k · x2 + a 2 1<br />
− l ·<br />
2 √ x 2 + a · 2x<br />
(<br />
)<br />
2<br />
L<br />
= −2kx · 1 − √<br />
x2 + a<br />
⎛<br />
2 ⎞<br />
= −2kx ⎝1 − L a · 1<br />
√<br />
1 + ( ⎠<br />
)<br />
x 2<br />
a<br />
(<br />
≈ |x|
Kapitel 1 Modelle mit einem Freiheitsgrad<br />
L < a : Federn bei x = 0 am wenigsten gespannt<br />
L > a : Federn bei x = 0 komprimiert<br />
Federn bei x = ±x ◦ gerade gespannt<br />
→ zwei stabile Gleichgewichte<br />
Chemie: bistabile chemische Reaktion - Schlögl<br />
A + 2X −⇀↽−<br />
k1<br />
3X<br />
k2<br />
B + X −⇀↽−<br />
k3<br />
C<br />
k4<br />
Seien Konzentrationen C, A, B konstant und größer gleich Null.<br />
→ Dynamik der Konzentration c X von X (Autokatalyse)<br />
ċ X = −k 3 c B c X + k 4 c C + k 1 c A c 2 X − k 2 c 3 X<br />
”kurz”:<br />
¨c = −x 3 + Ax 2 − Bx + C =: f(x)<br />
f ′ (x) = 3x 2 − 2xA − B ! = 0<br />
x 2 − 2 3 Ax − 2 3 B = 0<br />
x 1,2 reell, falls A 2 > 3B<br />
Bistabil für A 2 > 3B und C 1kr < c < C 2kr<br />
9<br />
x 1,2 = 1 3 ± √<br />
A<br />
2<br />
9 − B 3
Kapitel 1 Modelle mit einem Freiheitsgrad<br />
→ Hysterese<br />
C sehr langsam variiert:<br />
x ◦ stets im ”Quasi-Gleichgewicht”<br />
1.2 Modelle in diskreter Zeit<br />
1.2.1 Grundmodell und Beispiele<br />
Es werden folgende Annahmen getroffen:<br />
1. Alle Individuen sind gleich<br />
2. Sehr große Individuenzahlen<br />
3. Population ist räumlich homogen<br />
4. Nur eine Art<br />
Weiter werden nun folgende Annahmen speziell getroffen:<br />
5. diskrete, synchrone Generationen → diskrete Zeit t ∈ N<br />
6. Populationsgröße x k+1 zur Zeit k + 1 sei abhängig von Populationsgröße x k zur Zeit k<br />
→ Modell:<br />
x k+1 = F (x k ) mit k = 0, 1, 2, ... und x 0 gegeben<br />
F : R 1 → R 1<br />
F : Z → Z 1<br />
Bemerkung 3.<br />
Weitere Zusammenhänge:<br />
1. Ökologie → oft F (x) ! = R(x) · x, d.h. x k+1 = R(x k ) · x k mit R - Nettoreproduktionsfaktor<br />
2. R(x) aus ”mechanistischen” Modell herleitbar, z.b. annuelle Pflanzen<br />
Einfachster Fall: R = konstant<br />
ˆ= freies Wachstum (R > 1) bei unbegrenzten Ressourcen<br />
Lösung:<br />
x n = R n · x 0 mit n = 0, 1, 2, ...<br />
⎧<br />
⎪⎨ ∞ für R > 1<br />
n→∞<br />
−→ x 0 für R = 1<br />
⎪⎩<br />
0 für R < 0<br />
10
Kapitel 1 Modelle mit einem Freiheitsgrad<br />
Modell mit innerartlicher Konkurrenz<br />
Ansatz:<br />
R(x) ≥ 0 und R(x) fallend in x<br />
Typische formelmäßige Ansätze<br />
Bemerkung 4.<br />
R ( x = 1 c<br />
)<br />
= e<br />
−1 · R max ≈ 0.37R max<br />
1<br />
R(x) = R max ·<br />
mit a, b > 0<br />
b<br />
(1 + a · x)<br />
R(x) = R max · e −cx mit c > 0 (Ricker)<br />
mit R max - max. Pro-Kopf-Nettoreproduktionsfaktor<br />
und c Konkurrenzstärke.<br />
Gleichgewichte:<br />
x neu = F (x alt ) ! = x alt<br />
F (x ◦ ) = R(x ◦ ) · x ◦ = x ◦ → x ◦ = 0 oder R(x ◦ ) = 1<br />
1.2.2 Fixpunkte, Dynamik und Stabilität<br />
Modell:<br />
x k+1 = F (x k ) mit k = 0, 1, 2, ... und x 0 gegeben.<br />
F : R 1 → R 1<br />
→ Konstruktion der Dynamik<br />
• numerisch<br />
x 0 gegeben, x 1 = F (x 0 ), x 2 = F (x 1 ) = F (F (x 0 )) , ..., x n = F ((... (F (x 0 )) ...)) = (F n ) (x 0 ) =<br />
(F ◦ F ◦ ... ◦ F ) (x 0 )<br />
11
Kapitel 1 Modelle mit einem Freiheitsgrad<br />
• grafische Konstruktion<br />
x k+1 = F (x k )<br />
• Geometrisch-Qualitativ<br />
Sei x ◦ ein Fixpunkt, d.h. F (x ◦ ) = x ◦ . Wir setzen y = x − x ◦ ”Abweichung”<br />
→ y k+1 = x k+1 − x ◦<br />
= F (x k ) − x ◦<br />
= F (x ◦ + y k ) − x ◦<br />
= F (x ◦ )<br />
} {{ }<br />
x ◦ +F ′ (x ◦ ) · y k + 1 2 · F ′′ (x 0 ) · y 2 k + ... − x ◦ = F ′ (x ◦ ) · y k + ...<br />
Näherung y k+1 = F ′ (x ◦ ) · y k mit k = 0, 1, 2, ... → y n = (F ′ (x ◦ )) n · y 0<br />
⎧<br />
⎪⎨ 0 für |F ′ (x ◦ )| < 1<br />
|y n | = |F ′ (x ◦ ) n | · |y 0 | n→∞<br />
−→ ≡ |y<br />
⎪⎩<br />
◦ | für |F ′ (x ◦ )| = 1<br />
∞ für |F ′ (x ◦ )| > 1<br />
Ergebnis:<br />
Ein Fixpunkt x ◦ der Dynamik x k+1 = F (x k ) ist<br />
(a) asymptotisch stabil falls |F ′ (x ◦ )| < 1<br />
(b) instabil falls |F ′ (x ◦ )| > 1<br />
(c) keine Aussage möglich durch Linearisieren bei |F ′ (x ◦ )| = 1<br />
Vier mögliche Fälle:<br />
12
Kapitel 1 Modelle mit einem Freiheitsgrad<br />
1.2.3 Perioden und Chaos bei der Parabelabbildung<br />
Modell:<br />
Lösung:<br />
x k+1 = r · x k · (1 − x k ) mit k = 0, 1, 2, ... und x 0 gegeben<br />
F (x) = r · x · (1 − x) (Parabelabbildung)<br />
Falls 0 ≤ r ≤ 4, dann wird Zustandsraum [0, 1] nie verlassen!<br />
1. Fixpunkte und Stabilität<br />
F (x ◦ ) = r · x ◦ · (1 − x ◦ ) = x ◦<br />
x ◦ (1) = 0<br />
x ◦ (2) = 1 − 1 r ≥ 0 für r ≥ 1<br />
F ′ (x) = r − 2rx = r · (1 − 2x)<br />
F ′ (0) = r → stabil für r < 1 und instabil für r > 1<br />
(<br />
F ′ 1 − 1 ) (<br />
= r · 1 − 2 + 2 )<br />
= 2 − r<br />
r<br />
r<br />
|2 − r| ! < 1 ↔ −1 < 2 − r < 1<br />
⇒ 1 < r < 3<br />
⇒ x ◦ (2) = 1 − 1 r<br />
stabil für 1 < r < 3 und instabil für 3 < r(≤ 4)<br />
Was bei r > 3?<br />
Periodische Bahnen?<br />
→ z.B. Periode 2:<br />
Es gilt ¯x 1 , ¯x 2 , sodass F (¯x 1 ) = ¯x 2 , F (¯x 2 ) = ¯x 1<br />
⇒ F (F (¯x 2 )) = F (¯x 1 ) = ¯x 2 und F (F (¯x 1 )) = F (¯x 2 ) = ¯x 1<br />
¯x 1 und ¯x 2 sind Fixpunkte von F 2 = F ◦ F , d.h. Lösungen von F (F (x)) = ! x<br />
r · F (x) · (1 − F (x)) = ! x<br />
r · (x · (1 − x) · (1 − (x · (1 − x)))) = x<br />
trivial weil Fixpunkte<br />
{<br />
¯x (1) = 0<br />
¯x (2) = 1 − 1 r<br />
→ Quadratische Gleichung für ¯x (1) , ¯x (2)<br />
¯x (1) , ¯x (2) , ¯x (1) , ¯x (2) , ... stabile Periode 2<br />
↔ ¯x (1) (und ¯x (2) ) stabile Fixpunkte von F 2 (= F ◦ F ), d.h. falls ∣ ∣(F 2 ) ′ (¯x (1) ) ∣ ∣<br />
< 1 und<br />
∣ (F 2 ) ′ (¯x (2) ) ∣ ∣ < 1 gilt:<br />
13
Kapitel 1 Modelle mit einem Freiheitsgrad<br />
Bemerkung 5.<br />
Periode 2 stabil für 3 < r < 3, 4495...<br />
d<br />
dx F (F (¯x) ∣ ∣∣∣¯x1<br />
= F ′ (F (¯x 1 )) · F ′ (¯x 1 )<br />
= F ′ (¯x) · F ′ (¯x 2 )<br />
= d<br />
dx F (F (¯x)) ∣ ∣∣∣¯x2<br />
Was passiert für r > 3, 4495...?<br />
2. Numerische Simulation<br />
x 0 sei beliebig → x 1 , x 2 , ... berechnen<br />
→ x 0 , x 1 , ..., x 1 00 ”transient”<br />
→ x 101 , ..., x 200 ˆ= Attraktor<br />
für 1 < r < r ∞ stabile Perioden 1, 2, 4, 8, ..., 2 n , ... rür r ∞ < r ≤ 4 Attraktoren = Intervalle<br />
aus 1, 2, 4, .., 2 n , ... Stücken<br />
↗ Intervalle periodisch durchlaufen<br />
↘ jede Wiederkehr scheinbar zufällig (irregulär)<br />
→ Chaos<br />
14
Kapitel 1 Modelle mit einem Freiheitsgrad<br />
3. Periodenverdopplung<br />
Geburt einer stabilen Periode 2 durch Heugabelbifurkation:<br />
Weitere Verdoplung:<br />
4. Fenster im Chaos: Intermittenz<br />
Für r ≥ r t3<br />
∼ = 3, 8283 stabile Periode 3<br />
”dann” stabile Periode 6, 12, 24, ...<br />
bei r t3 eine Falten-Bifurkation, in dem Bereich vor r t3 kommt es zu einem Chaos in der<br />
Form von ”Intermittenz” (= scheinbar zufälliger Wechsel von fast periodischen Verhalten<br />
und kurzem irregulären Verhalten), nach r t3 folgt eine stabile Periode 3<br />
≥ r t2·3<br />
→ stabile Periode 6<br />
≥ r t3 und Verdopplung → stabile Periode 6<br />
Fazit:<br />
In jedem beliebig kleinen Intervall von r gibt es periodische Bahnendynamik.<br />
15
Kapitel 1 Modelle mit einem Freiheitsgrad<br />
5. Ljapunow-Experiment<br />
Sei x 0 nur bis auf Genauigkeit ɛ bekannt.<br />
→ n-te Iteration liegt im Intervall der Läge |F n (x 0 + ɛ) − f n (x 0 )| falls ɛ klein<br />
≈ F n (x 0 ) + (F n ) ′ (x 0 ) · ɛ + ...<br />
d.h. Länge ist ≈ |(F n ) ′ (x 0 ) · ɛ|<br />
Vergleich mit der Dynamik z k+1 = ɛ λ · z k mit z n = e (λ)n · z 0<br />
→ dort Spreizung e nλ · ɛ, d.h. e nλ ≈ ! |(F n ) ′ (x)|<br />
Nebenrechnung:<br />
(F n ) ′ (x 0 ) = d<br />
dx F (F n−1 (x))<br />
= F ′ (F n−1 (x 0 )<br />
} {{ }<br />
x n−1<br />
) · (F n−1 ) ′ (x 0 )<br />
= F ′ (x n−1 ) · F ′ (x n−2 ) · · · F ′ (x 1 ) · F ′ (x 0 )<br />
e nλ<br />
≈ ! |(F n ) ′ (x)| = n−1 ∏<br />
k=0<br />
|F ′ (x k )|<br />
1<br />
Setzen λ = λ(x 0 ) := lim<br />
n→∞ n<br />
n−1 ∏ · ln<br />
k=0<br />
|F ′ 1<br />
(x k )| = lim<br />
n→∞<br />
∑<br />
ln |F ′ (x k )|<br />
n · n−1<br />
k=0<br />
λ > 0 ˆ= asymptotisches Entfernen ← Chaos<br />
λ < 0 ˆ= asymptotische Annäherung<br />
↗ Fixpunkte F (x ◦ ) = x ◦ asymptotisch stabil falls |F ′ (x ◦ ) < 1|<br />
→ periodische Bahnen ¯x 1 , ¯x 2 , ..., ¯x N mit F N (¯x i ) = ¯x i<br />
N∏<br />
stabil falls |(F N ) ′ (¯x i )| < 1 bzw. |F ′ (¯x k )| < 1<br />
→ Periodenverdopplung<br />
→ Intermittenz<br />
k=1<br />
(a) x 0 , x 1 , x 2 , ... → stabiler Fixpunkt x ◦<br />
λ = λ(x 0 ) = ln |(F ′ (x 0 ))| ∀x 0 , die zu x ◦ streben<br />
(b) x 0 , x 1 , x 2 , ... → stabile Periode n: T 1 , T 2 , ..., T n<br />
→ λ = λ(x 0 ) = 1 N ·<br />
n∑<br />
ln |F ′ (T i )| < 0 ∀x 0 , die zur Periode streben<br />
i=1<br />
(c) x 0 , x 1 , ... → chaotischer Attraktor A → λ > 0<br />
ˆ= sensitive Abhängigkeit von Anfangswerten<br />
16
Kapitel 2<br />
Modelle mit zwei Freiheitsgraden<br />
2.1 Mathematischer Einschub<br />
2.1.1 Zustandsraum, Trajektorie, Fixpunkt und Stabilität<br />
Wir betrachten nun eine nichtlineare Differnzialgleichung ˙⃗x = ⃗ f (⃗x) mit f i : R n → R 1<br />
ẋ i = dxi<br />
dt<br />
mit i = 1, ..., n<br />
ˆ= n gekoppelte autonome nichtlineare Differenzialgleichungen erster Ordnung.<br />
↗ Integralkurve: Lösung explizit über t<br />
↘ Trajektorie: Lösungskurve im Zustandsraum Z ∈ R n<br />
Fixpunkt von f: F (x ◦ ) ! = 0 → stationäre Lösung:<br />
f i (x ◦ 1, x ◦ 2, ..., x ◦ n) ! = 0 d.h. x(t) ≡ x ◦ für x 0 ≡ x ◦<br />
Wir wissen, f stetig differenzierbar<br />
→ für alle x 0 existiert eine eindeutige Lösung x(t) mit x(0) = x 0 auf Intervall (α, β) mit α < 0 < β<br />
Z.B. → Trajektorien können sich nicht schneiden oder tangieren<br />
↘ Fixpunkt kann nur für t → ±∞ erreicht werden<br />
t ↓ α, t ↑ β ˆ= Rand erreicht<br />
Z = R n , β < ∞ ˆ= Explosion<br />
Existenz einer globalen Lösung (nach vorn, d.h. β = ∞):<br />
M - kompakte Menge<br />
Vektorfeld ρ zeigt stets vom Rand nach Innen<br />
17
Kapitel 2 Modelle mit zwei Freiheitsgraden<br />
x 0 ∈ inneres von M → x(t) existiert für alle t ≥ 0<br />
• Fixpunkt heißt stabil, wenn alle kleinen Störungen klein bleiben<br />
• Fixpunkt heißt asymptotisch stabil, wenn alle kleinen Störungen abgebaut werden<br />
• Fixpunkt heißt instabil, falls wenigstens eine Störung sich aufschaukelt<br />
2.1.2 Stabilitätsanalyse durch Linearisierung<br />
Dynamik:<br />
Fixpunkte:<br />
ẋ i = ⃗ f (⃗x) mit ẋ i = f i (x 1 , x 2 , ..., x n ) und i = 1, ..., n<br />
⃗f ( ⃗x ◦) = 0 ⇔ f i (x ◦ 1, x ◦ 2, ..., x ◦ n)<br />
Wie sieht es nun mit der Stabilität gegenüber kleinen Störungen aus?<br />
”Störung” y := x − x ◦ → Dynamik y(t) = x(t) − x ◦<br />
→ ẏ(t) = ẋ(t) − 0 = f(x)<br />
= f(x ◦ + y) ≈ f(x ◦ ) +f ′ (x ◦ )y + ...<br />
} {{ }<br />
=0<br />
˙⃗y = A(x ◦ )⃗y mit y(0) = y 0 gegeben<br />
A(x ◦ ) = f ′ (x ◦ ) lineare Differenzialgleichung erster Ordnung mit konstanten Koeffizienten<br />
↔ ẏ i = ẋ i = f i (x 1 , ..., x n )<br />
= f i (x ◦ 1 + y 1 , ..., x ◦ n + y n )<br />
= f i (x ◦ 1, x ◦ 2, ..., x ◦ n) + ∑ ∣<br />
∂f i ∣∣∣x=x<br />
· y k<br />
∂x k ◦<br />
(<br />
d.h. Ã(x ◦ ∂fi (x 0 )<br />
) =<br />
∂x k<br />
) n<br />
i,k=1<br />
⇒ Jacobi-Matrix ˆ= Matrix der partiellen Ableitungen<br />
18
Kapitel 2 Modelle mit zwei Freiheitsgraden<br />
Ansatz:<br />
⃗y(t) = ⃗ Y · e λt<br />
( ˆ= Geraden der Trajektorien)<br />
ẏ = ⃗ Y · e λt · λ = Ã(x◦ ) · ⃗Y · e λt<br />
Ã(x ◦ ) ⃗ Y = λ ⃗ Y → λ - Eigenwerte und ⃗ Y - Eigenvektor<br />
Nichttriviale Lösungen ( ⃗ Y ≠ ⃗0) nur für det(A − λI) ! = 0<br />
→ charakteristische Gleichung<br />
λ n + a n (x ◦ )λ n−1 + ... + a n−1 (x ◦ )λ + a n (x ◦ ) ! = 0<br />
→ n Eigenwerte λ 1 , ..., λ n und n Eigenvektoren ⃗ Y (1) , ..., ⃗ Y (n)<br />
→ allgemeine Lösung<br />
→ |y(t)| ≤<br />
n∑<br />
k=1<br />
y(t) =<br />
n∑<br />
c k · ⃗Y (k) · e λ kt<br />
k=1<br />
|c k | · |⃗y| · e λ kt t→∞<br />
−→ 0 falls alle λ k < 0<br />
Bemerkung 6.<br />
λ k kann auch komplex sein → konjugiert komplex.<br />
λ 1,2 = α ± iω<br />
e (α+iω)t = e αt · (cos ωt ± i sin ωt)<br />
→ mit passenden komplexen Koeffizienten entstehen Superkompositionen von e αt cos ωt und e αt sin ωt<br />
Fazit:<br />
• Ein Fixpunkt x ◦ ist asymptotisch stabil, falls Re(λ k ) < 0 ∀ k = 1, 2, ..., n<br />
• Ein Fixpunkt x ◦ ist instabil, falls Re(λ j ) > 0 für wenigstens ein j ∈ {k = 1, 2, ..., n}<br />
Bemerkung 7.<br />
Falls ein Re(λ j ) = 0, dann ist keine Aussage mit Linearisierung möglich.<br />
19
Kapitel 2 Modelle mit zwei Freiheitsgraden<br />
Beispiel 2.<br />
ẋ =u − vx − bxy<br />
ẏ =cxy − dy<br />
Substrat<br />
Konsument<br />
o.B.d.A. sei b = c = 1<br />
ẋ =u − vx − xy mit u, v, d > 0<br />
ẏ =xy − dy<br />
Isoklinen<br />
• ẋ = 0 ⇔ y = u x − v<br />
• ẏ = 0 ⇔ y = 0 oder x = d<br />
Beide Isoklinen zusammen:<br />
Fixpunkt P 1 Fixpunkt P 1<br />
x ◦ (1) = u v und y◦ (1) = 0 x◦ (2) = d und y◦ (2) = u d − v<br />
Jacobi-Matrix:<br />
(<br />
−v − y −x<br />
A(x, y) =<br />
y x − d<br />
)<br />
20
Kapitel 2 Modelle mit zwei Freiheitsgraden<br />
Fixpunkt P 1<br />
→ Charakteristische Gleichung:<br />
( u<br />
) ( )<br />
−v −<br />
u<br />
A<br />
v , 0 =<br />
v<br />
u<br />
0<br />
v − d<br />
0 = ! det<br />
∣ −v − λ<br />
− ∣ u ∣∣∣<br />
v<br />
u<br />
0<br />
v − d − λ<br />
λ 1 = −v < 0<br />
λ 2 = u v − d<br />
λ 2 < 0 falls u v<br />
λ 2 > 0 falls u v<br />
< d → asymptotisch stabiler Knoten<br />
> d → instabiler Sattel<br />
Fixpunkt P 2<br />
→ Charakteristische Gleichung:<br />
A<br />
(d, u ) ( )<br />
−<br />
u<br />
d − v = d<br />
−d<br />
u<br />
d − v 0<br />
0 = ! det<br />
∣ − u d − λ 0<br />
0 −λ ∣<br />
λ 1,2 ...<br />
für u − dv < 0 ↔ u v<br />
für u − dv > 0 ↔ u v<br />
< d → instabiler Sattel<br />
> d → stabiler Strudel oder Knoten<br />
2.1.3 Klassifikation von Fixpunkten<br />
Sei ẏ = Ã(x◦ )⃗y lineare Näherung mit ⃗y ∈ R n und à - (n × n) Matrix<br />
Eine lineare eineindeutige Koordinatentransformation ist<br />
⃗z = ˜Q · ⃗y ↔ ⃗y = ˜Q −1 · ⃗z<br />
→ z(t) = ˜Q · y(t) erfüllt die Differenzialgleichung<br />
ż = ˜Q · ẏ = ˜Q · A · y = Q · A · Q −1 ·z<br />
} {{ }<br />
Matrix<br />
Einfachster Fall:<br />
Eigenwerte reell<br />
⎛<br />
QAQ −1 = ⎜<br />
⎝<br />
⎞<br />
λ 1 0 · · · 0<br />
0 λ 2 · · · 0<br />
.<br />
. . ..<br />
⎟<br />
. ⎠<br />
0 0 · · · λ n<br />
⇔<br />
ż 1 = λ 1 · z 1<br />
ż 2 = λ 2 · z 2<br />
.<br />
ż n = λ n · z n<br />
λit t→∞<br />
→ z i (t) = z i (t) · e −→ 0 falls λ i < 0<br />
in neuen Koordinaten (z) entkoppelte Differenzialgleichungen.<br />
21
Kapitel 2 Modelle mit zwei Freiheitsgraden<br />
Allgemeiner Fall:<br />
Eigenwerte mehrfach komplex<br />
⎛<br />
QAQ −1 =<br />
⎜<br />
⎝<br />
( )<br />
0 · · · 0<br />
( )<br />
0<br />
· · · 0<br />
.<br />
. . ..<br />
( . )<br />
0 0 · · ·<br />
⎞<br />
⎟<br />
⎠<br />
⎛<br />
⇔ d ⎜<br />
dt ⎝<br />
z 1 (t)<br />
z 2 (t)<br />
.<br />
z n (t)<br />
⎛<br />
⎞<br />
⎟<br />
⎠ = ⎜<br />
⎝<br />
( )<br />
0 · · · 0<br />
( )<br />
0<br />
· · · 0<br />
.<br />
. . ..<br />
( . )<br />
0 0 · · ·<br />
⎞<br />
⎛<br />
· ⎜<br />
⎝<br />
⎟<br />
⎠<br />
z 1 (t)<br />
z 2 (t)<br />
.<br />
z n (t)<br />
⎞<br />
⎟<br />
⎠<br />
→ Dynamik wird auf einige niedriger dimensionaler Unterräume reduziert!<br />
Speziell: n = 2<br />
det(A − λI) = 0 ↔ 0 = λ 2 + a 1 (x ◦ )λ + a 2 (x ◦ )<br />
→ λ 1,2 = − a 1<br />
2 ± √<br />
a<br />
2<br />
1<br />
4 − a 2<br />
→ λ 1,2 = α ± iω falls a 2 > a2 1<br />
4<br />
a 1 = 0 → λ 1,2 = −iω → ”Wirbel”<br />
Hurwitz − Kriterium<br />
x ◦ asymptotisch stabil falls a 1 (x ◦ ) > 0 und a 2 (x ◦ ) > 0<br />
x ◦ Strudel falls a 2 (x ◦ ) > a1(x◦ ) 2<br />
4<br />
22
Kapitel 2 Modelle mit zwei Freiheitsgraden<br />
2.2 Modelle zur zwischenartlichen Konkurrenz<br />
Ökologische Annahmen:<br />
1. Bei kleinen Dichten haben beide Arten Wachstum<br />
2. Für beide Arten gibt es inner- und zwischenartliche Konkurrenz<br />
3. Beide Arten besitzen in Monokultur eine Kapazität<br />
4. jede Art kann durch Dominanz der anderen Art am Wachstum gehindert werden<br />
2.2.1 Allgemeines zeitstetiges Modell für Konkurrenz<br />
Mathematisches Modell:<br />
ẋ = x · a(x, y) Population 1<br />
ẏ = y · b(x, y) Population 2<br />
0. a, b stetig differenzierbar<br />
1. a(0, 0) = r 1max > 0, b(0, 0) = r 2max > 0<br />
2. a, b fallend in x und y, d.h. ∂a ∂a<br />
∂x<br />
< 0,<br />
∂y<br />
< 0, ...<br />
3. a(K 1 , 0) = 0, b(0, K 2 ) = 0<br />
4. a(0, N 2 ) = 0, b(K 1 , 0) = 0<br />
mit a(x, y) und b(x, y) Pro-Kopf-Nettoreproduktionsraten.<br />
Mathematische Behandlung<br />
Vektorfeld mit Hauptisoklinen<br />
ẋ = 0 für x = 0 oder auf s := {(x, y)|a(x, y) = 0} = {(x, s(x))|a(x, s(x))) = 0}<br />
ẏ = 0 für y = 0 oder auf w := {(x, y)|b(x, y) = 0} = {(x, w(x))|b(x, w(x))) = 0}<br />
a(x, s(x)) = 0 → da<br />
dx = ∂a<br />
b(x, w(x)) = 0 → db<br />
dx = ∂b<br />
∂x + ∂a<br />
∂y<br />
∂x + ∂b<br />
∂y<br />
∣ · s ′ (x) mit s ′ (x) = ∂a<br />
∂x<br />
∂a < 0 und s(x) streng fallend.<br />
y=s(x) ∂y<br />
∣ · w ′ (x) mit w ′ (x) = ∂b<br />
∂x<br />
< 0 und w(x) streng fallend.<br />
y=w(x)<br />
∂b<br />
∂y<br />
23
Kapitel 2 Modelle mit zwei Freiheitsgraden<br />
Vier mögliche Fälle:<br />
Fall 1: Art 1 gewinnt immer<br />
Fall 2: Art 2 gewinnt immer<br />
Fall 3: Art 1 oder Art 2 gewinnt<br />
Fall 4: Art 1 und Art 2 koexistieren<br />
Fixpunktdiskussion mit Linearisierung<br />
anhand der Jacobi-Matrix<br />
( )<br />
a(x, y) + x · ax x · a<br />
A(x, y) =<br />
y<br />
y · b x b(x, y) + x · b y<br />
A(0, 0) =<br />
A(K 1 , 0) =<br />
A(0, K 2 ) =<br />
mit a x = ∂a<br />
∂x und a y = ∂a<br />
∂y<br />
( a(0, 0) 0<br />
0 b(0, 0)<br />
)<br />
=<br />
( )<br />
r1max 0<br />
0 r 2max<br />
→ λ 1 = r 1max > 0 und λ 2 = r 2max > 0<br />
→ instabiler Knoten<br />
(<br />
K1 · a x K 1 · a y<br />
0 b(K 1 , 0)<br />
λ 1 = K 1 a x < 0<br />
)<br />
λ 2 = b(K 1 , 0) < 0 für N 1 < K 1 und > 0 für N 1 > K 1<br />
→ Stabiler Knoten in Fällen 1 und 3<br />
→ Strudel in Fällen 2 und 4 wenn auch topologisch nicht möglich<br />
( )<br />
a(0, K2 ) 0<br />
K 2 · b x K 2 · b y<br />
λ 2 = K 2 b y < 0<br />
λ 1 = a(0, K 2 ) < 0 für N 2 < K 2 und > 0 für N 2 > K 2<br />
→ Stabiler Knoten in Fällen 2 und 3<br />
→ Instabiler Knoten in Fällen 1 und 4<br />
24
Kapitel 2 Modelle mit zwei Freiheitsgraden<br />
( )<br />
A(x ◦ , y ◦ xax xa<br />
) =<br />
y<br />
yb x yb y 0 = ! det<br />
∣ xa x − λ xa y<br />
yb x yb y − λ ∣<br />
= λ 2 − (xa x + yb y ) · λ + xy · (a x b y − a y b x )<br />
a 1 = −(xa x + yb y ) > 0<br />
a 2 = xy · (a x b y − a y b x ) > 0<br />
↔ a x b y > a y b x<br />
↔ a x<br />
a y<br />
> b x<br />
b y<br />
↔ s ′ (x 0 ) < w ′ (x 0 ) < 0<br />
→ Stabiler Knoten (Fall 4) bzw. Sattel in Fall 3<br />
Bemerkung 8.<br />
Weitere Bemerkungen zu dem Modell:<br />
a 2 − 12 1<br />
4 = x◦ y ◦ · (a x b y − a y b x ) − 1 4 · (x◦ a x + y ◦ b y ) 2 < 0<br />
→ Kein Strudel<br />
1. Auch mehrere innere Fixpunkte möglich<br />
→ stets stabile Knoten oder Sattel (gleiches Kriterium)<br />
→ nur ”Kombinationen” der elementare Fälle<br />
2. globale Existenz der Lösung<br />
jedes Rechteck [o, n] × [0, v] mit u > K 1 und v > K 2 ist invariant<br />
klar:<br />
x = 0, y = 0 Trajektorien<br />
Für x = u < K gilt a(u, 0) < 0 und b(u, 0) < 0<br />
Der Bereich zwischen zwei Isoklinen ist ebenfalls invariant.<br />
3. Modell zeigt Konkurrenz zweier Populationen in zeitlich und räumlich konstanter Umwelt<br />
Drei mögliche Ausgänge:<br />
a) Eine Art gewinnt immer<br />
b) Entweder-Oder-Ausschluss in Abhängigkeit des Anfangwertes (erfordert direkte Konkurrenz<br />
(Interferenz))<br />
c) Coexistenz (Falls N 2 > K 2 ∧ N 1 > K 1 ,<br />
d.h. innerartliche Konkurrenz größer als zwischenartliche Konkurrenz)<br />
4. Zwei sehr ähnliche Arten:<br />
Isoklinen s und w fast parallel<br />
→ Es gewinnt die Art mit der größeren Kapazität<br />
25
Kapitel 2 Modelle mit zwei Freiheitsgraden<br />
2.2.2 Spezialfall: Lotka-Volterra-Modell<br />
Ansatz:<br />
( )<br />
a(x, y) = r 1max · 1 − x+αy<br />
(<br />
K 1<br />
)<br />
b(x, y) = r 2max · 1 − y+βx<br />
K 2<br />
r 1max , r 1max - maximale Pro-Kopf-Nettoreproduktion<br />
α, β - relativen Konkurrenzstärken<br />
N 1 = K2<br />
β , N 2 = K1<br />
α<br />
Koexistenz bei α · β < 1, Ausschluss bei α · β > 1<br />
2.3 Modelle zur Prädation<br />
2.3.1 Allgemeines Räuber-Beute-Modell<br />
Annahmen:<br />
1. Zwei Populationen mit Dichte x(t) für Beute und y(t) für Räuber<br />
2. überlappende, asynchrone Generationen → stetige Zeit<br />
Modellansatz:<br />
Modell der Beute:<br />
Modell der Räuber:<br />
ẋ =<br />
x · r(x)<br />
} {{ }<br />
− y · b(x, y)<br />
} {{ }<br />
innere Dynamik der Beute Mortailität durch Fraß<br />
r(x) - Pro-Kopf-Nettoreproduktionsrate der Beute<br />
→ fallend in x ( ˆ= innerartliche Konkurrenz)<br />
b(x, y) - Pro-Kopf-(der Räuber)-Fressrate der Räuber<br />
→ b(0, y) = 0<br />
→ b(x, y) wachsend in x ˆ= ”funktionelle Reaktion” der Räuber<br />
→ b(x, y) fallend in y ˆ= Interferrenz der Räuber<br />
ẏ = y · c(x, y)<br />
} {{ }<br />
− d(y) · y<br />
} {{ }<br />
Brutto-Zuwachs durch Fraß Mortailität der Räuber<br />
c(x, y) - Pro-Kopf-Bruttozuwachsrate der Räuber<br />
→ c(0, y) = 0<br />
→ b(x, y) wachsend in x ˆ= ”numerische Reaktion”<br />
→ b(x, y) fallend in y<br />
z.b. c(x, y) = u · b(x, y) mit u > 0<br />
d(y) - Pro-Kopf-Mortalität der Räuber<br />
→ d(y) wachsend in y ˆ= Interferrenz<br />
26
2.3.2 Modelle ohne Interferrenz<br />
(1) Grundmodell:<br />
Kapitel 2 Modelle mit zwei Freiheitsgraden<br />
Beute: ẋ = x · r(x) − y · b(x) mit x(0) = x 0 gegeben<br />
Räuber: ẏ = y · c(y) − dy mit y(0) = y 0 gegeben<br />
Bemerkung 9.<br />
r(x) fallend in x und r(K) = 0<br />
→ z.B. r(x) = r max · (1 )<br />
− x K<br />
b(x) wachsend in x und b(0) = 0, meist lim b(x) = b max<br />
( )<br />
x→∞<br />
→ z.B. b(x) = b max ·<br />
x<br />
x+M<br />
c(x) wachsend in x und c(0) = 0, meist c(x) = u · b(x)<br />
(<br />
ẋ = x · r(x) − y · b(x) = x · r(x) − y · b(x) )<br />
x<br />
→ Pro-Kopf-(der Beute)-Mortalität durch Fraß ist y − b(x)<br />
x<br />
(a) b(x) ∼ x → Pro-Kopf-Mortalität durch Fraß konstant<br />
(b) b(x) wächst langsamer als x → Pro-Kopf-Mortalität durch Fraß sinkt<br />
(2) Mathematische Analyse<br />
x 0 = 0 → x(t) ≡ 0 Lösung<br />
ẏ = −dy → y(t) = y 0 · e −dt t→∞<br />
−→ 0<br />
y 0 = 0 → y(t) ≡ 0 Lösung<br />
ẋ = x · r(x) → x(t) t→∞<br />
−→ K<br />
Koordinatenachsen sind Trajektorien! → R 2 t positiv invariant!<br />
Hauptisoklinen<br />
– s-Isokline ẋ = 0<br />
→ y = x·r(x)<br />
b(x)<br />
=: s(x) oder x = 0<br />
s(x)<br />
><br />
=<br />
<<br />
0 für x<br />
<<br />
=<br />
><br />
K<br />
27
Kapitel 2 Modelle mit zwei Freiheitsgraden<br />
s(x) = rmax<br />
b max<br />
· (1<br />
− x K<br />
)<br />
· (x + M) → Parabel mit Nullstelle bei K und −M<br />
→ s(x) wachsend für kleine x falls K > M<br />
– w-Isokline ẏ = 0<br />
↔ y = 0 oder c(x) ! = d ⇔ x = ˆx (falls d < c max )<br />
Fixpunkte:<br />
P 0 = (0, 0)<br />
P 1 = (K, 0)<br />
P 2 = (ˆx, s(ˆx))<br />
Keine Beute und keine Räuber<br />
Keine Räuber, Beute bei K<br />
für s(ˆx) > 0 ⇔ ˆx < K ˆ= Koexistenz von Räuber und Beute<br />
→ Stabilität? → Jacobi-Matrix<br />
( v(x) + x · r<br />
A(x, y) =<br />
′ (x) − y · b ′ (x) −b(x)<br />
y · c ′ (x) c(x) − d<br />
)<br />
A(0, 0) =<br />
(<br />
rmax 0<br />
0 −d<br />
)<br />
A(K, 0) =<br />
→ λ 1 = r max > 0<br />
→ λ 2 = −d < 0<br />
⇒ Sattel<br />
( K · r ′ (K) −b(K)<br />
0 c(K) − d<br />
)<br />
→ λ 1 = K · r ′ (K) < 0<br />
→ λ 2 = c(K) − d<br />
Falls λ 2 > 0 ↔ ˆx < K ⇒ Sattel<br />
Falls λ 2 < 0 ↔ ˆx > K ⇒ Stabiler Knoten<br />
(<br />
ˆx · r<br />
A(ˆx, s(ˆx)) =<br />
′ (ˆx) −b(ˆx)<br />
s(ˆx) · c ′ (ˆx) 0<br />
( s<br />
=<br />
′ (ˆx) · b(ˆx) −b(ˆx)<br />
s(ˆx) · c ′ (ˆx) 0<br />
)<br />
)<br />
28
Kapitel 2 Modelle mit zwei Freiheitsgraden<br />
Eigenwerte bestimmen:<br />
λ 2 −s ′ (ˆx) · b(ˆx) · λ + s(ˆx) · b(ˆx)c ′ (ˆx)<br />
} {{ } } {{ }<br />
a 1<br />
a 2>0 für innere Fixpunkte<br />
Bemerkung 10.<br />
Zu dem Modell:<br />
→ asymptotisch stabil für a 1 (ˆx) = −s ′ (ˆx) · b(ˆx) > 0 ↔ s ′ (ˆx) < 0<br />
→ instabil für s ′ (ˆx) > 0<br />
→ asymptotisches Erreichen eines Grenzzyklus<br />
1. Modell nach MacArthur / Rosenzweig<br />
2. für r(x) = r max · (1 )<br />
− x K , b(x) =<br />
x<br />
x+M · b max und c(x) = u · b(x) alle Terme explizit<br />
berechenbar<br />
ˆx = M ·<br />
d<br />
c max−d = M ·<br />
d<br />
u·b max−d<br />
3. Verhalten mit wachsenden K: Paradoxon der Anreicherung<br />
Zweimal ”transkritische” Verzweigung bei K = 0 und K = ˆx<br />
2.3.3 Ergänzungen: Lotka-Volterra-Modelle, Beerntung und Interferenz<br />
(1) Lotka-Volterra-Modell:<br />
– Einfaches Lotka-Volterra-Modell:<br />
ẋ = ax − bxy<br />
ẏ = cxy − dy<br />
ˆ= Räuber-Beute-Modell mit r(x) ≡ a, b(x) = b · x und c(x))c · x, d.h. keine Kapazitive<br />
Begrenzung, Fraß ist proportional zu x und y und es kommt zu keiner Interferenz.<br />
ẋ = x · (a − by)<br />
ẏ = y · (cx − d)<br />
29
Kapitel 2 Modelle mit zwei Freiheitsgraden<br />
→ ẋ = 0 für x = 0 oder y = a b<br />
→ ẏ = 0 für y = 0 oder x = d c<br />
Fixpunkte:<br />
P 0 = (0, 0)<br />
( d<br />
P 1 =<br />
c , a )<br />
b<br />
Linearisierung bei P 1<br />
→ λ 1,2 = ±iω mit ω = √ ad<br />
→ Zentrum eines Wirbels<br />
ẋ<br />
x<br />
ẏ<br />
· (cx − d) = (a − by) ≡ (a − by) · (cx − d)<br />
y<br />
= cẋ − d · ẋ<br />
x − a · ẏ<br />
y + bẏ ≡ 0<br />
d<br />
(c · x(t) − d · ln x(t) + b · y(t) − a · ln y(t)) ≡ konstant<br />
dt<br />
c · (x(t) − x ◦ · ln x(t)) + b · (y(t) − y ◦ · ln y(t)) ≡ konstant<br />
Anders:<br />
Die Höhenlinien der Funktion H(x, y) = c · (x(t) − x ◦ · ln x(t)) + b · (y(t) − y ◦ · ln y(t))<br />
sind Trajektorien, d.h. H(x(t), y(t)) ≡ H(x 0 , y 0 ) für alle Zeiten t<br />
g z ◦(z) := z − z ◦ ln z ◦<br />
⇒<br />
Trajektorien sind eine Schar geschlossener Bahnen!<br />
30
Kapitel 2 Modelle mit zwei Freiheitsgraden<br />
– Lotka-Volterra-Modell mit Kapazitäten der Beute:<br />
ẋ = x · (a − ex − by) a, b, c, d > 0<br />
ẏ = y · (cx − d − fy) e > 0, f ≥ 0<br />
−ex 2 ˆ= Kapazitive Begrenzung der Beute<br />
−fy 2 ˆ= Interferenz der Räuber ( ˆ=d(y) = d + fy)<br />
f = 0<br />
Räuber stirbt aus<br />
Inneres Gleichgewicht ist stabil<br />
Fazit:<br />
Das Lotka-Volterra-Modell ohne Konkurrenz ist strukturell instabil. (Erklärung<br />
strukturell Instabil siehe Kapitel 2.5)<br />
(2) Funktionelle Reaktion der Räuber<br />
ẋ = x · r(x) − y · b(x)<br />
ẏ = y · c(x) − dy<br />
→ zeigt dauerhafte Oszillationen vom Typ eines Grenzzyklus falls:<br />
– r(x) logistisch begrenzt (= fallend) ist<br />
– b(x) wachsend mit Sättigung (b(x) - Pro-Kopf-(der Räuber)-Fressrate)<br />
z.B. r(x) = r max · (1<br />
− x K<br />
)<br />
und b(x) = bmax ·<br />
x<br />
x+M<br />
Holling-Typen<br />
1. b(x) = ˜b · x<br />
→ zufällig suchende Räuber<br />
31
Kapitel 2 Modelle mit zwei Freiheitsgraden<br />
2. b(x) = x<br />
x+M · b max mit b(M) = 1 2 · b max<br />
→ zufällig suchender Räuber mit Handlingtime<br />
3. b(x) = x2<br />
x 2 +M<br />
· b 2 max mit b(M) = 1 2 · b max<br />
→ zufällig suchender Räuber mit Handlingtime und zusätzlicher beutdichtenabhängiger<br />
Aktivität<br />
(3) Feste Pro-Kopf-Beerntung von Beute und Räuber<br />
M - Halbsättigungskonstante<br />
ẋ = x · r(x) − y · b(x) − ɛ 1 · x<br />
ẏ = y · c(x) − d − ɛ 2<br />
→ höhere Beutedichte<br />
→ geringere Räuberdichte<br />
}<br />
Volterra-Prinzip<br />
(4) Interferenz der Räuber<br />
ẋ = x · r(x) − y · b(x, y) b, c fallend in y<br />
ẏ = y · (c(x, y)) − d(y)) d wachsend in y<br />
Wirkung: Stabilisierend!<br />
32
Kapitel 2 Modelle mit zwei Freiheitsgraden<br />
(5) Variable Beerntung der Räuber<br />
sodass Anzahl der Räuber zeitlich konstant bleibt<br />
ẋ = x · r(x) − y · b(x)<br />
ẏ = y · (r(x) − d) − E(t)<br />
E(t) zeitlich absolute Ernterate der Räuber. Wählen E(t) so, dass dy<br />
dt<br />
E(t) = E(x(t)) = H · (c(x(t)) − d)<br />
z.B. x ˆ= Vegetation, y = H = Herdengröße Pflanzenfresser<br />
Vegetation folgt der Dynamik<br />
ẋ = x · r(x) − H · b(x)<br />
ˆ= dynamisches System mit einem Freiheitsgrad<br />
!<br />
= 0 gilt, d.h. y(t) ≡ H,<br />
→ Gleichgewicht bei x ◦<br />
→ Stationäre Ernte<br />
E ◦ = E(x ◦ (H)) = E(H)<br />
= H(c(x ◦ (H)) − d)<br />
≈ H · c(x(H)) da d ≈ 0<br />
2.4 Stabile Grenzzyklen<br />
2.4.1 Grenzzyklen und Attraktoren<br />
(1) Verhalten für t → ∞<br />
Bisher:<br />
Aber auch möglich:<br />
⃗x(t) → x ◦ (Fixpunkt) oder |⃗x(t)| = ∞<br />
x(t) t→∞<br />
−→<br />
geschlossene Bahn C<br />
Beispiel 3.<br />
ẋ = x − y − x · (x 2 + y 2 )<br />
ẏ = x + y − y · (x 2 + y 2 )<br />
mit x = r · cos ϕ, y = r · sin ϕ<br />
und r = √ x 2 + y 2 , ϕ = arctan y x<br />
33
Kapitel 2 Modelle mit zwei Freiheitsgraden<br />
⇒ ṙ = x2<br />
r<br />
˙ϕ = 1<br />
− xy<br />
r<br />
− x2 r + xy<br />
r<br />
+ y2<br />
r − y2 r = r − r 3<br />
= f(r)<br />
r(t) t→∞<br />
−→ r ◦ = 1 falls r 0 > 0 und ϕ(t) = ϕ 0 + t<br />
→ Stabiler Grenzzyklus!<br />
(2) Begriffe im R n<br />
Definition 3.<br />
Es werden folgende Vereinbarungen getroffen:<br />
(a) Die Menge aller Häufungspunklte einer in x 0 beginnender Trajektorie (für t → ∞) heißt<br />
ω-Grenzmenge (von x 0 )<br />
(b) Eine anziehende und unzerlegbare (= es existiert keine Teilmenge, die allein anziehend<br />
ist) ω-Grenzmenge heißt Attraktor<br />
Beispiel 4.<br />
ẋ = x − x 3<br />
ẏ = −y<br />
34
Kapitel 2 Modelle mit zwei Freiheitsgraden<br />
(c) Ein Grenzzyklus ist eine geschlossene Bahn, die wenigstens eine andere Bahn anzieht.<br />
(d) Ein stabiler Grenzzyklus ist eine geschlossene Bahn, die alle Bahnen aus einer ɛ-Umgebung<br />
anzieht.<br />
Bemerkung 11.<br />
Alle Punkte x 0 , deren Bahnen x(t, x 0 ) den Attraktor A erreichen, heißen Anziehungsbereich<br />
von A.<br />
Typische Situation:<br />
”Fast alle” Punkte des Zustandsraums gehören zum Anziehungsbereich eines Attraktors, eine<br />
”dünne” Restmenge ist ”unentschlossen”.<br />
(3) Spezialfälle n = 1, 2, 3<br />
n = 1<br />
Grenzmengen = Fixpunkte<br />
Attraktoren = asymptotisch stabile Fixpunkte<br />
n = 2<br />
Grenzmengen = Fixpunkte, geschlossene Bahnen + geschlossene Kurven,<br />
die ganz aus Bahnen bestehen<br />
Attraktoren = stabile Fixpunkte und stabilen Grenzzyklen<br />
n = 3<br />
Attraktoren = stabile Fixpunkte, stabilen Grenzzyklen,<br />
stabile invariante Tori und chaotische Attraktoren<br />
2.4.2 Ebene Grenzzyklen und Satz von Poincare<br />
SATZ 2.4.1.<br />
Eine ebene (n = 2), nichtleere, beschränkte und abgeschlossene Grenzmenge, die keinen Fixpunkt<br />
enthält, ist eine geschlossene Kurve.<br />
Korollar 1.<br />
Eine Trajektorie, die in einer beschränkten und abgeschlossenen Menge verbleibt, (ist oder) erreicht<br />
für t → ∞ einen Fixpunkt oder eine geschlossene Bahn.<br />
Kriterien:<br />
(a) Ein ringförmiges Gebiet ohne Fixpunkte, von dessen Rand das Vektorfeld nach innen zeigt,<br />
enthält (wenigstens) einen stabilen Grenzzyklus.<br />
(b) Der innere Rand kann auf einen instabilen Knoten oder Strudel zusammengezogen werrden.<br />
SATZ 2.4.2.<br />
Es gilt:<br />
(a) Im Inneren jeder geschlossenen Bahn gibt es (wenigstens) einen Fixpunkt.<br />
(b) Im Inneren gibt es stets eine ungerade Zahl (2m + 1) Fixpunkte. Davon sind genau m Sattelpunkte.<br />
35
2.4.3 Modelle mit Grenzzyklen<br />
Kapitel 2 Modelle mit zwei Freiheitsgraden<br />
(1) Räuber-Beute Modelle ohne Interferenz<br />
ẋ = x · r(x) − y · b(x)<br />
ẏ = y · (c(x) − d)<br />
(2) Chemische Oszillationen - Brüsselator (Prigogine 1968)<br />
(3) Gestrichene Saite<br />
ẋ = A − (B + 1) · x + x 2 y · b(x)<br />
ẏ = B · x − x 2 y<br />
⇔<br />
m · ẍ = −Kx + F (v) mit F (v) = −βv<br />
ẋ = v<br />
˙v = − K M · x + 1 M · F (v)<br />
⇒ Grenzzykel-Oszillation<br />
(4) Elektrische selbstanregende Schwingungen (Van der Pol / Rayleigh)<br />
ẋ = y<br />
ẏ = ɛ · (1 − x 2 ) · y − x<br />
2.4.4 Nervenreizleitung<br />
Anhand des Fitzhugh-Nagumo-Modell<br />
ẋ = f(x) − y<br />
ẏ = ɛ · (x − γy) · y − x<br />
• s-Isokline ẋ = 0 ⇔ y = f(x)<br />
mit f(x) = −x · (−a + x) · (x − 1)<br />
36
Kapitel 2 Modelle mit zwei Freiheitsgraden<br />
• w-Isokline ẏ = 0 ⇔ y = 1 γ · x<br />
Damit ergeben sich folgende zwei Fälle:<br />
Fall 1 Fall 2<br />
Blockierung hinreichend stark (γ klein)<br />
→ Neuron kann wiederholt feuern<br />
(falls x 0 > a angeregt)<br />
Blockierung ”schwach” (γ groß)<br />
→ Neuron bistabil<br />
Fixpunkte:<br />
Fixpunkt ⇔ f(x) ! = 1 γ · x<br />
→ P 1 = (0, 0) im Fall 1<br />
→ P 1 = (0, 0) und zwei weitere Fixpunkte, bei w ′ > s ′ Fixpunkt stabil<br />
Fixpunkt P 1 = (0, 0) stets stabil!<br />
2.5 Bifurkationen<br />
Betrachten nun Familien von Differenzialgleichungen:<br />
ẋ = f(x, µ)<br />
mit x ∈ R n und Parameter µ ∈ R m<br />
Falls das Trajektorienbild ”in der Nähe” von µ topologisch äquivalent, dann heißt µ regulär, andernfalls<br />
kritisch. Im letzteren Fall heißt das System ẋ = f(x, µ) strukturiell instabil.<br />
2.5.1 Elementare Verzweigungs- und Bifurkationstypen<br />
Fixpunkte<br />
f(x ◦ , µ) = 0 ⇔ F (x ◦ (µ), µ) = 0 ∀µ<br />
→ definiert Lösungszweig(e) x ◦ (µ):<br />
f(x 0 , µ) = ! 0 ˆ= Höhenlinien in f(x, µ) zur Höhe 0<br />
37
Kapitel 2 Modelle mit zwei Freiheitsgraden<br />
[1] Eindimensionaler Zustandsraum (m = 1)<br />
Nur ein Parameter µ (m = 1) → f(x, µ) ist eine ”Fläche”<br />
x ◦ (µ) aus f(x ◦ (µ), µ) = 0 ∀µ bzw.<br />
µ = µ(x ◦ ) aus f(x ◦ , µ(x ◦ )) ≡ 0 ∀x ◦<br />
x ◦ (µ) asymptotisch stabil, falls ∂f(x◦ (µ),µ)<br />
∂x<br />
≡ f x (x ◦ (µ), µ) < 0<br />
→ Stabilitätsgrenze bei f x (x ◦ (µ), µ) ! = 0 → µ = µ c kritischer Parameterwert<br />
Abkürzung x ◦ (µ c ) ≡ x c<br />
d.h. f(x ◦ (µ), µ) ≡ 0 ⇔ f(µ, x ◦ (µ)) ≡ 0<br />
Kritischer Wert zusätzlich f x (x ◦ , µ(x ◦ )) ≡ 0<br />
→ f x (x ◦ , µ(x ◦ )) + f µ (x ◦ , µ(x ◦ )) · µ ′ (x ◦ ) ≡ 0<br />
→ µ ′ (x ◦ ) = −fx<br />
f µ<br />
, falls f µ ≠ 0<br />
speziell µ ′ (x c ) = 0, falls f µ (x ◦ , µ(x ◦ )) ≠ 0<br />
und f xx + 2f xµ · µ ′ (x ◦ ) + f µµ (µ ′ ) 2 + f µ · µ ′′ (x ◦ ) = 0<br />
speziell: µ ′′ (x c ) = − fxx<br />
f µ<br />
(x c , µ c ) ≠ 0, falls f xx (x c , µ c ) ≠ 0<br />
Hieraus resultieren zwei mögliche Fälle:<br />
(1) f µ (x c , µ c ) ≠ 0 → µ ′ (x c ) = 0 → (x c , µ c ) regulärer Umkehrpunkt,<br />
d.h. µ c ist quadratisch nahe (x c , µ c ), tangiert Gerade µ = µ c und f x = −µ ′ (x)f µ<br />
→ f x wechselt in x c Vorzeichen<br />
→ ein Zweig stabil und einer instabil<br />
⇒ Tangenten-Bifurkation / Faltenbifurkation<br />
38
Kapitel 2 Modelle mit zwei Freiheitsgraden<br />
(2) f µ (x c , µ c ) = 0 → (x c , µ c ) singulärer Punkt der Fläche z = f(x, µ) (weil f x = 0, f µ = 0)<br />
ˆ= horizontale Tagentialebene<br />
→ lokales Maximum bzw. Minimum oder Sattel<br />
→ f xx + 2f xµ µ ′ f µµ (µ ′ ) 2 = 0 ↔ f xx (x ′ (µ)) 2 + 2f xµ x ′ (µ) + f µµ = 0<br />
→ quadratische Gleichung für x ′ (µ)<br />
→ x ′ (µ) 1,2 = − fxµ<br />
f xx<br />
±<br />
(2a) f xx (x c , µ c ) ≠ 0<br />
√<br />
fxµ−fµµf xx<br />
f 2 xx<br />
, falls f xx (x c , µ c ) ≠ 0<br />
→ Zwei Lösungen x ′ (µ), falls D := f 2 xµ − f µµ f xx<br />
∣<br />
∣( x c , µ c ) > 0<br />
→ Zwei Lösungszweige x 1,2 (µ), schneiden sich in (x c , µ c )<br />
f x = −f µ · µ ′ (x) = 0 → f x wechselt für jeden Zweig das Vorzeichen<br />
⇒ Transkritische Bifurkation (Stabilitätsaustausch)<br />
(2b) zusätzlich f xx (x c , µ c ) = 0<br />
→ da D = f 2 xµ > 0 muss für f xµ ≠ 0 gelten<br />
→ 2f ′ xµ + f µµ (µ ′ ) 2 = 0 → µ ′ (x c ) = 0 und µ ′ (x c ) = − 2fxµ<br />
f µµ<br />
↔ x ′ (µ c ) = ±∞ und x ′ (µ c ) = − 2fxµ<br />
f µµ<br />
→ µ(x) parabelförmig<br />
≠ ∞ (auch: µ ′′ (x c ) = − fxx<br />
3f xµ<br />
(x c , µ c ) ≠ 0)<br />
Subkritischer Fall<br />
Superkritischer Fall<br />
→ zwei Zweige schneiden sich, einer parabelförmig mit senkrechter Tangente<br />
⇒ Heugabelbifurkation<br />
39
Kapitel 2 Modelle mit zwei Freiheitsgraden<br />
Normalformen<br />
1. Tangentialbifurkation<br />
x ◦ 1,2 = ± √ µ für µ ≥ 0<br />
µ c = x c = 0<br />
ẋ = µ − x 2<br />
2. Transkritische Bifurkation<br />
x ◦ 1 = 0, x ◦ 2 = µ<br />
µ c = x c = 0<br />
ẋ = µx − x 2<br />
3. Heugabelbifurkation<br />
x ◦ 1 = 0, x ◦ 2,3 = ± √ µ für µgeq0<br />
µ c = x c = 0<br />
ẋ = µx − x 3<br />
x ◦ 1 = 0, x ◦ 2,3 = ± √ −µ<br />
µ c = x c = 0<br />
ẋ = −µx + x 3<br />
40
Kapitel 2 Modelle mit zwei Freiheitsgraden<br />
[2] Mehrdimensionaler Zustandsraum (m > 1)<br />
Fixpunkte:<br />
ẋ = f(x, µ)<br />
f(x ◦ , µ) = 0<br />
Linearisierung am Fixpunkt ergibt Eigenwerte λ 1 (µ), ..., λ n (µ)<br />
Einfachster Fall des Verlusts von Stabilität:<br />
λ ( µ c ) = 0, λ i (µ c ) < 0 mit i ≠ k<br />
mit f :<br />
}{{}<br />
R n ×<br />
}{{}<br />
R m → R n<br />
x∈R n µ∈R m<br />
→ in passenden Koordinaten (entlang der Eigenvektoren)<br />
→ Nur in einer (geeigneten) Richtung Änderung der topologischen Eigenschaften der Menge der<br />
Trajektorien<br />
→ in einem passenden Unterraum wieder elementare Bifurkationen<br />
2.5.2 Hopf-Bifurkation<br />
Typisch:<br />
Ein paar konjugiert-komplexe Eigenwerte wechseln das Vorzeichen!<br />
→ für µ < µ c Einspiralen und für µ > µ c Ausspiralen.<br />
Aussage:<br />
Sei x ◦ (µ) Fixpunkt von ẋ = f(x, µ) und seien λ 1 (µ), ..., λ n (µ) die Eigenwerte der Jacobi-Matrix<br />
A(x ◦ (µ)). In der Nähe von µ = µ c gelte λ 1,2 (µ) = α(µ) ± i · ω(µ), λ 3 (µ) < 0, ..., λ n (µ) < 0<br />
Sei α(µ) < 0 für µ < µ c , α(µ c ) = 0 und ω(µ c ) ≠ 0<br />
Falls dα(µ)<br />
d(µ) | µ=µ c<br />
> 0, dann existiert für µ > µ c und µ − µ c hinreichend klein, ein stabiler Grenzzyklus.<br />
Normalform:<br />
ẋ = αx − ωy − x · (ω + cµ + b · (x 2 + y 2 ))<br />
ẏ = ωx + αy<br />
} {{ }<br />
+ y · (dµ − a · (x 2 + y 2 ))<br />
ˆ= ṙ = αr<br />
}<br />
˙ϕ = ω<br />
{{ }<br />
ˆ= ṙ = (dµ − αr 2 ) · r<br />
˙ϕ = ω + rµ + br 2<br />
41
Kapitel 2 Modelle mit zwei Freiheitsgraden<br />
→ für α > 0 subkritische Hopf-Bifurkation√<br />
bei µ c = 0<br />
→ neuer ”Radius” des Grenzzyklus R ◦ dµ<br />
=<br />
a mit Periode T = 2π<br />
ω+µ·(c+ a)<br />
b<br />
Bemerkung 12.<br />
Superkritische Hopf-Bifurkation:<br />
2.5.3 Globale Bifurkation<br />
[1] Kombination lokaler Bifurkationen<br />
z.B. Radius (im Polarkoordinatensystem)<br />
42
Kapitel 2 Modelle mit zwei Freiheitsgraden<br />
[2] Echte globale Verzweigungen<br />
1. Homokline Bifurkation<br />
ˆ= stabiler Grenzzyklus, ”Amplitude” wächst, erreicht Sattel und verschwindet<br />
2. Ω-Explosion<br />
Sattel und Knoten erreichen sich und verschmelzen zu einem Grenzzyklus.<br />
2.6 Stabilitätsanalysen durch Linearisierung bei Zeitdiskreten<br />
Systemen<br />
Wir betrachten:<br />
⃗x neu = ⃗x k+1 = F ⃗ (⃗x k )<br />
x i (k + 1) = F i (x 1 (k), ..., x n (k))<br />
F : R n → R n<br />
k = 0, 1, 2, ... und x 0 gegeben<br />
i = 1, 2, ..., n<br />
(a) Fixpunkte:<br />
x ◦ ! = F (x ◦ )<br />
(b) Stabilität:<br />
y := x − x ◦<br />
y(k) = x(k) − x ◦<br />
→ Dynamik der Abweichungen<br />
y(k + 1) = x(k + 1) − x ◦<br />
= F (x(k)) − x ◦<br />
= F (x ◦ + y(k)) − x ◦<br />
≈ F (x ◦ ) + F ′ (x ◦ ) · y(k) + ... + x ◦<br />
= F ′ (x ◦ ) · y(k) + ...<br />
43
Kapitel 2 Modelle mit zwei Freiheitsgraden<br />
→ Näherung<br />
y(k + 1) = ˜F ′ (x ◦ )<br />
} {{ }<br />
Jacobi-Matrix<br />
·y(k)<br />
Ansatz:<br />
⃗y(k) = ⃗ Y · λ k<br />
→ ⃗y(k + 1) = ⃗ Y · λ k+1<br />
→ ˜F ′ · ⃗Y<br />
! = ˜F ′ · ⃗Y · λ k<br />
!<br />
= λ · ⃗Y ↔ A(x ◦ ) · ⃗Y = λ · ⃗Y<br />
→ n Eigenwerte λ 1 , ..., λ n und n Eigenvektoren ⃗ Y (1) , ..., ⃗ Y (n)<br />
→ Allgemeine Lösung:<br />
∑<br />
⃗y(k) = n c i · ⃗Y (i) · (λ i ) k<br />
i=1<br />
→ ∣y(k)<br />
⃗<br />
∑<br />
∣ ≤ n |c i | · ∣Y ⃗ ( i) ∣ · ∣∣ ∣<br />
λ<br />
k k→∞<br />
i −→ 0 falls alle |λ i | < 1 für i = 1, ..., n<br />
i=1<br />
Ausage:<br />
Der Fixpukt x ◦ der zeitdiskreten Dynamik x(k + 1) = F (x(kl)) ist:<br />
(a) asymptotisch stabil falls |λ i | < 1 ∀i ∈ {1, ..., n}<br />
(b) instabil falls |λ i | > 1 für wenigsten ein j ∈ {1, ..., n}<br />
(c) Falls ein |λ i | = 1 ist keine Aussage möglich<br />
(c) Topologische Typen von Fixpunkten (n = 2)<br />
( )<br />
λ1 0<br />
(a) λ 1 , λ 2 reell, d.h. Ã =<br />
, falls λ<br />
0 λ 1 ≠ λ 2<br />
2<br />
0 < λ 2 < λ 1 < 1<br />
→ stabiler Knoten<br />
−1 < λ 2 < λ 1 < 1<br />
→ stabiler Knoten mit Zick-Zack<br />
44
Kapitel 2 Modelle mit zwei Freiheitsgraden<br />
λ 1 > 1 und/oder λ 2 < −1<br />
→ Sattel<br />
( )<br />
α −ω<br />
(b) λ 1 = λ 2 = α ± iω, d.h. Ã =<br />
ω α<br />
→ Drehung um Winkel ϕ mit ϕ = arctan<br />
√ ω α<br />
α2 + ω 2<br />
und Streckung/Stauchung um Faktor<br />
→ spiralförmige Annäherung/Abstoßung<br />
Fazit:<br />
Topologische Typen analog definierbar, aber größere Vielfalt an Trajektorien, weil Betrag<br />
von λ und Vorzeichen von λ relevant sind. Trajektorien nicht stetig, d.h. ”Sprünge” treten<br />
auf.<br />
45
Kapitel 3<br />
Modelle mit mehr als zwei Freiheitsgrade<br />
3.1 Ein Drei-Trophieebenen Modell<br />
Haben Ressource (R), Pflanze (P ) und Herbivore (H)<br />
Annahmen:<br />
• Abiotische Ressource mit festem absoluten Zustrom I und fester spezifischer Abbaurate q<br />
• Konsumtion (R → P, P → H): Holling-Typ I<br />
• feste spezifische Mortalitäten für P (c) und H(d)<br />
Ressource R allein:<br />
Ṙ = I − qR → Fixpunkt R ◦ = I q<br />
Schreibweise:<br />
Modell:<br />
I := q · ˆR → Fixpunkt R ◦ = ˆR<br />
Ṙ = q( ˆR − R) − a · R · P = q · ˆR − (q + a · P ) · R<br />
P ˙ = a · R · P − b · P · H − c · P = P · (a · R − (b − c) · H)<br />
Ḣ = b · P · H − d · H = H(b · P − d)<br />
Fixpunkte:<br />
H ◦ = 0 oder P ◦ = d b<br />
P ◦ = 0 oder R ◦ = a c<br />
R ◦ = ˆR<br />
P ◦ = q c<br />
( )<br />
ˆR · c<br />
a<br />
> 0<br />
Daraus ergeben sich drei Fixpunkte:<br />
• Fixpunkt F P 1 = ( ˆR, 0, 0)<br />
⇒ Ressource im Gleichgewicht ˆR<br />
( ( ) )<br />
c<br />
• Fixpunkt F P 2 =<br />
a , q c · ˆR<br />
c<br />
a<br />
, 0<br />
→ q · ˆR = ( )<br />
q + ad<br />
b · R<br />
→ R ◦ =<br />
ˆR<br />
1+ a q<br />
d<br />
b<br />
→ H ◦ = aR◦ −c<br />
b<br />
< ˆR<br />
P(2) ◦ ≥ 0 ⇔ ˆR ≥ c a<br />
( (<br />
• Fixpunkt F P 3 = ˆR ·<br />
(<br />
H(3) ◦ > 0 ⇔ R◦ (3) = ˆR ·<br />
1<br />
1+ ad<br />
qb<br />
1<br />
1+ ad<br />
qb<br />
) )<br />
, d b , a·R◦ 3 −c<br />
b<br />
)<br />
≥ c a ⇔ ˆR<br />
(<br />
≥ c a ·<br />
1 + ad<br />
qb<br />
)<br />
> c a<br />
46
Kapitel 3 Modelle mit mehr als zwei Freiheitsgrade<br />
Stabilitätsdiskussion per Jacobi-Matrix<br />
⎛<br />
−(q + aP ) −aR 0<br />
⎞<br />
A(R, P, H) = ⎝ aP aR − c − bH −bP ⎠<br />
0 bH bP − d<br />
Fixpunkt F P 1<br />
A( ˆR, 0, 0) =<br />
⎛<br />
⎝<br />
−q −a ˆR 0<br />
0 a ˆR · c 0<br />
0 0 −d<br />
⎞<br />
⎠<br />
λ 1 = −q < 0<br />
λ 2 = a ˆR − c < 0 ˆR < c a<br />
λ 3 = −d < 0<br />
Fixpunkt F P 2<br />
( c<br />
A<br />
a , q c ·<br />
⎛<br />
(<br />
c<br />
) )<br />
ˆR , 0 =<br />
a<br />
⎝ −q − aP ◦ −c 0<br />
aP ◦ 0 −bP ◦<br />
0 0 bP ◦ − d<br />
⎞<br />
⎠<br />
λ 1 < 0 nach Hurwitz-Kriterium<br />
λ 2 < 0 nach Hurwitz-Kriterium<br />
λ 3 = bP ◦ − d < 0 ⇔ P ◦ < d b ⇔ q (<br />
c · c<br />
)<br />
ˆR<br />
a<br />
< d b ⇔ ˆR < c (<br />
a · 1 + ad )<br />
qb<br />
47
Kapitel 3 Modelle mit mehr als zwei Freiheitsgrade<br />
Fixpunkt F P 3<br />
( ( )<br />
1<br />
A ˆR ·<br />
1 + ad<br />
qb<br />
...<br />
) ⎛<br />
, d b , a · R◦ 3 − c<br />
=<br />
b<br />
⎝ −q − aP ◦ −aR ◦ 0<br />
aP ◦ 0 −bP ◦<br />
0 bH ◦ 0<br />
⎞<br />
⎠<br />
Fazit:<br />
(a) Mit wachsender Nährstoffverfügbarkeit werden immer mehr Trophieebenen (> 0) möglich<br />
(b) Es ist jeweils genau ein lösungszweig stabil (R, R → P, R → P → H)<br />
Bemerkung 13.<br />
Bereich (2) → ˆR bestimmt P ◦<br />
Bereich (3) → ˆR bestimmt H ◦ , P ◦ konstant<br />
3.2 Invariante Tori<br />
Seien ṙ und ż = h(r, z) zwei Differenzialgleichungen, die einen stabilen Grenzzyklus besitzen.<br />
Z.B.<br />
ṙ = A · (B + 1)r + r 2 z<br />
ż = Br − r 2 z B ≥ A 2 + 1<br />
Seien dann ṙ, ż = h(r, z) und ˙ϕ = ω drei Differenzialgleichungen in Zylinderkoordinaten x = r cos ϕ<br />
und y = r sin ϕ<br />
ẋ = ṙ cos ϕ − ṙ sin ϕ · ˙ϕ<br />
= g(r, z) · (√ x<br />
r − g · ) ω<br />
= g x2 + y 2 x<br />
, z · √ − yω<br />
x2 +y 2<br />
= f 1 (x, y, z) (√ )<br />
ẏ = g x2 + y 2 y<br />
, z · √ + yω<br />
x 2 +y 2<br />
= f 2 (x, y, z) (√ )<br />
ż = h x2 + y 2 , z = f 3 (x, y, z)<br />
Grenzzyklus habe Periode T = 2π Ω<br />
, d.h. Kreisfrequenz Ω<br />
(a) ω Ω<br />
rational → Trajektorie schliesst sich zu stabilen Grenzzyklus im ( R3 = m k<br />
Umläufen auf C und m Rotationen um z-Achse<br />
→ Attraktor ist eindimensionale Kurve!<br />
)<br />
ˆ= nach k<br />
(b) ω Ω<br />
irrational → Trajektorie bedeckt einen Torus (der aus der ”Rotation” von C entsteht) dicht.<br />
→ Attraktor ist eine zweidimensionale Fläche!<br />
Bemerkung 14.<br />
In jedem Fall - Fixpunkt, Grenzzyklus, invarianter Torus - ist das Volumen des Attraktors Null!<br />
48
3.3 Chaotische Attraktoren<br />
3.3.1 Beispiele<br />
[1] Populationsdynamik<br />
Kapitel 3 Modelle mit mehr als zwei Freiheitsgrade<br />
Nach Gilpin (1979): Zwei Beuten, ein Räuber und Lotka-Volterra-Dynamik<br />
ẋ = x(1 − x − y − az)<br />
ẏ = y ( 1 − 2 3x − by − z)<br />
ż = z ( a<br />
2 x + 1 2 y − 1) mit a - Präferenz für Beute 1<br />
Fixpunkte:<br />
P 0 (0, ( 0, 0) → instabil, in z-Richtung anziehend<br />
P 1 0,<br />
1<br />
b , 0) = P 1 (0, 1, 0) → nur Beute 2 → instabil<br />
P 2 (1,<br />
(<br />
0, 0) → nur Beute 1, für a > 2 instabil<br />
P 2<br />
)<br />
a−2<br />
3 a<br />
, 0,<br />
a<br />
→<br />
2 )<br />
P 4<br />
(<br />
a−1<br />
N<br />
, a2 −4a+2<br />
N<br />
,<br />
1<br />
2N<br />
→<br />
Verhalten auf Randebenen<br />
nur Beute 1 und Räuber, existiert für a > 2 und für a > 2 + √ 2 instabil<br />
existiert nur für a > 2 + √ 2 und ab ca. a > 5.2 instabil<br />
→ dort stabiler Grenzzyklus ˆ= Hopfbifurkation<br />
mit N := a 2 − 5 2 a + 1<br />
Numerische Integration<br />
→ Periodenverdopplung des Grenzzyklus bei a ≈ 7, a8, 7 und ab a > a ∞ ≈ 10, 5 → chaotische<br />
Bahnen.<br />
Struktur des Attraktors<br />
”Pferdehuf” im Inneren (P 4 ), Ausspiralen erreicht fast den rand, z(t) wird ganz klein, dann Anwachsen<br />
von z, nähert sich den inneren Fixpunkt schräg.<br />
[2] Lorentz-Modell<br />
ẋ = s · (y − x)<br />
ẏ = rx − y − xz<br />
ż = xy − bz<br />
49
Kapitel 3 Modelle mit mehr als zwei Freiheitsgrade<br />
mit s, r, b > 0<br />
(x(t), y(t), z(t)) Lösung → (−x(t), −y(t), −z(t)) ebenfalls Lösung<br />
x 0 = 0, y 0 = 0 → x(t) ≡ 0, y(t) ≡ 0, z(t) = z 0 e −tb → 0<br />
Jede abgeschlossene Kugel K R (m) mit R > 2√ 1 b(s + r) und m = (0, 0, r + s) ist positiv invariant,<br />
weil ⃗v · ⃗f = 1 R · (x · ẋ + y · ẏ + ż · (2 − r − s)) und div f ⃗ = ∂f1<br />
∂x + ∂f2<br />
∂y<br />
+ ∂f3<br />
∂z<br />
= −(s + 1 + b) =<br />
const. < 0<br />
→ Alle V A werden kontrahiert<br />
→ Attraktor von V = 0 wird erreicht<br />
Fixpunkte:<br />
P 0 (0, 0, 0) → immer vorhanden<br />
P 1,2<br />
(± √ b · (r − 1), ± √ )<br />
b · (r − 1), r − 1 → nur für r ≥ 1<br />
Jacobi-Matrix<br />
A(x, y, z) =<br />
⎛<br />
⎝ r − z −1 −x<br />
−s s 0<br />
y x −b<br />
⎞<br />
⎠<br />
A(0, 0, 0) =<br />
⎛<br />
⎝ −s s 0<br />
r −1 0<br />
0 0 −b<br />
λ 3 = −b < 0<br />
a 1 > 0, a 2 > 0 falls 0 ≤ r ≤ 1, a 2 < 0 falls r > 1 → Sattel<br />
⎞<br />
⎠<br />
A(P 1,2 ) = ...<br />
a 1 > 0, a 2 = ..., a 3 > 0 für r > 1<br />
Falls s < b + 1 stabil, falls s > b + 1 dann nur für r < r c = s+b+3<br />
s−b−1 · s stabil, bei r = r c kommt es<br />
zur Hopf-Bifurkation<br />
Bemerkung 15.<br />
Der Lorentz-Attraktor ähnelt einem Schmetterling.<br />
Eindeutige Lösbarkeit → Fläche muss unendlich viele Schichten besitzen.<br />
3.3.2 Allgemeine Eigenschaften chaotischer Attraktoren<br />
(1) Allgemeines<br />
Definition 4 (Chaotischer Attraktor).<br />
Ein chaotischer Attraktor ist ein Attraktor mit sensitiver Abhängigkeit der Bahnen von den Anfangswerten.<br />
Folge:<br />
Trajektorien (höchstens) im Großen periodisch, im Detail irregulär und scheinbar zufällig.<br />
50
Kapitel 3 Modelle mit mehr als zwei Freiheitsgrade<br />
(2) Ljapunow-Exponenten<br />
Gegeben seien zwei Bahnen<br />
ẋ = f(x) mit x(0) = x 0<br />
˙˜x = f(˜x) mit ˜x(0) = ˜x 0 =: x 0 + y 0<br />
→ Abweichung y(t) := ˜x(t) − x(t) genügt der Differenzialgleichung ẏ = ˙˜x − ẋ<br />
Wählen nun:<br />
( n<br />
ẏ = f(˜x) − f(x) = f(x + y) − f(x) ≈ f ′ ∂fi<br />
(x(t) · y(t)) = (x(t)))<br />
∂x j i,j=1<br />
ẏ(t) = A(x(t)) · y(t)<br />
→ y(t + δt) ≈ A(x(t)) · y(t) · δt<br />
(<br />
y (1) (t) = ɛ · (1, 0, 0) → y(t + δt) :≈ ɛ · 1 + ∂f )<br />
1<br />
· δt<br />
∂x 1<br />
(<br />
y (2) (t) = ɛ · (0, 1, 0) → y(t + δt) :≈ ɛ · 1 + ∂f 2<br />
· δt<br />
∂x 2<br />
(<br />
y (3) (t) = ɛ · (0, 0, 1) → y(t + δt) :≈ ɛ · 1 + ∂f 3<br />
· δt<br />
∂x 3<br />
(<br />
)<br />
→ Volumen V (t + δt) ≈ ɛ 3 · 1 + ∂f1<br />
∂x 1<br />
· ∂f2<br />
∂x 2<br />
· ∂f3<br />
∂x 3<br />
· δt<br />
d(V (t)<br />
dt<br />
= V (t) · div ⃗ f mit div ⃗ f := ∂f1<br />
∂x 1<br />
· ∂f2<br />
∂x 2<br />
· ∂f3<br />
∂x 3<br />
)<br />
)<br />
bedeutet: (div f)(x(t)) ist die momentane<br />
(am Punkt x) spezifische Volumenkontraktionsrate, also V (t) ≈ V (0) · e (div f)·t falls t klein, aber<br />
zeitliche Mittelung nötig, da von Punkt x abhängig!<br />
Wir betrachten nun zwei Bahnen mit den Anfangswerten ⃗x 0 , ⃗x 0 + ⃗y 0 .<br />
→ Lösungen ⃗x(t, ⃗x 0 ), ⃗x(t, ⃗x 0 + ⃗y 0 )<br />
Sei weiterhin d 0 := |⃗y 0 | der Anfangsabstand.<br />
→ dann ist der Abstand zur Zeit t: d(t) = |⃗y(t)| = |⃗x(t, ⃗x 0 + ⃗y 0 ) − ⃗x(t, ⃗x 0 )|<br />
Vermutung:<br />
d(t) ≈ d 0 · e λt<br />
genauer: d(x 0 , y 0 , t) ≈ d 0 · e λt für große t und kleine d 0<br />
1 d(x0,y0,t)<br />
→ λ = λ(x 0 , y 0 ) := lim<br />
t→∞ t · ln<br />
d 0<br />
Ljapunow-Exponent λ charakterisiert das Langzeitverhalten infinitesimal benachbart startender<br />
Trajektorien.<br />
Aussage:<br />
Unter schwachen technischen Voraussetzungen gilt:<br />
λ(x 0 , y 0 ) = λ 1 ∀x 0 , (deren Bahnen zur gleichen Grenzmenge führen), die die gleiche Bahn x(t) zur<br />
Grenzmenge M ergeben und ∀y 0 ∈ R n \E n−1 mit E n−1 = n − 1<br />
λ(⃗x 0 , ⃗y 0 ) = λ 2 ≤ λ 1 ∀⃗x 0 , (deren Bahnen zur gleichen Grenzmenge führen), die die gleiche Bahn<br />
x(t) zur Grenzmenge M ergeben und ∀y 0 ∈ E n−1 \E n−2 mit E n−2 = n − 2<br />
.<br />
.<br />
λ(⃗x 0 , ⃗y 0 ) = λ n ≤ λ n−1 ∀⃗x 0 , (deren Bahnen zur gleichen Grenzmenge führen), die die gleiche Bahn<br />
x(t) zur Grenzmenge M ergeben und ∀y 0 ∈ E 1 mit E 1 = 1<br />
51
Kapitel 3 Modelle mit mehr als zwei Freiheitsgrade<br />
Interpretation (R 3 )<br />
Ein kleiner Anfangswürfel der Kantenlänge ɛ 0 verändert Kantenlänge gemäß ɛ 0 · e λ1t , ɛ 0 · e λ2t und<br />
ɛ 0 · e λ3t<br />
→ Volumen V (t) ≈ ɛ 3 0 · e (λ1+λ2λ3)·t = V 0 · e (λ1+λ2+λ3)·t<br />
→ wegen V (t) → 0 muss λ 1 + λ 2 + λ 3 < 0 gelten.<br />
Beispiele (R 3 )<br />
• Asymptotisch stabiler Fixpunkt (−, −, −)<br />
→ λ 1 , 2 , λ 3 = Eigenwerte der Jacobi-Matrix<br />
⇒ 0 > λ 1 > λ 2 > λ 3<br />
• Stabiler Grenzzyklus (0, −, −)<br />
⇒ 0 = λ 1 > λ 2 > λ 3<br />
• Stabiler invarianter Torus (0, 0, −)<br />
⇒ 0 = λ 1 = λ 2 > λ 3<br />
• Chaotischer Attraktor (+, 0, −)<br />
⇒ λ 1 > 0 = λ 2 < λ 3<br />
Definition 5.<br />
Ein Attraktor heißt chaotisch, falls für seine Ljupanow-Exponenten λ 1 ≥ λ 2 ≥ ... ≥ λ n gilt mit<br />
λ 1 > 0<br />
Bemerkung 16.<br />
Dies entspricht dem Mechanismus lokale Expansion + globale Faltung.<br />
52