Abitur 2015; Aufgabe B 1.1

© www.mathe-abi-bw.de Mathe-Abi
Baden-Württemberg
Abitur 2015, Aufgabe B 1.1
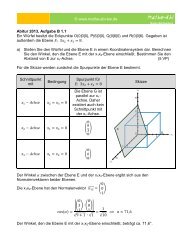
Über einer Terrasse ist als Sonnenschutz
eine Markise an einer Hauswand befestigt.
In einem Koordinatensystem stellen die
Punkte P(0|0|0), Q(5|0|0), R(5|4|0),
S(0|4|0) die Eckpunkte der Terrasse dar.
A
D
Die Markise wird durch das Rechteck mit
den Eckpunkten A(0|0|4), B(5|0|4),
C(5|3,9|2,7), D(0|3,9|2,7) beschrieben
(alle Koordinatenangaben in Meter).
B
P
C
S
Die Lage der Hauswand wird durch die
x 1 x 3 − Ebene beschrieben.
Q
R
a) Bestimmen Sie eine Koordinatengleichung der Ebene, welche die Lage der Markise
beschreibt. Berechnen Sie den Winkel zwischen Markise und Hauswand.
(3 VP)
Eine Parametergleichung der Ebene ergibt sich durch die Punkte A, B und C.
0 5 5
E: x = ( 0) + r ∙ ( 0) + s ∙ ( 3,9 )
4 0 −1,3
Der Normalenvektor dieser Ebene ergibt sich aus dem Kreuzprodukt ihrer
Richtungsvektoren.
5 5 0
0
n⃗ = ( 0) × ( 3,9 ) = ( 6,5 ) oder vereinfacht n⃗⃗⃗⃗ v = ( 1)
0 −1,3 19,5
3
Die Normalengleichung der Ebene lautet daher (z. B. mit Punkt A eingesetzt):
0 0
E: (x − p) ∙ n⃗ = (x − ( 0)) ∙ ( 1) = 0
4 3

© www.mathe-abi-bw.de Mathe-Abi
Baden-Württemberg
Durch Ausmultiplizieren dieser Gleichung ergibt sich die Koordinatengleichung der
Ebene.
E: x 2 + 3x 3 = 12
0
Die x 1 x 3 -Ebene hat den Normalenvektor n⃗⃗⃗⃗⃗⃗ 13 = ( 1)
0
Der Winkel α zwischen Markise und Hauswand berechnet sich aus
0 0
|( 1) ∙ ( 1)|
cos(α) =
3 0
√10 ∙ √1
= 1
√10
⟹ α ≈ 71,6
Der Winkel zwischen Markise und Hauswand beträgt ca. 71,6°.
b) In der Mitte zwischen Q und R steht eine 30cm hohe Stehlampe. Am Markisenrand
CD wird ein senkrecht nach unten hängender Regenschutz angebracht, der genau
bis auf die Terrasse reicht. Bei starkem Wind schwingt er frei um CD.
Kann der Regenschutz dabei die Stehlampe berühren?
Welchen Abstand von der Hauswand darf die Stehlampe auf der Terrasse höchstens
haben, damit dies nicht passiert?
(4 VP)
Der höchste Punkt der Stehlampe ist
L(5|2|0,3).
Die Länge der Regenschutzes ergibt sich aus
der x 3 -Koordinate von Punkt C oder Punkt D.
Er beträgt 2,7m.
A
D
Der Abstand von L und C ergibt sich aus
5 − 5 0
LC ⃗⃗⃗⃗ = OL ⃗⃗⃗⃗⃗ − OC ⃗⃗⃗⃗⃗ = ( 2 − 3,9 ) = ( −1,9)
0,3 − 2,7 −2,4
B
P
C
S
|LC ⃗⃗⃗⃗ | = √1,9 2 + 2,4 2 ≈ 3,06 > 2,7
Q
L
R
Der Abstand zwischen Lampe und Punkt C
beträgt ca. 3,06m. Daher kann der
Regenschutz die Stehlampe nicht berühren.

Der höchste Punkt der Stehlampe ist jetzt L(5|a|0,3).
© www.mathe-abi-bw.de Mathe-Abi
Baden-Württemberg
Der Abstand von L und C ergibt sich aus
5 − 5
0
LC ⃗⃗⃗⃗ = OL ⃗⃗⃗⃗⃗ − OC ⃗⃗⃗⃗⃗ = ( a − 3,9 ) = ( a − 3,9) und |LC ⃗⃗⃗⃗ | = √(a − 3,9) 2 + 2,4 2 > 2,7
0,3 − 2,7 −2,4
Die Terrasse ist 4m breit.
Daher muss der gesuchte
Abstand zwischen 0 und 4
Metern liegen.
Die Lampe darf höchstens
ca. 2,66m von der Wand
entfernt stehen.
c) Die Sonne scheint und der Regenschutz wird entfernt. Die Richtung der
1
Sonnenstrahlen wird durch den Vektor v = ( −1) beschrieben.
−3
Begründen Sie ohne Rechnung, dass die Terrasse nicht vollständig beschattet wird.
Die Markise kann ein- und ausgefahren werden. Dabei bewegen sich die äußeren
Eckpunkte der Markise längs der Geraden BC und AD. Die Markise wird nun so weit
eingefahren, dass der Terrassenrand zwischen Q und R genau zur Hälfte im
Schatten liegt. Bestimmen Sie die neuen Koordinaten der äußeren Eckpunkte der
Markise.
(4 VP)

© www.mathe-abi-bw.de Mathe-Abi
Baden-Württemberg
Die x 2 -Koordinate des Vektors v ist negativ.
Zusätzlich liegt die Vorderkante CD der
Markise nur 3,9m von der Hauswand entfernt,
während die Vorderkante RS der Terrasse 4m
von der Wand entfernt ist.
Daher wird die Terrasse nicht vollständig
beschattet.
B
A
P
C
V
D
S
Q
M
R
Der Schatten reicht jetzt bis zum Punkt M(5|2|0). Der Sonnenstrahl durch den Punkt M
liegt daher auf der Geraden
5 1
g: x = ( 2) + r ( −1)
0 −3
Der Schnittpunkt der Geraden g mit der Markisenebene E: x 2 + 3x 3 = 12 ergibt sich aus
(2 − r) + 3(−3r) = 2 − 10r = 12 ⟹ r = −1
Der Schnittpunkt lautet V(4|3|3) und liegt auf der Vorderkante CD der Markise.
Da der Eckpunkt C* der Markise auf der Kante BC liegt, muss er die x 1 -Koordinate 5
besitzen. Der Punkt lautet daher C*(5|3|3). Dementsprechend liegt der Eckpunkt D* auf
der Kante AD und lautet D*(0|3|3).