Abitur 2014; Aufgabe B 1.1

© www.mathe-abi-bw.de Mathe-Abi
Baden-Württemberg
Abitur 2014, Aufgabe B 1.1
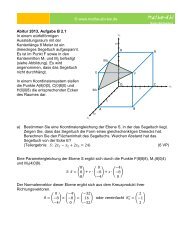
Gegeben sind die Punkte A(5|-5|0), B(5|5|0), C(-5|5|0) und D(-5|-5|0). Das Quadrat ABCD
ist die Grundfläche einer Pyramide mit der Spitze S(0|0|12).
a) Die Seitenfläche BCS liegt in der Ebene E. Bestimmen Sie eine
Koordinatengleichung von E. Berechnen Sie den Winkel, der von der Seitenfläche
BCS und der Grundfläche der Pyramide eingeschlossen wird. Berechnen Sie den
Flächeninhalt des Dreiecks BCS.
(4 VP)
S
10
D
5
R
-5
C
-5
5
Q
A
5
B
Eine Parametergleichung der Ebene ergibt sich durch die Punkte B, C und S.
5 −10 −5
E: x = ( 5) + r ∙ (
0
0
0
) + s ∙ ( −5)
12
Der Normalenvektor dieser Ebene ergibt sich aus dem Kreuzprodukt ihrer
Richtungsvektoren.
−10 −5 0
0
n⃗ = ( 0 ) × ( −5) = ( 120) oder vereinfacht n⃗⃗⃗⃗ v = ( 12)
0 12 50
5

© www.mathe-abi-bw.de Mathe-Abi
Baden-Württemberg
Die Normalengleichung der Ebene lautet daher (Punkt B eingesetzt)
5 0
E: (x − p) ∙ n⃗ = (x − ( 5)) ∙ ( 12) = 0
0 5
Durch Ausmultiplizieren dieser Gleichung ergibt sich die Koordinatengleichung der
Ebene.
E: 12x 2 + 5x 3 = 60
0
Die x 1 x 2 -Ebene hat den Normalenvektor n⃗⃗⃗⃗⃗⃗ 12 = ( 0)
1
Der Winkel α zwischen der Seitenfläche BCS und der Grundfläche ergibt sich aus
0 0
|( 12) ∙ ( 0)|
cos(α) =
5 1
√144 + 25 ∙ √1 = 5
13
⟹ α ≈ 67,4
Der Winkel zwischen der Seitenfläche BCS und der Grundfläche beträgt ca. 67,4°.
Der Flächeninhalt des Dreiecks BCS kann ebenfalls mit dem oben schon verwendeten
Kreuzprodukt berechnet werden.
A BCS = 1 2 |BC ⃗⃗⃗⃗⃗ × BS ⃗⃗⃗⃗⃗ | = 1 −10 −5
2 ∙ |( 0 ) × ( −5)| = 1 0
2 ∙ |( 120)| = 1 2 √1202 + 50 2 = 65
0 12
50
Der Flächeninhalt des Dreiecks BCS beträgt 65 Flächeneinheiten.

© www.mathe-abi-bw.de Mathe-Abi
Baden-Württemberg
b) Betrachtet werden nun Quader, die jeweils vier Eckpunkte auf den Pyramidenkanten
und vier Eckpunkte in der Grundfläche der Pyramide haben. Einer dieser Quader hat
den Eckpunkt Q(2,5|2,5|0). Berechnen Sie sein Volumen. Bei einem anderen dieser
Quader handelt es sich um einen Würfel. Welche Koordinaten hat dessen Eckpunkt
auf der Kante BS?
(4 VP)
Aufgrund der Koordinaten des Eckpunktes Q(2,5|2,5|0) besitzt der Quader eine
quadratische Grundfläche mit einer Länge und Breite von jeweils 5 Längeneinheiten.
Zur Bestimmung der Quaderhöhe dient der Punkt R(2,5|2,5|h), der auf Pyramidenkante
BS liegt.
Die Gerade g durch die Punkte B und S lautet
5 −5
g: x⃗ = ( 5) + r ( −5)
0 12
Durch Gleichsetzten von Gerade g und Punkt R ergibt sich
5 −5 2,5
( 5) + r ( −5) = ( 2,5) ⟹ r = 1 2
0 12 h
und h = 6.
Das Volumen des Quaders beträgt 5 ∙ 5 ∙ 6 VE = 150 Volumeneinheiten
Der Eckpunkt des Würfels ist R W (x 1 |x 2 |x 3 ). Für die seine Koordinaten gilt x 1 = x 2 = 1 x 2
3.
5 −5
Der Eckpunkt liegt ebenfalls auf der Geraden g: x⃗ = ( 5) + r ( −5)
0 12
Daher gilt: 5 − 5r = 1 2
5
∙ 12r ⟹ r = und x 11
3 = 5
60
∙ 12 =
11 11
Der Eckpunkt des Würfels ist R W ( 30
11 | 30
11 | 60
11 ).