Institut für Allgemeine Mechanik der RWTH Aachen

Institut für Allgemeine Mechanik der RWTH Aachen
Prof. Dr.-Ing. D. Weichert 3.Übung
Mechanik II SS 2007 30.04.07
Abgabetermin 3.Übung: 07.05.07 14:00 Uhr
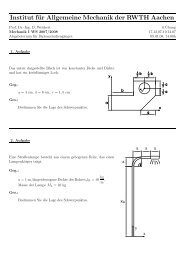
1. Aufgabe
Ein Quader mit dem Übermaß ∆a und dem Untermaß ∆b besteht aus linear-elastischem und homogenem
Material. Er soll in eine rechteckige Aussparung eines starren Körpers eingesetzt werden.
Geg.:
a = 50 mm, b = 30 mm, h = 70 mm,
∆a = 0, 05 mm, ∆b = 0, 002 mm,
E = 2, 1 · 10 5 MPa, α = 12 · 10 −6 K −1 , ν = 0, 3,
σY = 370 MPa.
Ges.: 1. Die Temperaturänderung ∆Θ des Quaders so, dass dieser
gerade in die Nut eingesetzt werden kann.
2. Aufgabe
2. Nach Ausgleich auf Ausgangstemperatur:
(a) Die Spannungen σx, σy und σz sowie die
Längenänderungen ∆a, ∆b und ∆h des Quaders.
(b) Genügt der Spannungszustand im Quader dem
Fließkriterium nach von Mises bzw. nach Tresca?
(c) Bestimmen Sie die Querkontraktionszahl ν für den
Fall, dass das Volumen des Quaders unverändert
bleibt.
Ein zylindrischer Stopfen mit dem Radius R + δ und der Höhe H wird in einen starren Flaschenhals gepresst.
Gegeben: R, δ, H, E, ν.
Gesucht: Bestimmen Sie
1. den Druck p zwischen der Flasche und dem Stopfen,
2. die Höhenänderung ∆H des Stopfens.
H
R +δ
R

Institut für Allgemeine Mechanik der RWTH Aachen
3. Aufgabe
Das dargestellte System besteht aus drei linear-elastischen Stäben mit gleichen Materialeigenschaften. Der Stab 3
ist um δ zu kurz, um im unverformten Zustand sein freies Ende mit dem Gelenk G verbinden zu können.
Geg.:
Ges.:
ℓ, δ (δ ≪ ℓ), A2 = A3 = A, Elastizitätsmodul E.
4. Aufgabe
1. Mit welcher Kraft muss am Stab 3 gezogen
werden, um diesen mit dem Gelenk G zu verbinden?
2. Für den Fall, dass alle drei Stäbe verbunden
sind und die Verschiebung des Gelenkes G in
Richtung des Stabes 3 erfolgt:
(a) Der Querschnitt A1 des Stabes 1.
(b) Die Stabkräfte S1, S2 und S3.
(c) Die Verschiebung u des Gelenkes G.
Das unten dargestellte Fachwerk wird mit einer Kraft � F belastet. Zusätzlich wird der Stab 3 um eine Temperaturdifferenz
∆Θ erwärmt. Die Stäbe bestehen aus dem gleichen Material, haben die Länge ℓ und die Querschnittsfläche
A. Der Wärmeausdehnungskoeffizient α ist gegeben.
Gegeben: F, ℓ, E A, α, β, ∆Θ.
Gesucht: Stellen Sie das zur Bestimmung der Stabkräfte S1, S2 und S3 erforderliche
Gleichungssystem in Matrizenschreibweise auf.
45°
1
F
2
β
3

Institut für Allgemeine Mechanik der RWTH Aachen
Beispielaufgabe
Ein quaderförmiger Gleitstein wird in die Rechtecknut eines starren Körpers eingelegt. Danach wird auf der
Oberseite der Druck p aufgebracht.
Geg.:
Ges.:
b, h, ℓ, p, Elastizitätsmodul E, Querkontraktionszahl ν, Temperaturausdehnungskoeffizient α.
1. Die Spannungen σx, σy und σz im Gleitstein sowie die Längenänderungen ∆h und ∆ℓ.
2. Die Vergleichsspannung σV nach von Mises für ν = 0, 3 und p = 3 · 10 5 Pa.
3. Um wieviel muss der Quader abgekühlt werden, damit er in y-Richtung spannungsfrei wird ?

Beispielaufgabe:
Geg.: b, h, ℓ, p, E, ν, α
1.) Gesucht sind: Spannungen: σx, σy, σz
Allgemeines Hooke’sches Gesetz:
Längenänderungen: ∆h, ∆ℓ
Welche Größen sind im vorhandenen Fall gegeben?
Dehnungen:
εx = ∆ℓ
ℓ
εy = ∆b
b
εz = ∆h
h
εx = 1
E [σx − ν(σy + σz)] (1)
εy = 1
E [σy − ν(σz + σx)] (2)
εz = 1
E [σz − ν(σx + σy)] (3)
= 0 ⇒ Ausdehhnung in y-Richtung nicht möglich wegen der starren
∆h und ∆ℓ sind gesucht.
Spannungen:
Wände, dadurch bauen sich in y-Richtung Spannungen auf. Dies
nennt man behinderte Kontraktion.
σx = 0 ⇒ keine Behinderung, keine Last
σy =? ⇒ gesucht, s. εy
σz =? ⇒ berechenbar, Gleitstein schneiden

x
z
l
y
p
s z
b
Kräftegleichgewicht in z-Richtung:
−p ℓ b − σz ℓ b = 0
σz = −p (Druckspannung)
nun σz = −p, εy = 0, σx = 0 in Gleichungen (1) bis (3) einsetzen:
aus(5): σy = −ν p
aus(4): εx = − ν
(−ν p − p)
E
∆ℓ
ℓ
ν
= p (ν + 1)
E
∆ℓ = ν
p ℓ (ν + 1)
E
aus(6): εz = 1
[−p − ν (−ν p)]
E
∆h
h
= 1
E p (ν2 − 1)
∆h = 1
E p h (ν2 − 1)
(1) ⇒ εx = 1
E [0 − ν(σy − p)]
εx = − ν
E (σy − p) (4)
(2) ⇒ 0 = 1
E [σy − ν(−p + 0)]
0 = 1
E (σy + νp) (5)
(3) ⇒ εz = 1
[−p − ν(0 + σy)]
E
εz = 1
E (−p − νσy) (6)

2.) Gesucht ist: Vergleichsspannung nach von Mises mit ν = 0, 3 und p = 3 · 10 5 Pa
Idee der Vergleichsspannung
Spannungen des mehrachsigen Spannungszustandes auf gleichwertige einachsige Ver-
gleichsspannung σV zurückführen. σV kann dann mit den Kennwerten aus dem ein-
achsigen Zugversuch verglichen werden.
σV < σF: elastisches Materialverhalten
σF (Fließspanung) �=σY (Yieldstress, to yield: fließen)
σV = σF: plastisches Materialverhalten
(bei uns: linear-elastisch, ideal-plastisches Material)
Fließbedingung nach v. Mises:
Es gilt:
Auch hier ist die Beurteilung eines mehrdimensionalen Spannungszustandes schwie-
rig bezüglich der plastischen Verformung des Materials. Daher wird eine skalare
Größe F eingeführt, um den Zustand des Materials zu beurteilen.
Komponentenschreibweise:
F = 1
6 [(σx − σy) 2 + (σy − σz) 2 + (σz − σx) 2 ] + τ 2 xy + τ 2 yz + τ 2 xz − 1
3 σ2 Y
nach σY aufgelöst:
σY =
� 1
2 [(σx − σy) 2 + (σy − σz) 2 + (σz − σx) 2 ] + 3[τ 2 xy + τ2 yz + τ2 xz ]
� �� �
≡ σv
⇒ F ∗ = σV − σY = 0
mit:
σx, σy, σz
τxy, τyz, τxz
σV : Vergleichsspannung
σY �= σF: Fließspannung
�
auftretende Spannungen
= 0

Für dieses Beispiel:
σx = 0; τxy = τyz = τxz = 0 keine Schubspannung
�
�
⇒ σV =
�
� 1
[( σx
2
����
=0
σV = � σ 2 y − σyσz + σ 2 z
mit: σy = −ν p und σz = −p
σV = p √ ν 2 − ν + 1
−σy) 2 + (σy − σz) 2 + (σz − σx
mit: ν = 0, 3 und p = 3 · 10 5 Pa
σV = 3 · 10 5 Pa � 0, 3 2 − 0, 3 + 1
σV = 2, 67 · 10 5 Pa = 0, 267 N
mm 2
����
=0
3.) Ges.: ∆Θ (Temperaturdifferenz) damit σy = 0
Es galt ohnehin: εy = 0, σx = 0, σz = −p
Gl.(4.35) Umdruck (mechanische und thermische Dehnung)
εy = 1
E [σy − ν (σz + σx)] + α ∆Θ
0 = 1
[0 − ν (0 − p)] + α ∆Θ
E
0 = 1
ν p + α ∆Θ
E
ν p
∆Θ = −
E α
) 2 ] + 3[τ 2 xy + τ2 yz + τ2 xz ]
� �� �
=0

Institut für Allgemeine Mechanik der RWTH Aachen
Lösungshilfen für 3. Übung Mechanik II SS 2007:
1. Aufgabe
1.) ∆θ = −83, 25 K
2.a) σx = −225, 92 N
mm 2 σy = −53, 78 N
mm 2 σz = 0
∆ā = −∆a = −0, 05 mm ∆ ¯ b = ∆b = 0, 002 mm ∆h = 0, 028 mm
2.b) v. Mises: F(σij) = −31705 N2
mm 4
2.c) ν = 1/2
Tresca: F(σij) = −72, 04 N
mm 2
2. Aufgabe
δ E
1.) p =
(R + δ) (1 − ν)
2.) ∆H =
3. Aufgabe
1.) S3 =
δ E A
√ 5ℓ
2.) (a) A1 = 1
2 A
2 δ ν H
(R + δ) (1 − ν)
δ E A
(b) S1 =
ℓ (2 √ 5 + 5)
2
(c) u = δ
2 + √ 5
4. Aufgabe
⎛
⎜
⎝
− cos β cosβ 1
− sin β − sin β 0
S2 =
−1 1 −2 cosβ
2 δ E A
ℓ (2 √ 5 + 5)
⎞⎛
⎟⎜
⎠⎝
S1
S2
S3
⎞
kein Fließen!
kein Fließen!
⎛
⎟ ⎜
⎠ = ⎝
S3 =
δ E A
ℓ (2 + √ 5)
−F/ √ 2
F/ √ 2
2 cosβ α ∆θ EA
⎞
⎟
⎠