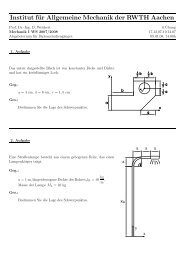
Musterlösung zur 8. ¨Ubung Mechanik II SS 07 Aufgabe 1:

Musterlösung zur 8. Übung Mechanik II SS 07
Aufgabe 1:
Schubspannungen infolge Querkraft:
Bei dünnwandigen Querschnitten t1, t2 ≪ b, h können die Schubspannungen in
Richtung der bereichsweise einzuführenden Laufkoordinaten si konstant über die
Bauteildicke angenommen werden. Die Schubspannungskomponente quer zu dieser
Richtung ist null. Es wirkt nur eine Querkraftkomponente in vertikaler Richtung
Qz = F.
τ(s) = − Qz
Iy t Sy(s) = − F
Iy t Sy(s)
Der Verlauf des Flächenmoments 1. Grades (statisches Moment) wird hier durch
Integration diskreter Werte gelöst. Aus der Definition der statischen Momente ist
sofort ersichtlich, dass ihr Verlauf jeweils um genau eine Ordnung höher ist als
derjenige der zu integrierenden Koordinate. Ist beispielsweise in einem Bereich die
z-Koordinate konstant, verläuft in diesem Bereich das statische Moment Sy linear
in s. Dabei ist s die für jeden Bereich einzuführende Laufkoordinate, die für den
jeweiligen Bereich die Integrationsrichtung angibt. Der Startwert für die Integration
in jedem Bereich muss bekannt sein, weshalb mit den Punkten begonnen wird, in
denen die Schubspannung null sein muss (auf der Symmetrie-Achse des Profils).
Aus der Betrachtung des Verlaufs der Koordinate z und Antragen der bekannten
Startwerte (Sy ist auf der Symmetrie-Achse null) ergibt sich sofort der Verlauf des
statischen Moments Sy, wobei ausserdem die Symmetrie des Profils berücksichtigt
wird.
z
− h/ 2 − − h/ 2
+
−
−
y
z
+
+
h/ 2 + h/ 2
+
+
−
−
1
S y
−
S y 2
S y

Dann brauchen nur noch die folgenden Randwerte durch Integration bestimmt zu
werden, wobei die Integrationsrichtung durch das Vorzeichen berücksichtigt werden
muss.
Sy(s) =
S 1 y =
�s
0
b/2
�
0
S 2 y = S1 y +
z(¯s) t d¯s
�
− h
�
2
�
h/2
Flächenmoment 2. Grades:
Iy = 2 t1 h3 + 2 bt2
12
0
t2 ds = − bht2
4
(−s) t1 ds = − bht2
4
� h
2
� 2
= t2 h 2
6
− t1
2
(2 h + 3 b)
� �2 h
= −
2
h
8 (2 bt2
h t2
+ h t1) = − (b + h)
4
Damit ergibt sich der folgende Schubspannungsverlauf infolge Querkraft.
−
− +
− +
τ 1 Q
τ 2 Q
+
τ 3
Q
τ
τ 1 Q =
=
τ2 Q = τ1 t2
Q
t1
τ 3 Q =
= 3 F (b + h)
6 F
t2 h 2 (2 h + 3 b) t2
3 F b
2 t2 h (2 h + 3 b)
=
bht2
4
3 F b
4 t2 h (2 h + 3 b)
6 F
t2 h 2 (2 h + 3 b) t1
4 t2 h (2 h + 3 b)
h t2
4
(b + h)

Schubspannungen infolge Torsion:
Bei dem doppeltsymmetrischen Querschnitt fallen Schubmittelpunkt und Flächen-
schwerpunkt zusammen. Allerdings greift die wirkende Querkraft nicht im Schub-
mittelpunkt an sondern um b/2 versetzt, wodurch das Torsionsmoment MT hervor-
gerufen wird.
MT =
F b
2
Die daraus resultierende Schubspannung lässt sich bereichsweise über die 1. Bredt’sche
Formel berechnen.
τi = MT
2 ti A
F b F
= =
4 ti bh 4 ti h
Damit lässt sich sofort der Schubspannungsverlauf infolge Torsion angeben.
τ 1
T
τ 2 T
+
τ 2 T
+
+
M = F b / 2
T
II
I
+
τ 1
T
τ
τ 1 T
τ 2 T
F F
= =
4 t1 h 8 t2 h
= F
4 t2 h
Die maximale Schubspannung herrscht dann je nach dem Verhältnis von b und h an
der Stelle I oder an der Stelle II. Die Schubspannungen aus Querkraft und Torsion
dürfen bei dünnwandigen Querschnitten superponiert werden.
τI = τ 1 T + τ3 Q
τII = τ 2 T + τ1 Q
F 3 F (b + h) F 8 h + 9 b
= + =
8 t2 h 4 t2 h (2 h + 3 b) 8 t2 h 2 h + 3 b
F
=
4 t2 h +
3 F b F 2 h + 9 b
=
2 t2 h (2 h + 3 b) 4 t2 h 2 h + 3 b

Aufgabe 2:
1. Bredt’sche Formel: MT = 2 τi ti A ; A =
τ1 = MT
2 s1 A
τ2 = MT
2 s2 A
4 MT N
= = 4974
2 s1 π d2 cm2 4 MT N
= = 2984
2 s2 π d2 cm2 2. Bredt’sche Formel: D = MT
4 G A2 ⇒ D = τi
�
si du
du = r dϕ
2 G A t(u)
� du
t(u) =
2π
3
�
0
⇒ D = ϕ
ℓ
r dϕ
+
s1
�2π
2π
3
= MT
4 G A 2
⇒ ϕ = 16 MT π d ℓ
12 G π 2 d 4
⇒ ϕ = 0, 784 ◦
r dϕ
s2
= 2 π r
� du
t(u)
� 1
s1
3 s1
+ 2
�
s2
+ 4 π r
= MT
4 G A 2
� du
t(u)
3 s2
π d
3
ϕ
= π d
� 1
r
3
s1
π d2
4
� 1
s1
+ 2
�
s2
00 11
00 11
00 11
u
+ 2
�
du
s2

Aufgabe 3:
Da die Schubspannungen vernachlässigt werden sollen und weder Längskraft noch
Torsion auftreten, muss nur die Biegespannung berechnet werden:
σb(x, y ′ , z ′ Mb,y ′(x)
) =
Iy ′
z ′ −
Mb,z ′(x)
Berechnung der Hauptflächenmomente Iy ′, Iz ′ und der Hauptachsen y’,z’
Iz ′
Zunächst werden für die drei rechteckigen Teilflächen, aus denen der Z-Querschnitt
zusammengesetzt ist, die Flächenmomente 2. Grades Iη,I, Iη,II, Iη,III und Iζ,I, Iζ,II,
Iζ,III bezüglich der jeweiligen Teilflächenschwerpunkte bestimmt. Mithilfe des Sat-
zes von Steiner können diese Einzelflächenmomente durch folgende Gleichungen auf
das KOS im Gesamtschwerpunkt transformiert werden, wobei yS1, yS2 die jeweiligen
Abstände der Einzelflächenschwerpunkte in y-Richtung und zS1, zS2 die jeweiligen
Abstände der Einzelflächenschwerpunkte in z-Richtung vom Gesamtflächenschwer-
punkt sind.
Iy = Iη + z 2 S A ,
����
Iz = Iζ + y
Steiner
2 S A
����
Steiner
Bestimmung des Gesamtflächenschwerpunkts:
�
(Ai ¯yi)
¯yS =
A
y ′
, Iyz = Iη ζ + yS zS A
¯yS = a2 · 0, 5 a + 3 a2 · 0, 5 a + 4 a2 · (−0, 5 a)
8 a2 = 0
�
(Ai ¯zi)
¯zS =
A
¯zS = a2 · (−1, 5 a) + 3 a 2 · (−0, 5 a) + 4 a 2 · 2 a
8 a 2
� �� �
Steiner
y
= 0, 625 cm
η 1
η2
ζ 2
y
η 3
ζ
1
ζ
3
I
a a
z, z
a
II
III
a
a
4a

Flächenmomente 2. Grades bezüglich des Schwerpunkts:
Iy = Iη,I + AI z 2 S1 + Iη,II + AII z 2 S2 + Iη,III + AIII z 2 S3
Iz = Iζ,I + AI y 2 S1 + Iζ,II + AII y 2 S2 + Iζ,III + AIII y 2 S3
Iyz = Iη ζ,I + AI yS1 zS1 + Iη ζ,II + AII yS2 zS2 + Iη ζ,III + AIII yS3 zS3 (3)
a · a3 1
Iη,I = =
12 12 cm4
3 a · a3 1
Iη,II = =
12 4 cm4
a · (4 a)3
Iη,III = =
12
16
3 cm4
Iη ζ,I = Iη ζ,II = Iη ζ,III = 0
Iζ,I = a3 · a
12
Iζ,II = (3 a)3 · a
12
Iζ,III = a3 · 4 a
12
= 1
12 cm4
= 9
4 cm4
= 1
3 cm4
zS1 = −(¯zS + 1, 5 a) = −2, 125 cm yS1 = 0, 5 a = 0, 5 cm A1 = a 2 = 1 cm 2
zS2 = −(¯zS + 0, 5 a) = −1, 125 cm yS2 = 0, 5 a = 0, 5 cm A2 = 3 a 2 = 3 cm 2
zS3 = 2 a − ¯zS = 1, 375 cm yS3 = −0, 5 a = −0, 5 cm A3 = 4 a 2 = 4 cm 2
Einsetzen in (1) , (2) und (3) ergibt:
Iy = 21, 54 cm 4 Iz = 4, 67 cm 4 Iyz = −5, 50 cm 4
Mohr’scher Trägheitskreis:
Analog zum Mohrschen Spannungskreis können jetzt mit der Zuordnung
(σy → Iy, σx → Iz, τ → Iyz)
mit Hilfe des Mohr’schen Trägheitskreises die Lage der Hauptachsen (Winkel ϕ) und
die Hauptflächenmomente 2. Grades I ′ y und I′ z (I′ yz
!
= 0) bestimmt werden. Alter-
nativ dazu können die Werte auch durch Auswertung der Formeln (6.47)-(6.49) aus
dem Skript berechnet werden.
(1)
(2)

Der Mohr’sche Trägheitskreis:
I
[cm
yz
4 ]
M b,z’
I
yz .
. 2ϕ .
.
(I z ;−I )
l
z ’
y
y’
ϕ
z
I y ’
(I ;I )
y yz
Iy ,Iz [cm4
]
Abgelesen:
ϕ = 16, 55 o
Iy ′ = 23, 18 cm4
Iz ′ = 3, 03 cm4
Zerlegung der Kraft F auf das y’, z’-Koordinatensystem
M b,y’
Ermittlung der Biegemomente an der Einspannstelle:
Mb,y ′ = Fz ′ ℓ
Mb,z ′ = Fy ′ ℓ
⇒ σb(x, y ′ , z ′ ) =
Fz ′ ℓ
Iy ′
Zahlenwerte einsetzen:
z ′ −
z’
x
F z’
Fy ′ ℓ
Iz ′
σb(x, y ′ , z ′ ) = 614, 51 N
cm3 z′ − 15806 N
y′
cm3 F y’
F
y ′
Fy ′ = F cosϕ = 958, 6 N
Fz ′ = F sin ϕ = 284, 8 N
F z’
F
F y’ ϕ

Bestimmung der maximalen Biegespannung
Gleichung der neutralen Achse:
σb(x, y ′ , z ′ ) = 614, 51 N
cm 3 z′ − 15806 N
cm 3 y′ ! = 0
⇒ 614, 51 z ′ = 15806 y ′
⇒ z ′ = 25, 72 y ′
P1: Punkt mit maximalem Abstand zur neutralen Achse
P 1
y
y’
ϕ
z
S
z’
neutrale
Achse
Im Hauptachsensystem:
P1 (1, 75 cm / − 1, 2 cm)
Maximale Druckspannung:
σb,1 = −28397, 6 N N
= −284, 0
cm2 mm2