Exploring the Methods of Differential Calculus through the ...

More documents

Recommendations

Info

Figure 8. Acceleration curves of the three candidate ramps. Candidate three has positive acceleration everywhere, meaning it is picking up speed as horizontal distance increases. Candidate two has zero acceleration, implying that it is traveling at a constant speed. Candidate one has negative acceleration values everywhere, meaning that it is slowing down as horizontal distance increases. It is however of note that the acceleration curves for both Candidate one and candidate three are increasing. In candidate one’s case, that implies that it is slowing down at a decreasing rate and in the case of candidate three, this observation implies that the ramp induces greater increases in speed as the bead progresses. Discussion Recall from equation (2) the momentum is proportional to the mass and the velocity. In this case, the bead has a fixed mass, meaning that the effect of mass on momentum can be ignored. Thus only velocity (Figure 6) can affect the momentum of the bead. The velocities of the bead for the cases studied are all negative. Since the velocities are all negative, the absolute value, speed (Figure 7), is used because it does not matter in which direction the bead travels, rather the rate of motion that it exhibits. This observation is how the speed of the bead affects the momentum of said bead. Having increased velocities earlier in the process allows for the stopping distance to contribute to achieving the target location in a quicker time. Recall from equation (3) that stopping distance is assumed to be for a flat surface, meaning that acceleration due to gravity would not have an effect on the stopping distance; however, the candidate ramps are not flat surfaces, so acceleration does have an effect on the stopping distance
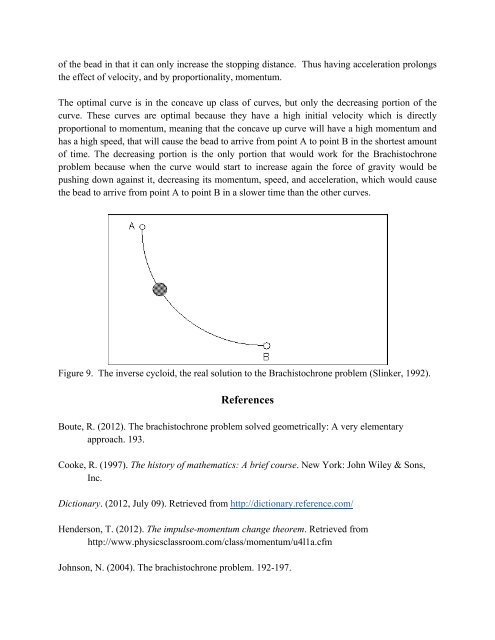
of the bead in that it can only increase the stopping distance. Thus having acceleration prolongs the effect of velocity, and by proportionality, momentum. The optimal curve is in the concave up class of curves, but only the decreasing portion of the curve. These curves are optimal because they have a high initial velocity which is directly proportional to momentum, meaning that the concave up curve will have a high momentum and has a high speed, that will cause the bead to arrive from point A to point B in the shortest amount of time. The decreasing portion is the only portion that would work for the Brachistochrone problem because when the curve would start to increase again the force of gravity would be pushing down against it, decreasing its momentum, speed, and acceleration, which would cause the bead to arrive from point A to point B in a slower time than the other curves. Figure 9. The inverse cycloid, the real solution to the Brachistochrone problem (Slinker, 1992). References Boute, R. (2012). The brachistochrone problem solved geometrically: A very elementary approach. 193. Cooke, R. (1997). The history of mathematics: A brief course. New York: John Wiley & Sons, Inc. Dictionary. (2012, July 09). Retrieved from http://dictionary.reference.com/ Henderson, T. (2012). The impulse-momentum change theorem. Retrieved from http://www.physicsclassroom.com/class/momentum/u4l1a.cfm Johnson, N. (2004). The brachistochrone problem. 192-197.
Page 1 and 2: Courtney Burris Mattanawcook Academ
Page 3 and 4: determination of slope: a measure o
Page 5 and 6: Figure 3. A concave up curve. Figur
Page 7 and 8: Figure 5. Graphs of the three candi
Page 9: Figure 7. Speed curves for the thre
Page 13: overwhelmed. First of all, I would

Exploring the Methods of Differential Calculus through the ...

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?