MAT 204 - INTRODUCTION TO STATISTICS - Chesapeake College
MAT 204 - INTRODUCTION TO STATISTICS - Chesapeake College
MAT 204 - INTRODUCTION TO STATISTICS - Chesapeake College
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
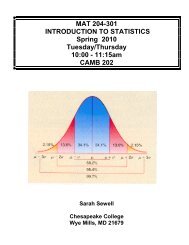
<strong>MAT</strong> <strong>204</strong><br />
<strong>INTRODUCTION</strong> <strong>TO</strong> <strong>STATISTICS</strong><br />
FALL 2009<br />
Brenda J. Bloomgarden<br />
Associate Professor - Mathematics<br />
<strong>Chesapeake</strong> <strong>College</strong><br />
Wye Mills, MD 21679
<strong>MAT</strong> <strong>204</strong> <strong>INTRODUCTION</strong> <strong>TO</strong> <strong>STATISTICS</strong> Fall 2009<br />
<strong>Chesapeake</strong> <strong>College</strong> Course Outcomes<br />
Course Number and Title: <strong>MAT</strong> <strong>204</strong>, Introduction to Statistics<br />
Program: General Education<br />
Students will be able to:<br />
Learning Outcomes<br />
1. Classify data and identify appropriate experimental designs<br />
2. Display data using graphs<br />
3. Use measures of central tendency and measures of variation<br />
4. Solve problems using probability rules.<br />
5. Solve application problems involving discrete probability distributions<br />
6. Use technology / tables to solve problems involving the normal distribution<br />
7. Draw conclusions or make predictions from data using inferential statistics.<br />
8. Use a graphing calculator and/or a computer program to solve statistical problems.<br />
Assessment Protocols: Homework<br />
Chapter Tests<br />
Group Projects<br />
Computer Project<br />
Final Exam<br />
Page 1
<strong>MAT</strong> <strong>204</strong> <strong>INTRODUCTION</strong> <strong>TO</strong> <strong>STATISTICS</strong> Fall 2009<br />
I. INSTRUC<strong>TO</strong>R: Mrs. Brenda Bloomgarden – <strong>College</strong> extension 328 (Voice Mail)<br />
Home: 410-778-0743 E-Mail: bbloomgarden@chesapeake.edu<br />
II. OFFICE HOURS Mondays & Wednesdays 11:30 am - 12:30 am Office LRC -107<br />
Tuesdays & Thursdays 11:30 am - 12:30 am Office LRC -107<br />
Tuesdays 2:30 – 3:30 pm Office LRC -107<br />
III. CLASS MEETING TIMES:<br />
<strong>MAT</strong> <strong>204</strong> - 101 Mondays & Wednesdays 10:00 am to 11:15 pm in room HEC -210<br />
<strong>MAT</strong> <strong>204</strong> - 102 Mondays & Wednesdays 1:00 pm to 2:15 pm in room HEC -210<br />
<strong>MAT</strong> <strong>204</strong> – 103 Tuesdays & Thursdays 10:00 pm to 11:15 pm in room HEC -210<br />
<strong>MAT</strong> <strong>204</strong> – 104 Tuesdays & Thursdays 1:00 pm to 2:15 pm in room HEC -210<br />
IV. COURSE DESCRIPTION:<br />
An introduction to probability and statistics. Topics included are probability, organization of<br />
data, sampling methods, measures of central tendency and variability, probability<br />
distributions, and hypothesis testing. Three hours per week, 3 credits.<br />
Prerequisite:<br />
Appropriate score on the mathematics placement test, or successful completion of <strong>MAT</strong> 032.<br />
V. TEXTBOOK:<br />
Elementary Statistics, Picturing the World, Fourth Edition, by Ron Larson and Betsy Farber,<br />
2009. Prentice-Hall, Inc., Upper Saddle River, NJ 07458. This textbook is bundled in a<br />
Special Package that includes the Student Study Pack and the MyMathLab.<br />
ISBN 0321587111<br />
VI. <strong>INTRODUCTION</strong>:<br />
The primary objective of this course, Introduction to Statistics, is to introduce some basic<br />
statistical concepts to college students. Since statistics has applications in many areas such as<br />
business, science, medicine, and education, examples have been substituted for mathematical<br />
proofs. Graphing calculators and computer software will be used to further illustrate many of<br />
the concepts.<br />
For this three-credit course the average student should plan to spend AT LEAST six hours<br />
per week outside of class working on assignments in addition to the in-class lectures.<br />
Students whose mathematics background is below average, or who normally work at a slower<br />
than average pace, should schedule more time in order to keep up with the course material. If<br />
you need extra help, please see me early in the semester. We would like to see you succeed<br />
and there is extra tutoring available.<br />
NOTE: <strong>College</strong> policy prohibits young children from accompanying parents to class.<br />
Page 2
<strong>MAT</strong> <strong>204</strong> <strong>INTRODUCTION</strong> <strong>TO</strong> <strong>STATISTICS</strong> Fall 2009<br />
VII. GRADES:<br />
This course consists of all or parts of chapters #1 through#10 in the assigned textbook. The<br />
following syllabus outlines in detail the material that will be presented from each of the<br />
chapters. The numerical final course grade will be computed as indicated in the following<br />
distribution, and letter grades will be assigned as follows.<br />
Components of Final Grade Letter Grade<br />
In-Class Activities 5% A : 90% - 100%<br />
Homework 5% B 80% - 89%<br />
Quiz Average 65% C : 70% - 79%<br />
Final Examination 25% D : 60% - 69%<br />
F : less than 60%<br />
VIII ATTENDANCE:<br />
Students whose attendance is sporadic often do not do well because of the nature of the<br />
course content. In addition, since attendance and participation constitute 5% of the<br />
student's final grade, (one-half of a letter grade) it is to the benefit of each student to be<br />
present at every class session. Most students need guidance in understanding the<br />
procedures involved in developing a new mathematical process and regular attendance<br />
tends to improve understanding. If you find yourself unable to keep up with the class,<br />
make an appointment to see the instructor outside of class time. It is the student's<br />
responsibility to make up any work missed due to an absence for any reason.<br />
IX. WRITING ASSIGNMENT:<br />
Consistent with <strong>Chesapeake</strong> <strong>College</strong>’s program of “Writing Across the Curriculum”,<br />
students will be expected to write properly formatted and informative essays to<br />
demonstrate understanding of various portions of the course material.<br />
X. TECHNOLOGY<br />
Students will be expected to use a TI-83+ or TI-84+ calculator for some assignments in<br />
this course. Also they will use the Microsoft Excel computer program to analyze and<br />
display data they have collected. Students who successfully complete the assigned<br />
“Computer Project” will have their lowest quiz grade omitted from the calculation of<br />
their “Quiz Average”.<br />
XI. TESTING:<br />
Dates for quizzes will be announced. Students are expected to be present for class on days<br />
for which quizzes are scheduled. Make up quizzes will be given only in the case of a<br />
documented emergency, and then will be scheduled and graded at the instructor's<br />
convenience. Students will have the opportunity to have a missed quiz grade, OR their<br />
lowest quiz grade omitted if they successfully complete the Computer Project.<br />
If a student is absent prior to a scheduled quiz, he/she will still be expected to take<br />
the quiz at the scheduled time and is expected to contact a classmate or the<br />
instructor to obtain the information required in order to prepare for the quiz.<br />
Page 3
<strong>MAT</strong> <strong>204</strong> <strong>INTRODUCTION</strong> <strong>TO</strong> <strong>STATISTICS</strong> Fall 2009<br />
<strong>MAT</strong> <strong>204</strong> - <strong>INTRODUCTION</strong> <strong>TO</strong> <strong>STATISTICS</strong><br />
COURSE OUTLINE<br />
Chapter <strong>TO</strong>PIC Pages<br />
One Introduction to Statistics 1 - 37<br />
Two Descriptive Statistics 38 - 137<br />
Three Probability 128 - 191<br />
Four Discrete Probability Distributions 192 - 237<br />
Five Normal Probability Distributions 238 - 305<br />
Six Confidence Intervals 306 - 361<br />
Seven Hypothesis Testing with One Sample 362 - 435<br />
Eight Hypothesis Testing with Two Samples 436 - 491<br />
Nine Correlation and Regression 492 - 549<br />
Ten Chi Square Tests and the F-Distribution 550 - 609<br />
Course Review and Final Examination All Chapters<br />
The quizzes will cover the subject matter of each chapter, and quizzes for specific sections may be<br />
combined so as to maximize course effectiveness. The above outline may be modified slightly as<br />
necessary to accommodate student needs and to permit possible computer and/or video<br />
demonstrations.<br />
A brief description of the Objectives for each chapter and the Homework Assignments are detailed<br />
on the following pages.<br />
Homework Assignments will be due before each quiz or as requested by the instructor and will<br />
include those sections covered in the previous class lecture. It is expected that each student will be<br />
able to solve ALL of the exercise problems in each section covered, even though only part of the<br />
exercise problems are specifically assigned.<br />
Homework is to be legible and for each problem the homework should include given data, any<br />
required calculations and the final answer. Credit will not be given for answers only. The answers<br />
to the odd numbered problems are given in the back of the textbook, and the complete solutions to<br />
most of them are presented in the “Student Solutions Manual”.<br />
Page 4
<strong>MAT</strong> <strong>204</strong> <strong>INTRODUCTION</strong> <strong>TO</strong> <strong>STATISTICS</strong> Fall 2009<br />
CHAPTER OBJECTIVES<br />
After completing each chapter the student should be able to accomplish the following:<br />
Chapter One Introduction to Statistics<br />
OBJECTIVES:<br />
a. Define statistics.<br />
b. Distinguish between a population and a sample and between a parameter and a statistic.<br />
c. Distinguish between descriptive statistics and inferential statistics.<br />
d. Distinguish between qualitative data and quantitative data.<br />
e. Classify data with respect to the four levels of measurement: nominal, ordinal, interval, and<br />
ratio.<br />
f. Identify the characteristics of a confounding variable, blind experiment, double-blind<br />
experiment, randomization, and replication in an experimental design<br />
g. Design a statistical study.<br />
h. Collect data by performing an experiment, using a simulation, taking a census, or using a<br />
sample.<br />
i. Create a sample using random sampling, stratified sampling, cluster sampling, systematic<br />
sampling, and convenience sampling.<br />
HOMEWORK ASSIGNMENT:<br />
NOTE: Work must be shown for each problem to receive full credit for your homework!<br />
Complete the following assigned exercises at the end of each section.<br />
Sec. 1.1 Problems #1-4, 7-10, 11-14, 18,25-28, 31, 32, 37, 38 Pages 8 - 10<br />
Sec. 1.2 Problems #2-5, 9-12, 13, 16, 18, 21-24 Pages 15 - 16<br />
Sec. 1.3 Problems #1-4, 6-9, 11-14, 15, 18-22, 29, 30, 33, 34 Pages 25 - 27<br />
Page 5
<strong>MAT</strong> <strong>204</strong> <strong>INTRODUCTION</strong> <strong>TO</strong> <strong>STATISTICS</strong> Fall 2009<br />
CHAPTER OBJECTIVES - (Continued)<br />
Chapter Two Descriptive Statistics<br />
OBJECTIVES:<br />
a. Construct a frequency distribution including midpoints, relative frequencies, and<br />
cumulative frequencies.<br />
b. Construct frequency histograms, frequency polygons, relative frequency histograms, and<br />
cumulative frequency graphs (ogives).<br />
c. Graph quantitative data sets using stem-and-leaf plots and dot plots.<br />
d. Graph qualitative data using pie charts and Pareto charts.<br />
e. Graph paired data sets using scatter plots and time series charts.<br />
f. Find the mean, median, and mode of a population and a sample.<br />
g. Find the weighted mean and the mean of the frequency distribution.<br />
h. Describe the shape of a distribution as symmetric, uniform, or skewed.<br />
i. Find the range of a set of data.<br />
j. Find the variance and the standard deviation of a population and of a sample.<br />
k. Use the Empirical Rule and Chebychev's Theorem to interpret standard deviation.<br />
l. Approximate the sample standard deviation for grouped data.<br />
m. Find the first, second, and third quartiles of a data set.<br />
n. Find the interquartile range of a data set.<br />
o. Represent a data set graphically using a box-and-whisker plot.<br />
p. Interpret other fractiles such as percentiles and deciles.<br />
HOMEWORK ASSIGNMENT:<br />
NOTE: Work must be shown for each problem to receive full credit for your homework!<br />
Complete the following assigned exercises at the end of each section.<br />
Sec. 2.1 Problems #1-10, 14, 16, 17, 19-21, 25-27, 30, 37, 38, 41 Pages 49 - 53<br />
Sec. 2.2 Problems #1, 2, 4-10, 13, 14, 17, 18, 23, 24, 29, 30 Pages 62 - 65<br />
Sec. 2.3 Problems #1-10,13, 14, 17, 18, 23, 26, 35-37, 41, 42, 47, 48<br />
Pages 74 - 78<br />
Sec. 2.4 Problems #1-10, 13, 14, 17, 18, 23, 24, 27-32, 35-37, 43, 45, 46*, 51<br />
* Use data from problem #3, instead of problem #21 Pages 92 - 99<br />
Sec. 2.5 Problems #1-12, 21, 22, 29-35, Pages 109 - 112<br />
Page 6
<strong>MAT</strong> <strong>204</strong> <strong>INTRODUCTION</strong> <strong>TO</strong> <strong>STATISTICS</strong> Fall 2009<br />
CHAPTER OBJECTIVES - (Continued)<br />
Chapter Three Probability<br />
OBJECTIVES:<br />
a. Identify the sample space of a probability experiment and identify simple events.<br />
b. Use the Fundamental Counting Principle to find the number of ways two or more events<br />
can occur.<br />
c. Distinguish among classical probability, empirical probability, and subjective probability.<br />
d. Use Tree Diagrams or The Fundamental Counting Principle for probability applications<br />
e. Identify and use properties of probability.<br />
f. Find the probability of an event given that another event has occurred.<br />
g. Distinguish between independent events and dependent events.<br />
h. Use the multiplication rule to find the probability of two events occurring in sequence.<br />
i. Use the multiplication rule to find conditional probabilities.<br />
j. Determine if two events are mutually exclusive.<br />
k. Use the addition rule to find the probability of two events.<br />
l. Find the number of ways a group of objects can be arranged in order. (permutations)<br />
m. Find the number of ways to choose several objects from a group without regard to order.<br />
(combinations)<br />
n. Use counting principles to find probabilities.<br />
HOMEWORK ASSIGNMENT:<br />
NOTE: Work must be shown for each problem to receive full credit for your homework!<br />
Complete the following assigned exercises at the end of each section.<br />
Sec. 3.1 Problems #1-8, 11-16, 18, 20, 21-24, 27-30, 31-34,<br />
41 (see #37-#40), 44, 46, 48, 52, 55, 57, 60, 64-67 Pages 142 – 147<br />
Sec. 3.2 Problems #1-8, 9, 11, 13, 15, 16, 17, 21-25, 27, 37, 38 Pages 154 - 159<br />
Sec. 3.3 Problems #1-4, 9-10, 13-15, 20, 21, 23, 24, 29 Pages 165 - 169<br />
Sec. 3.4 Problems #1-6, 9-12(show work), 15-17, 19-21, 23-27,<br />
29, 32, 36, 43 Pages 178 - 182<br />
Page 7
<strong>MAT</strong> <strong>204</strong> <strong>INTRODUCTION</strong> <strong>TO</strong> <strong>STATISTICS</strong> Fall 2009<br />
CHAPTER OBJECTIVES - (Continued)<br />
Chapter Four Discrete Probability Distributions<br />
OBJECTIVES:<br />
a. Distinguish between discrete random variables and continuous random variables.<br />
b. Construct a discrete probability distribution and its graph.<br />
c. Determine if a distribution is a probability distribution.<br />
d. Find the mean, variance, and standard deviation of a discrete probability distribution.<br />
e. Find the expected value of a probability distribution.<br />
f. Determine if a probability experiment is a binomial experiment.<br />
g. Find binomial probabilities using the binomial probability formula, a binomial probability<br />
table, and technology.<br />
h. Construct a binomial distribution and its graph.<br />
i. Find the mean, variance, and standard deviation of a binomial probability distribution.<br />
j. Find probabilities using the geometric distribution.<br />
k. Find probabilities using the Poisson distribution.<br />
HOMEWORK ASSIGNMENT:<br />
NOTE: Work must be shown for each problem to receive full credit for your homework!<br />
Complete the following assigned exercises at the end of each section.<br />
Sec. 4.1 Problems #1, 2, 5-8, 11, 12, 15-18, 21-28, 31, 32, 35, 38, 45, 47, 49<br />
Pages 201 - 205<br />
Sec. 4.2 Problems #1, 3, 7-9, 15-17, 22, 26, 27 pages 215 - 218<br />
Sec. 4.3 Problems # 1, 2, 5, 6, 11-14, 17, 20-23, 25, 27 pages 226 - 228<br />
Page 8
<strong>MAT</strong> <strong>204</strong> <strong>INTRODUCTION</strong> <strong>TO</strong> <strong>STATISTICS</strong> Fall 2009<br />
CHAPTER OBJECTIVES - (Continued)<br />
Chapter Five Normal Probability Distributions<br />
OBJECTIVES:<br />
a. Interpret graphs of normal probability distributions.<br />
b. Find areas under a normal curve, and use them to find probabilities for random variables<br />
with normal distributions.<br />
c. Find and interpret standard z-scores and find the value of a variable when its standard score<br />
is given.<br />
d. Find areas under the standard normal curve and find areas under any normal curve using a<br />
table.<br />
e. Compare data from two normal distributions.<br />
f. Find probabilities for normally distributed variables using a table and using technology.<br />
g. Find a specific data entry of a normal distribution given the probability.<br />
h. Find sampling distributions and verify their properties.<br />
i. Interpret the Central Limit Theorem.<br />
j. Apply the Central Limit Theorem to find the probability of a sample mean.<br />
k. Decide when the normal distribution can approximate the binomial distribution.<br />
l. Find the correction for continuity.<br />
m. Use the normal distribution to approximate binomial probabilities.<br />
HOMEWORK ASSIGNMENT:<br />
NOTE: Work must be shown for each problem to receive full credit for your homework!<br />
Complete the following assigned exercises at the end of each section.<br />
Sec. 5.1 Problems # 1-12, 15-40, 43-62 pages 248 - 252<br />
Sec. 5.2 Problems # 1-8, 13, 14, 17, 18, 21, 22, 27, 28, 31, 32 pages 256 - 260<br />
Sec. 5.3 Problems # 1-4, 14-17, 25-41, 47 pages 266 - 268<br />
Sec. 5.4 Problems # 1- 8, 10-14, 17, 21, 25-27, 29, 30, 33, 34, 41, 42<br />
pages 278 - 283<br />
Sec. 5.5 Problems # 1-6, 9-17, 21, 22, 26, 29 pages 291 – 294<br />
Page 9
<strong>MAT</strong> <strong>204</strong> <strong>INTRODUCTION</strong> <strong>TO</strong> <strong>STATISTICS</strong> Fall 2009<br />
CHAPTER OBJECTIVES - (Continued)<br />
Chapter Six Confidence Intervals<br />
OBJECTIVES:<br />
a. Find a point estimate and a maximum error of estimate.<br />
b. Construct and interpret confidence intervals for the population mean.<br />
c. Determine the required minimum sample size when estimating .<br />
d. Interpret the t-distribution and use a t-distribution table.<br />
e. Construct confidence intervals when n < 30 and is unknown.<br />
f. Find a sample proportion.<br />
g. Construct a confidence interval for a population proportion.<br />
h. Determine a minimum sample size when estimating a population proportion.<br />
i. Interpret the chi-square distribution and use a chi-square distribution table.<br />
j. Use the chi-square distribution to construct a confidence interval for the variance and<br />
standard deviation.<br />
HOMEWORK ASSIGNMENT:<br />
NOTE: Work must be shown for each problem to receive full credit for your homework!<br />
Complete the following assigned exercises at the end of each section.<br />
Sec. 6.1 Problems #1-10, 15, 16, 19-24, 29, 30, 33, 34, 39-41,<br />
43, 51, 53, 54, 60, 69 Pages 317 - 323<br />
Sec. 6.2 Problems #1-6, 9, 10, 13-15, 18, 21, 22, 24, 27, 29 Pages 330 - 332<br />
Sec. 6.3 Problems #1-6, 13-18, 21, 22, 27, 28a, 33 Pages 339 - 342<br />
Sec, 6.4 Problems #1- 4, 8, 9, 22 Pages 348 - 350<br />
Page 10
<strong>MAT</strong> <strong>204</strong> <strong>INTRODUCTION</strong> <strong>TO</strong> <strong>STATISTICS</strong> Fall 2009<br />
CHAPTER OBJECTIVES - (Continued)<br />
Chapter Seven Hypothesis Testing with One Sample<br />
OBJECTIVES:<br />
a. Identify the characteristics of a hypothesis test.<br />
b. State the null hypothesis and the alternative hypothesis<br />
c. Identify type I and type II errors and interpret the level of significance.<br />
d. Determine when to use a one-tailed or a two-tailed statistical test.<br />
e. Make a decision based on the results of a statistical test.<br />
f. Write a claim for a hypothesis test.<br />
g. Find critical values in a normal distribution.<br />
h. Use the z-test to test a mean .<br />
i. Find P-values and use them to test a mean .<br />
j. Find critical values in a t-distribution.<br />
k. use the t-test to test a mean .<br />
l. Use technology to find P-values and use them to test a mean .<br />
m. Use the z-test to test a population proportion p.<br />
n. Find the critical values for a 2 - test.<br />
o. Use the 2 - test to test a variance or a standard deviation.<br />
HOMEWORK ASSIGNMENT:<br />
NOTE: Work must be shown for each problem to receive full credit for your homework !<br />
Complete the following assigned exercises at the end of each section.<br />
Sec. 7.1 Problems #1-21, 23, 25, 29, 30 35, 36, 41, 42, 47, 49, 53, 54<br />
Pages 375 - 378<br />
Sec. 7.2 Problems #1-26, 29, 30, 33, 34, 39, 40 Pages 389 - 392<br />
Sec. 7.3 Problems #1-8, 15, 16, 19, 20, 23, 24, 29, 37 Pages 403 - 406<br />
Sec. 7.4 Problems #1-5, 9, 10, 13 Pages 411 - 412<br />
Sec. 7.5 Problems #1-7, 9-11, 13-15 Pages 420 – 421<br />
Page 11
<strong>MAT</strong> <strong>204</strong> <strong>INTRODUCTION</strong> <strong>TO</strong> <strong>STATISTICS</strong> Fall 2009<br />
CHAPTER OBJECTIVES - (Continued)<br />
Chapter Eight Hypothesis Testing with Two Samples<br />
OBJECTIVES:<br />
a. Identify the characteristics of two-sample hypothesis testing for the difference between two<br />
population parameters.<br />
b. Perform a two-sample z-test for the difference between two means, 1 and 2 using large<br />
independent samples.<br />
c. Perform a t-test for the difference between two population means, 1 and 2 using small<br />
independent samples.<br />
d. Decide whether two samples are independent or dependent.<br />
e. Perform a t-test to test the mean of the differences for a population of paired data.<br />
f. Perform a z-test for the difference between two population proportions p 1 and p 2 .<br />
HOMEWORK ASSIGNMENT:<br />
NOTE: Work must be shown for each problem to receive full credit for your homework !<br />
Complete the following assigned exercises at the end of each section.<br />
Sec. 8.1 Problems #1-6, 13, 14, 17, 19, 20 35, 39 Pages 444 - 450<br />
Sec. 8.2 Problems #1-5, 11, 13-15, 25 Pages 456 - 460<br />
Sec. 8.3 Problems #1-4, 13, 14 Pages 466 - 468<br />
Sec. 8.4 Problems #1-4, 7, 8, 25 Pages 475 - 478<br />
Page 12
<strong>MAT</strong> <strong>204</strong> <strong>INTRODUCTION</strong> <strong>TO</strong> <strong>STATISTICS</strong> Fall 2009<br />
CHAPTER OBJECTIVES - (Continued)<br />
Chapter Nine Correlation and Regression<br />
OBJECTIVES:<br />
a. Describe linear correlation, independent and dependent variables, and the types of<br />
correlation.<br />
b. Find a correlation coefficient.<br />
c. Perform a hypothesis test for a population correlation coefficient .<br />
d. Find the equation of a regression line.<br />
e. Predict y-values using a regression equation.<br />
f. Interpret the three types of variation about a regression line.<br />
g. Find and interpret the coefficient of determination.<br />
h. Find and interpret the standard error of estimate for a regression line.<br />
i. Construct and interpret a prediction interval for y.<br />
j. Use technology to find a multiple regression equation.<br />
k. Use a multiple regression equation to predict y-values.<br />
HOMEWORK ASSIGNMENT:<br />
NOTE: Work must be shown for each problem to receive full credit for your homework !<br />
Complete the following assigned exercises at the end of each section.<br />
Sec. 9.1 Problems #1, 2, 4, 5-8, 13-15, 17 Pages 507 - 508<br />
Sec. 9.2 Problems #1-13, 18 Pages 517 - 519<br />
Sec. 9.3 Problems #1-6, 13, 21 Pages 531 - 534<br />
Sec. 9.4 Review the problems in the Student Solutions Manual. Pages 539 - 540<br />
Chapter Ten Chi Square Tests and the F-Distribution<br />
OBJECTIVES:<br />
a. Use the chi-square distribution to test whether a frequency distribution fits a claimed<br />
distribution.<br />
b. Use a contingency table to find expected frequencies.<br />
c. Use a chi-square distribution to test whether two variables are independent.<br />
d. Interpret the F-distribution and use an F-table to find critical values.<br />
e. Perform a two-sample F-test to compare two variances.<br />
f. Use one-way analysis of variance to test claims involving three or more means.<br />
g. Describe a two-way analysis of variance.<br />
HOMEWORK ASSIGNMENT:<br />
Sec. 10.1<br />
Sec. 10.2<br />
Sec. 10.3 <strong>TO</strong> BE ASSIGNED IN CLASS<br />
Sec. 10.4<br />
Page 13