Comparison of bisector-point and double-angle-bisect draw systems
Comparison of bisector-point and double-angle-bisect draw systems
Comparison of bisector-point and double-angle-bisect draw systems
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
technical pro<strong>of</strong><br />
technical pro<strong>of</strong><br />
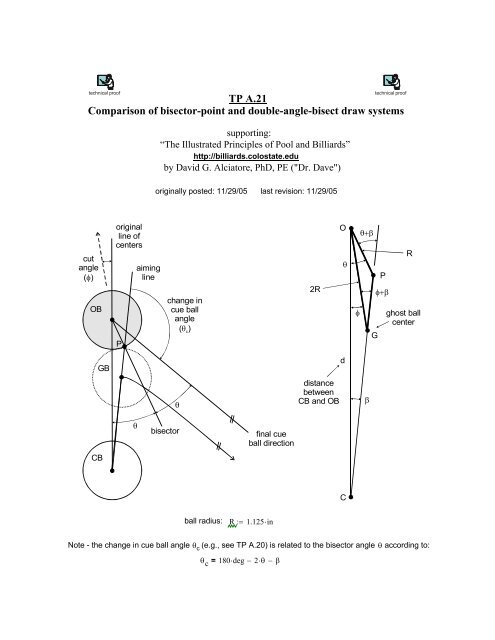
TP A.21<br />
<strong>Comparison</strong> <strong>of</strong> <strong><strong>bisect</strong>or</strong>-<strong>point</strong> <strong>and</strong> <strong>double</strong>-<strong>angle</strong>-<strong>bisect</strong> <strong>draw</strong> <strong>systems</strong><br />
cut<br />
<strong>angle</strong><br />
( φ)<br />
OB<br />
CB<br />
GB<br />
original<br />
line <strong>of</strong><br />
centers<br />
P<br />
θ<br />
aiming<br />
line<br />
supporting:<br />
“The Illustrated Principles <strong>of</strong> Pool <strong>and</strong> Billiards”<br />
http://billiards.colostate.edu<br />
by David G. Alciatore, PhD, PE ("Dr. Dave")<br />
originally posted: 11/29/05 last revision: 11/29/05<br />
change in<br />
cue ball<br />
<strong>angle</strong><br />
( θc) θ<br />
<strong><strong>bisect</strong>or</strong><br />
final cue<br />
ball direction<br />
ball radius: R := 1.125⋅in 2R<br />
distance<br />
between<br />
CB <strong>and</strong> OB<br />
O<br />
θ<br />
d<br />
C<br />
φ<br />
θ+β<br />
β<br />
G<br />
P<br />
φ+β<br />
R<br />
ghost ball<br />
center<br />
Note - the change in cue ball <strong>angle</strong> θ c (e.g., see TP A.20) is related to the <strong><strong>bisect</strong>or</strong> <strong>angle</strong> θ according to:<br />
θc =<br />
180⋅deg − 2⋅θ − β
From the tri<strong>angle</strong> formed by C, P, <strong>and</strong> the perpendicular from P to OC,<br />
tan( β)<br />
βθd ,<br />
( )<br />
( )<br />
R⋅sin θ<br />
=<br />
d − R⋅cos θ<br />
( ) := atan2( d − R⋅cos( θ)<br />
, R⋅sin( θ)<br />
)<br />
Applying the law <strong>of</strong> sines to tri<strong>angle</strong> OGP gives:<br />
⎡⎣ ( ) ⎤⎦<br />
sin 180⋅deg − θ + β<br />
φθ, d<br />
2R ⋅<br />
( ) ⎛<br />
:= asin⎜ ⎝<br />
=<br />
sin θ β θ d , +<br />
sin( φ + β)<br />
R<br />
( ( ) ) ⎞<br />
2 ⎠<br />
−<br />
βθd ( , )<br />
The <strong>double</strong>-<strong>angle</strong>-<strong>bisect</strong> system (see Bob Jewett's October, 1995 BD article) predicts:<br />
φ ( dab θ)<br />
θ<br />
:=<br />
2<br />
Here's how the methods compare for two different CB-OB distances:<br />
d1 := 1ft ⋅<br />
d2 := 6ft ⋅<br />
θ := 0⋅deg .. 60⋅deg φ<br />
dab<br />
( θ)<br />
deg<br />
( )<br />
φθd ,<br />
1<br />
deg<br />
( )<br />
φθd ,<br />
2<br />
deg<br />
30<br />
20<br />
10<br />
0<br />
0 20 40 60<br />
So the two <strong>systems</strong> agree fairly well for small cut <strong>angle</strong> shots. There is more disagrement<br />
at bigger cut <strong>angle</strong>s, especially when the distance between the CB <strong>and</strong> OB is large.<br />
θ<br />
deg