Dynamic properties of shear thickening colloidal suspensions

206
Fig. 9 Lissajous plot for aqueous silica dispersion at 60 vol.% and
a frequency of 0.1 rad/s and the applied stress amplitude of 5 Pa
which is relatively low
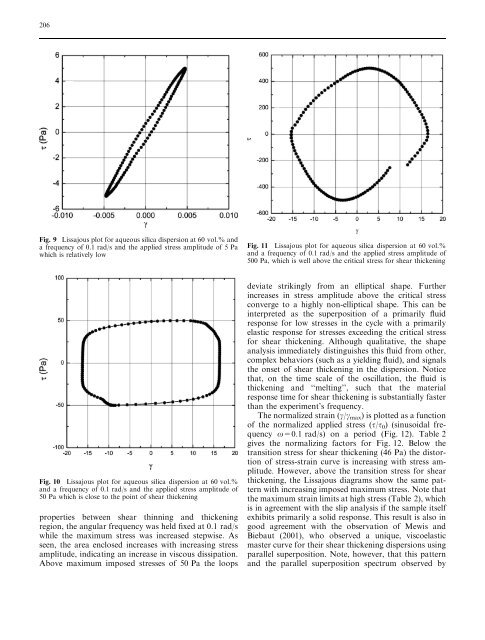
Fig. 10 Lissajous plot for aqueous silica dispersion at 60 vol.%
and a frequency of 0.1 rad/s and the applied stress amplitude of
50 Pa which is close to the point of shear thickening
properties between shear thinning and thickening
region, the angular frequency was held fixed at 0.1 rad/s
while the maximum stress was increased stepwise. As
seen, the area enclosed increases with increasing stress
amplitude, indicating an increase in viscous dissipation.
Above maximum imposed stresses of 50 Pa the loops
Fig. 11 Lissajous plot for aqueous silica dispersion at 60 vol.%
and a frequency of 0.1 rad/s and the applied stress amplitude of
500 Pa, which is well above the critical stress for shear thickening
deviate strikingly from an elliptical shape. Further
increases in stress amplitude above the critical stress
converge to a highly non-elliptical shape. This can be
interpreted as the superposition of a primarily fluid
response for low stresses in the cycle with a primarily
elastic response for stresses exceeding the critical stress
for shear thickening. Although qualitative, the shape
analysis immediately distinguishes this fluid from other,
complex behaviors (such as a yielding fluid), and signals
the onset of shear thickening in the dispersion. Notice
that, on the time scale of the oscillation, the fluid is
thickening and ‘‘melting’’, such that the material
response time for shear thickening is substantially faster
than the experiment’s frequency.
The normalized strain (c/cmax) is plotted as a function
of the normalized applied stress (s/s0) (sinusoidal frequency
x=0.1 rad/s) on a period (Fig. 12). Table 2
gives the normalizing factors for Fig. 12. Below the
transition stress for shear thickening (46 Pa) the distortion
of stress-strain curve is increasing with stress amplitude.
However, above the transition stress for shear
thickening, the Lissajous diagrams show the same pattern
with increasing imposed maximum stress. Note that
the maximum strain limits at high stress (Table 2), which
is in agreement with the slip analysis if the sample itself
exhibits primarily a solid response. This result is also in
good agreement with the observation of Mewis and
Biebaut (2001), who observed a unique, viscoelastic
master curve for their shear thickening dispersions using
parallel superposition. Note, however, that this pattern
and the parallel superposition spectrum observed by