A Numerical Renormalization Group Approach to Dissipative ...

14.5.3 Multiple Phonon Excitations 157
ometer
ReGLR/(g 2 ph e2 ¯h −1 )
25
20
15
10
5
0
gph = 0.033W
-5
0 0.5 1 1.5 2
ωac/ε
f(ε) ≈ n(ε) = n↑ + n↓. (14.30)
Γ/W =
0.0025
0.005
0.01
0.02
ReGLR/(g 2 ph e2 ¯h −1 )
30
25
20
15
10
5
0
gph = 0.05W
-5
0 0.5 1 1.5 2
ωac/ε
Γ/W =
0.0025
0.005
0.01
0.02
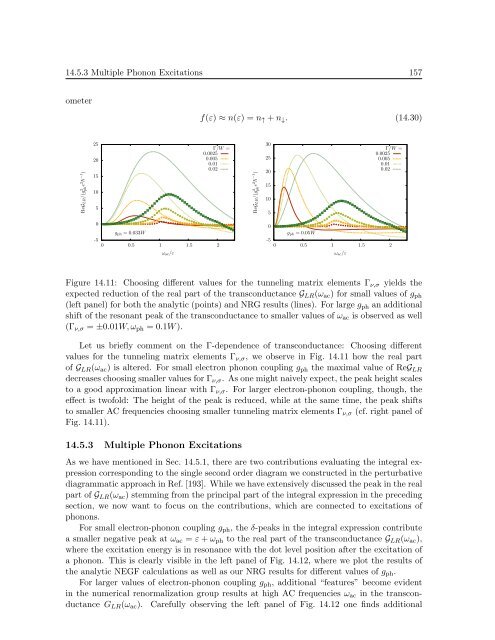
Figure 14.11: Choosing different values for the tunneling matrix elements Γν,σ yields the
expected reduction of the real part of the transconductance GLR(ωac) for small values of gph
(left panel) for both the analytic (points) and NRG results (lines). For large gph an additional
shift of the resonant peak of the transconductance to smaller values of ωac is observed as well
(Γν,σ = ±0.01W, ωph = 0.1W ).
Let us briefly comment on the Γ-dependence of transconductance: Choosing different
values for the tunneling matrix elements Γν,σ, we observe in Fig. 14.11 how the real part
of GLR(ωac) is altered. For small electron phonon coupling gph the maximal value of ReGLR
decreases choosing smaller values for Γν,σ. As one might naively expect, the peak height scales
to a good approximation linear with Γν,σ. For larger electron-phonon coupling, though, the
effect is twofold: The height of the peak is reduced, while at the same time, the peak shifts
to smaller AC frequencies choosing smaller tunneling matrix elements Γν,σ (cf. right panel of
Fig. 14.11).
14.5.3 Multiple Phonon Excitations
As we have mentioned in Sec. 14.5.1, there are two contributions evaluating the integral expression
corresponding to the single second order diagram we constructed in the perturbative
diagrammatic approach in Ref. [193]. While we have extensively discussed the peak in the real
part of GLR(ωac) stemming from the principal part of the integral expression in the preceding
section, we now want to focus on the contributions, which are connected to excitations of
phonons.
For small electron-phonon coupling gph, the δ-peaks in the integral expression contribute
a smaller negative peak at ωac = ε + ωph to the real part of the transconductance GLR(ωac),
where the excitation energy is in resonance with the dot level position after the excitation of
a phonon. This is clearly visible in the left panel of Fig. 14.12, where we plot the results of
the analytic NEGF calculations as well as our NRG results for different values of gph.
For larger values of electron-phonon coupling gph, additional “features” become evident
in the numerical renormalization group results at high AC frequencies ωac in the transconductance
GLR(ωac). Carefully observing the left panel of Fig. 14.12 one finds additional