Cluj polynomials

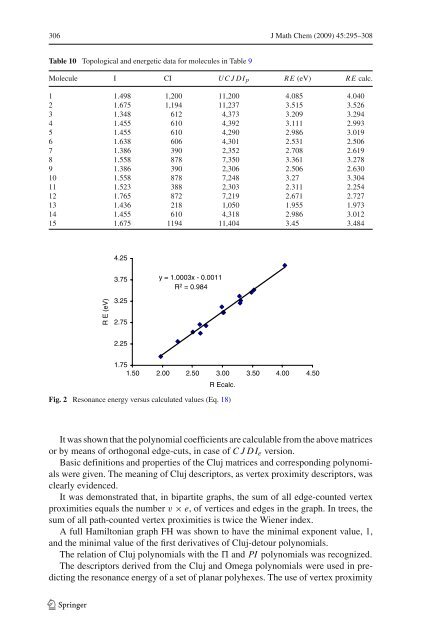
306 J Math Chem (2009) 45:295–308
Table 10 Topological and energetic data for molecules in Table 9
Molecule I CI UCJDIp RE (eV) RE calc.
1 1.498 1,200 11,200 4.085 4.040
2 1.675 1,194 11,237 3.515 3.526
3 1.348 612 4,373 3.209 3.294
4 1.455 610 4,392 3.111 2.993
5 1.455 610 4,290 2.986 3.019
6 1.638 606 4,301 2.531 2.506
7 1.386 390 2,352 2.708 2.619
8 1.558 878 7,350 3.361 3.278
9 1.386 390 2,306 2.506 2.630
10 1.558 878 7,248 3.27 3.304
11 1.523 388 2,303 2.311 2.254
12 1.765 872 7,219 2.671 2.727
13 1.436 218 1,050 1.955 1.973
14 1.455 610 4,318 2.986 3.012
15 1.675 1194 11,404 3.45 3.484
R E (eV)
4.25
3.75
3.25
2.75
2.25
y = 1.0003x - 0.0011
R 2 = 0.984
1.75
1.50 2.00 2.50 3.00
R Ecalc.
3.50 4.00 4.50
Fig. 2 Resonance energy versus calculated values (Eq. 18)
It was shown that the polynomial coefficients are calculable from the above matrices
or by means of orthogonal edge-cuts, in case of CJDIe version.
Basic definitions and properties of the Cluj matrices and corresponding polynomials
were given. The meaning of Cluj descriptors, as vertex proximity descriptors, was
clearly evidenced.
It was demonstrated that, in bipartite graphs, the sum of all edge-counted vertex
proximities equals the number v × e, of vertices and edges in the graph. In trees, the
sum of all path-counted vertex proximities is twice the Wiener index.
A full Hamiltonian graph FH was shown to have the minimal exponent value, 1,
and the minimal value of the first derivatives of Cluj-detour polynomials.
The relation of Cluj polynomials with the and PI polynomials was recognized.
The descriptors derived from the Cluj and Omega polynomials were used in predicting
the resonance energy of a set of planar polyhexes. The use of vertex proximity
123