On a forcing model for non-standard arithmetic
On a forcing model for non-standard arithmetic
On a forcing model for non-standard arithmetic
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
Sheaf semantics A <strong>non</strong>-principal ultrafilter A <strong><strong>for</strong>cing</strong> <strong>model</strong> <strong>for</strong> <strong>non</strong>-<strong>standard</strong> <strong>arithmetic</strong> Open questions<br />
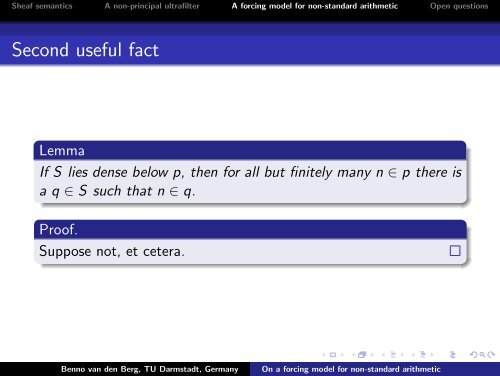
Second useful fact<br />
Lemma<br />
If S lies dense below p, then <strong>for</strong> all but finitely many n ∈ p there is<br />
a q ∈ S such that n ∈ q.<br />
Proof.<br />
Suppose not, et cetera.<br />
Benno van den Berg, TU Darmstadt, Germany <strong>On</strong> a <strong><strong>for</strong>cing</strong> <strong>model</strong> <strong>for</strong> <strong>non</strong>-<strong>standard</strong> <strong>arithmetic</strong>