Physics 9 Fall 2011 Homework 4 - Solutions Friday September 16 ...

Physics 9 Fall 2011
Homework 4 - Solutions
Friday September 16, 2011
Make sure your name is on your homework, and please box your final answer. Because
we will be giving partial credit, be sure to attempt all the problems, even if you don’t finish
them. The homework is due at the beginning of class on Friday, September 23rd. Because
the solutions will be posted immediately after class, no late homeworks can be accepted! You
are welcome to ask questions during the discussion session or during office hours.
1. The potential energy between
a pair of neutral
atoms or molecules is very
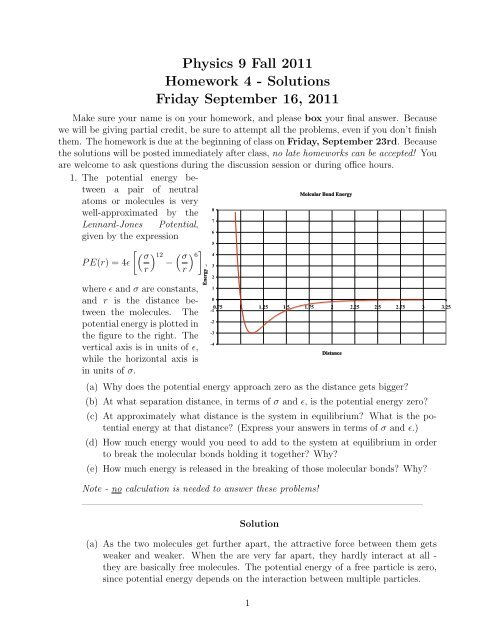
Molcular Bond Energy
well-approximated by the
8
Lennard-Jones Potential,
7
given by the expression
6
5
σ 12
σ
6 4
P E(r) = 4ɛ − , 3
r r
where ɛ and σ are constants,
and r is the distance between
the molecules. The
potential energy is plotted in
the figure to the right. The
vertical axis is in units of ɛ,
while the horizontal axis is
in units of σ.
Energy
2
1
0
0.75 1 1.25 1.5 1.75 2 2.25 2.5 2.75 3 3.25
-1
-2
-3
-4
Distance
(a) Why does the potential energy approach zero as the distance gets bigger?
(b) At what separation distance, in terms of σ and ɛ, is the potential energy zero?
(c) At approximately what distance is the system in equilibrium? What is the potential
energy at that distance? (Express your answers in terms of σ and ɛ.)
(d) How much energy would you need to add to the system at equilibrium in order
to break the molecular bonds holding it together? Why?
(e) How much energy is released in the breaking of those molecular bonds? Why?
Note - no calculation is needed to answer these problems!
————————————————————————————————————
Solution
(a) As the two molecules get further apart, the attractive force between them gets
weaker and weaker. When the are very far apart, they hardly interact at all -
they are basically free molecules. The potential energy of a free particle is zero,
since potential energy depends on the interaction between multiple particles.
1

(b) We can just read the value off from the graph. We see that the potential energy
crosses the x axis when x = 1, which means that r = σ. We can see this from the
equation, too: setting r = σ gives P E(σ) = 0.
(c) The system is in equilibrium when the net force on it is zero. Since the force is
the slope of the potential energy graph, this happens when the slope is zero. The
potential energy graph has zero slope when it’s at it’s minimum point. Checking
the graph, we see that this happens right around x ≈ 1.15, or r ≈ 1.15σ. We could
check the exact answer by finding d
dr (P E(r)) = 0, which gives r = 21/6 σ ≈ 1.12σ,
and so we were close on our guess. The energy at this distance can just be read
off the graph, giving y = −3, or P E = −3ɛ.
(d) In order to break the molecular bonds apart, we’d need to raise the energy to
zero. At equilibrium the energy is P E = −3ɛ, and so we’d need to add +3ɛ units
of energy.
(e) There is no energy released in breaking these molecular bonds - we had to add
the energy to break these bonds. Energy is never released in the breaking of
bonds! One can obtain energy by breaking a less stable bond, then forming a
more stable bond. The more stable bond has a more negative potential energy
(a deeper potential “well”). The difference in energy between the initial and final
states is released to the environment. This is where the energy comes from in the
ATP reactions, and not by releasing energy from the breaking of bonds!
2

2. In a potassium chloride molecule, the distance between the potassium ion (K + ) and
the chloride ion (Cl − ) is 2.80 × 10 −10 m.
(a) Calculate the energy (in Joules and eV) required to separate the two ions to an
infinite distance apart (i.e., to break the bonds holding the molecule together).
(Model the two ions as two point particles initially at rest.)
(b) If twice the energy determined in part (a) is actually supplied, what is the total
amount of kinetic energy that the two ions have when they were an infinite
distance apart?
————————————————————————————————————
Solution
(a) The potential energy of the molecule is just the electrostatic energy,
P E = − 1
4πɛ0
qQ
r ,
where q and Q are the two charges, and r is their separation distance. The net
charge on each ion is ±e, the electron charge. Plugging in the numbers gives
P E = − 1
4πɛ0
qQ
r = −9 × 109 × (1.602 × 10−19 ) 2
2.80 × 10−10 = −8.25 × 10 −19 Joules.
One Joule is 1.602 × 10 −19 eV, so the potential energy in electron volts is P E =
−5.15 eV. This potential energy is the energy released when the two ions bonded,
and to break these bonds we would need to add the exact same amount of energy.
Thus, the energy required to break the bonds and separate the two ions to an
infinite distance is 5.15 electron volts.
(b) The minimum energy needed to break the molecule is 5.15 eV, which just separates
the ions with no final kinetic energy. So, any additional energy put into breaking
the bonds would go into the kinetic energy of the two ions. Thus, if we put in
an extra 5.15 eV of energy, then this will be the total kinetic energy of the ions
when they are infinitely separated.
3

3. Calculate the potential inside and outside a sphere of radius R and charge Q, in which
the the charge is distributed uniformly throughout the sphere. (Hint: recall the electric
fields inside and outside a uniformly charged sphere from Gauss’s law, and don’t forget
that the potentials must be continuous at the surface of the sphere, where r = R.)
————————————————————————————————————
Solution
The electric field outside a uniformly charged sphere is just the ordinary Coulomb law,
Eout = 1
4πɛ0
Q
,
r2 while inside, as we have seen from Gauss’s law, the field is
Ein = 1
4πɛ0
Q
r.
R3 Now, the potential outside the sphere is simply the electrostatic potential of a point
charge,
Vout = 1 Q
4πɛ0 r .
The potential inside the sphere is a bit harder. We can find it by integrating the
electric field, looking for the total work done in bringing in a unit charge from infinity
and placing it at some position inside the sphere. Thus,
r
Vin(r) = −
∞
R r
E · ds = − Eout · ds −
∞
R
Ein · ds,
where we have split up the integral because the electric field is different in the two
regions. So, plugging in the fields and integrating over radial distance, r, gives
Vin(r) = − Q
4πɛ0
R
∞
dr Q
−
r2 4πɛ0R3 r
r dr =
R
1 Q 1
−
4πɛ0 R 4πɛ0
Q
2R3 2 2
r − R .
Simplifying and combining the terms gives our final result for the potential,
Vin(r) = Q
8πɛ0R
Note that Vin(R) = Vout(R), as we require.
4
3 − r2
R 2
.

4. A solid sphere of radius R has a uniform charge density ρ and total charge Q. Derive an
expression for its total electric potential energy in terms of R and Q. (Hint: Imagine
that the sphere is constructed by adding successive layers of concentric shells of charge
dq = (4πr 2 dr) ρ and use dU = V dq.)
————————————————————————————————————
Solution
Suppose that the sphere starts out as a ball of radius r and charge q. Then, the voltage
of the ball is
V (r) = 1 q
4πɛ0 r .
The work required to bring in a tiny charge dq and place it on the surface of the ball
is dU = V dq, or
dU = 1 qdq
4πɛ0 r .
Now, we can’t directly integrate this to get the total potential energy because the
radius doesn’t stay fixed - it builds up to a final radius of R. So, we need to express
the charge in terms of the radius. We know that q = 4π
3 r3 ρ, such that dq = 4πr 2 drρ,
where the charge density is constant. Thus,
dU = 1
4πɛ0
(4π) 2 ρ 2
3
r 4 dr.
Now we can integrate this result, building the radius up from zero to R,
U = 1 (4π)
4πɛ0
2 ρ2 R
r
3 0
4 dr = 1
4πɛ0
(4π) 2 ρ 2 R 5
We can express this result in terms of the total charge Q recalling that ρ = Q/Vol =
3Q
4πR 3 , and so we finally find
U = 1 (4π)
4πɛ0
2 ρ2R5 15
5
= 1
4πɛ0
9Q 2 R 5
15R
15
3 Q
= 6 5
2
4πɛ0R .
.

5. When an uncharged conducting sphere of radius a is placed at the origin of an xyz
coordinate system that lies in an initially uniform electric field E = E0 ˆ k, the resulting
electrostatic potential is V (x, y, z) = V0 for points inside the sphere, and
V (x, y, z) = V0 − E0z +
E0a 3 z
(x 2 + y 2 + z 2 ) 3/2
for points outside the sphere, where V0 is the (constant) electrostatic potential on the
conductor. Use this equation to determine the x, y, and z components of the resulting
electric field. What is the full electric field in vector notation?
————————————————————————————————————
Solution
The electric field may be found from the potential by taking the gradient,
such that the components are Ex = − ∂V
need to take the partial derivatives.
E = −∇V,
So, the x and y components are straightforward,
Ex = − ∂V
∂x = −E0a 3 z ∂
1
∂x
and
Ey = − ∂V
∂y = −E0a 3 z ∂
∂y
∂x , Ey = − ∂V
∂y , and Ez = − ∂V
∂z
(x 2 + y 2 + z 2 ) 3/2
1
(x 2 + y 2 + z 2 ) 3/2
The z component is more work, but not too much more.
Ez = − ∂V
∂
= −
∂z ∂z
V0 − E0z +
E0a3
z
= E0−
(x 2 + y 2 + z 2 ) 3/2
=
=
3E0a 3 zx
(x2 + y2 + z2 , 5/2
)
3E0a 3 zy
(x2 + y2 + z2 . 5/2
)
E0a 3
(x 2 + y 2 + z 2 )
. Thus, we just
3/2 +
3E0a3z2 (x2 + y2 + z2 . 5/2
)
This is all of the components, and we can write the full electric field in component
form as
E = −∇V = − ∂V ∂V
î −
∂x ∂y ˆj − ∂V
∂z ˆ k,
such that
E =
3E0a 3 zx
(x 2 + y 2 + z 2 )
5/2 î+
3E0a 3 zy
(x2 + y2 + z2 ˆj+ 5/2
)
6
E0 −
E0a 3
(x2 + y2 + z2 + 3/2
)
3E0a 3 z 2
(x 2 + y 2 + z 2 ) 5/2
ˆk.