Contact Geometry of second order I - Dept. Math, Hokkaido Univ ...
Contact Geometry of second order I - Dept. Math, Hokkaido Univ ...
Contact Geometry of second order I - Dept. Math, Hokkaido Univ ...
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
⎧ ⎛<br />
0<br />
⎜0<br />
⎪⎨<br />
⎜<br />
⎜0<br />
⎜<br />
⎜ξ<br />
⎜<br />
⎜0<br />
⎝<br />
⎪⎩<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
ξ1<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
−ξ1<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
−<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
tξ 0 0<br />
⎞ <br />
<br />
<br />
⎟ <br />
⎟ <br />
⎟ <br />
⎟ <br />
⎟ ξ ∈ K<br />
⎟ <br />
⎟ <br />
⎠ <br />
<br />
0<br />
<br />
k ⎫<br />
⎪⎬<br />
, ξ1 ∈ K ,<br />
⎪⎭<br />
⎧ ⎛<br />
0<br />
⎜ 0<br />
⎪⎨<br />
⎜<br />
⎜x1<br />
⎜ 0<br />
⎜ 0<br />
⎝<br />
⎪⎩<br />
0<br />
0<br />
0<br />
0<br />
x<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
−<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
t 0 0 0<br />
x<br />
0<br />
0<br />
−x1<br />
0<br />
0<br />
⎞ <br />
<br />
<br />
⎟ <br />
⎟ <br />
⎟ <br />
⎟ <br />
⎟ = ˆx + ˆx1 x ∈ K<br />
⎟ <br />
⎟ <br />
0<br />
⎠ <br />
<br />
0<br />
<br />
k ⎫<br />
⎪⎬<br />
, x1 ∈ K ,<br />
⎪⎭<br />
⎧ ⎛<br />
0<br />
⎜a1<br />
⎪⎨<br />
⎜ 0<br />
⎜ 0<br />
⎜ 0<br />
⎝<br />
⎪⎩<br />
0<br />
0<br />
x0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
a<br />
0<br />
0<br />
0<br />
0<br />
0<br />
−<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
t 0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
a<br />
0<br />
0<br />
0<br />
−x0<br />
0<br />
0<br />
0<br />
−a1<br />
⎞<br />
<br />
<br />
<br />
⎟<br />
<br />
⎟<br />
<br />
⎟<br />
<br />
⎟<br />
<br />
⎟ = ˆx0 + â1 + â <br />
⎟<br />
<br />
0⎟<br />
<br />
0<br />
⎠<br />
<br />
<br />
0<br />
<br />
x0, a1 ∈ K,<br />
a ∈ K k<br />
⎫<br />
⎪⎬<br />
,<br />
⎪⎭<br />
ˇg0<br />
⎧ ⎛<br />
b<br />
⎜0<br />
⎪⎨<br />
⎜<br />
⎜0<br />
⎜<br />
= ⎜0<br />
⎜<br />
⎜0<br />
⎝<br />
⎪⎩<br />
0<br />
0<br />
0<br />
c<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
e<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
B<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
−e<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
0<br />
−c<br />
0<br />
⎞ <br />
⎫<br />
0 <br />
<br />
0 ⎟ <br />
⎟ <br />
0 ⎟ <br />
⎪⎬<br />
⎟ <br />
0 ⎟ b, c, e ∈ K, B ∈ o(k)<br />
⎟ <br />
0 ⎟ <br />
0<br />
⎠ <br />
<br />
⎪⎭<br />
−b<br />
<br />
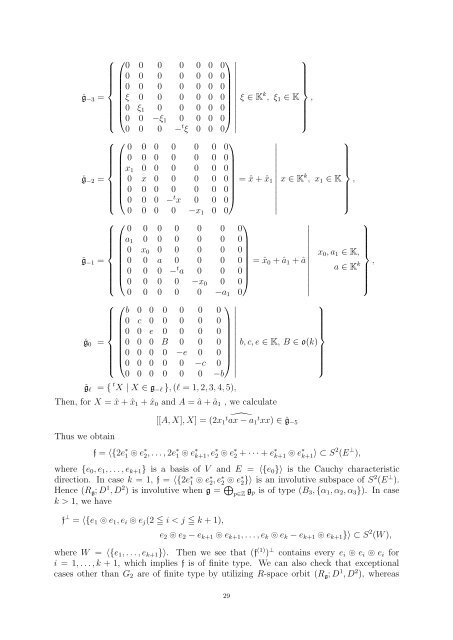
ˇg−3 =<br />
ˇg−2 =<br />
ˇg−1 =<br />
ˇgℓ = { t X | X ∈ g−ℓ }, (ℓ = 1, 2, 3, 4, 5),<br />
Then, for X = ˆx + ˆx1 + ˆx0 and A = â + â1 , we calculate<br />
Thus we obtain<br />
[[A, X], X] =<br />
<br />
(2x1 t ax − a1 t xx) ∈ ˇg−5<br />
f = 〈{2e ∗ 1 ⊚ e ∗ 2, . . . , 2e ∗ 1 ⊚ e ∗ k+1, e ∗ 2 ⊚ e ∗ 2 + · · · + e ∗ k+1 ⊚ e ∗ k+1〉 ⊂ S 2 (E ⊥ ),<br />
where {e0, e1, . . . , ek+1} is a basis <strong>of</strong> V and E = 〈{e0}〉 is the Cauchy characteristic<br />
direction. In case k = 1, f = 〈{2e∗ 1 ⊚ e∗ 2, e∗ 2 ⊚ e∗ 2}〉 is an involutive subspace <strong>of</strong> S2 (E⊥ ).<br />
Hence (Rg; D1 , D2 ) is involutive when g = ⊕<br />
p∈Z gp is <strong>of</strong> type (B3, {α1, α2, α3}). In case<br />
k > 1, we have<br />
f ⊥ = 〈{e1 ⊚ e1, ei ⊚ ej(2 ≦ i < j ≦ k + 1),<br />
e2 ⊚ e2 − ek+1 ⊚ ek+1, . . . , ek ⊚ ek − ek+1 ⊚ ek+1}〉 ⊂ S 2 (W ),<br />
where W = 〈{e1, . . . , ek+1}〉. Then we see that (f (1) ) ⊥ contains every ei ⊚ ei ⊚ ei for<br />
i = 1, . . . , k + 1, which implies f is <strong>of</strong> finite type. We can also check that exceptional<br />
cases other than G2 are <strong>of</strong> finite type by utilizing R-space orbit (Rg; D 1 , D 2 ), whereas<br />
29