Systematic development of coarse-grained polymer models Patrick ...

3.6. Effective Persistence Length 29
best-fit λ
0
2.0
10
Ns
20 30 40
1.8
1.6
1.4
1.2
1.0
λ
20
15
10
5
0
0.0 0.1 0.2
1/ν
0.3
0.8
0.00 0.02 0.04
1/ν
0.06 0.08 0.10
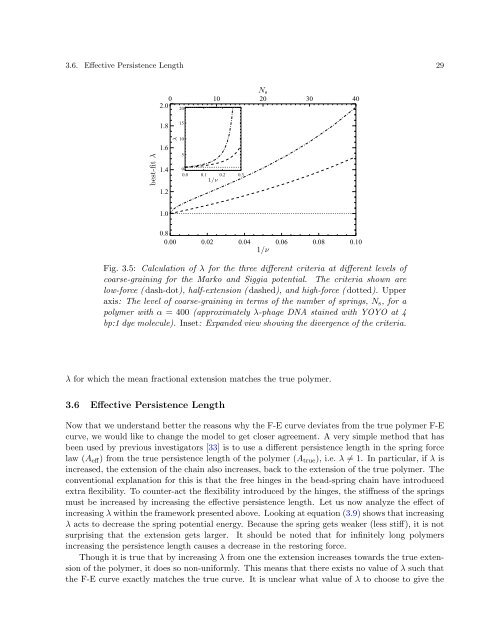
Fig. 3.5: Calculation of λ for the three different criteria at different levels of
coarse-graining for the Marko and Siggia potential. The criteria shown are
low-force ( dash-dot), half-extension ( dashed), and high-force ( dotted). Upper
axis: The level of coarse-graining in terms of the number of springs, Ns, fora
polymer with α = 400 (approximately λ-phage DNA stained with YOYO at 4
bp:1 dye molecule). Inset: Expanded view showing the divergence of the criteria.
λ for which the mean fractional extension matches the true polymer.
3.6 Effective Persistence Length
Now that we understand better the reasons why the F-E curve deviates from the true polymer F-E
curve, we would like to change the model to get closer agreement. A very simple method that has
been used by previous investigators [33] is to use a different persistence length in the spring force
law (Aeff) from the true persistence length of the polymer (Atrue), i.e. λ = 1. In particular, if λ is
increased, the extension of the chain also increases, back to the extension of the true polymer. The
conventional explanation for this is that the free hinges in the bead-spring chain have introduced
extra flexibility. To counter-act the flexibility introduced by the hinges, the stiffness of the springs
must be increased by increasing the effective persistence length. Let us now analyze the effect of
increasing λ within the framework presented above. Looking at equation (3.9) shows that increasing
λ acts to decrease the spring potential energy. Because the spring gets weaker (less stiff), it is not
surprising that the extension gets larger. It should be noted that for infinitely long polymers
increasing the persistence length causes a decrease in the restoring force.
Though it is true that by increasing λ from one the extension increases towards the true extension
of the polymer, it does so non-uniformly. This means that there exists no value of λ such that
the F-E curve exactly matches the true curve. It is unclear what value of λ to choose to give the