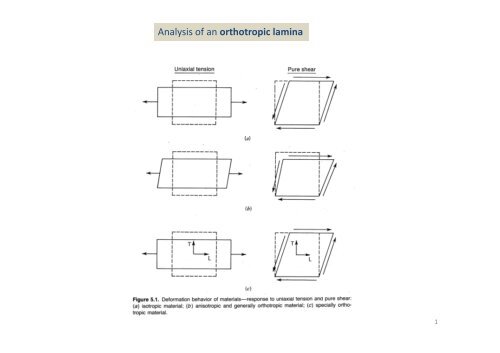
Analysis of an orthotropic lamina

Analysis of an orthotropic lamina
1

Convention
Equilibrium:
Stress tensor
dA 2=dA.n 2
dA 3=dA.n 3
t = n
dA 1=dA.n 1
2

Principal stresses
St Stress invariants: i i t
The principal directions are solutions of
In a coordinate system oriented along the principal directions directions,
the stress tensor is diagonal:
Stress invariants in principal coordinates
3

Generalized Hooke’s law
Because of the symmetry
of the strain tensor
4 th ordertensorof elastic constants
Because of the symmetry
of the stress tensor
Because of the 3 symmetry relationships, the number
of independent elastic constants is reduced
from 3 4 =81 to 21 in the most general anisotropic material
Constitutive
Equation:
The order of partial differentiation
May be changed
4

Change of coordinates in the elastic constants
Let two coordinate systems x and x’ related by the rotation matrix A=a ij
Change g of coordinates of the stress tensor:
Applies to any second order tensor
(same rule for the strain tensor)
5

Tensor of elastic constant:
6

Oth Orthotropic t i composite: it 3 axes of f symmetry t
The elastic constants do not change under coordinate transformations that preserve symmetry
(x ( 1,x 1, 2)plane 2)p
of symmetry
One finds finds:
Similarly, 8 constants must be equal to 0:
Direction cosines:
Must be = 0
7

(x 2,x 3)plane
of symmetry
The following contants
Must also be equal to 0:
Direction cosines:
There is no additional condition coming from the third plane of symmetry (x (x1,xx 3). )
Overall, there are 21‐12= 9 independent elastic constants for an orthotropic material.
8

Orthotropic materials: 9 independent elastic constants
Hooke’s law may be written in matrix form
Vector of engineering g g
Engineering g g
stress components strain components
Stiffness matrix
[the axes 1,2,3 coincide with the natural (orthotropy) axes of the material]
9

In two dimensions:
Stiffness matrix
Compliance matrix
10

Stress‐strain relations and engineering constants for orthotropic lamina
1.
The compliance matrix may be constructed
column by column by considering 3 load cases:
One gets the first column
of the compliance matrix
11

2.
3.
2 nd column of the
Compliance matrix
3rd column of the
CCompliance li matrix i
12

Orthotropic p lamina in natural axes
1. Compliance matrix
For an isotropic lamina,
E L=E T , G=E/2(1+)
2. Stiffness matrix
13

Change of coordinates
For a 2 nd order tensor:
[T] is not a
rotation matrix !!
Change of reference frame
We seek the transformation matrix [T]
14

In L‐T axes:
In arbitrary axes:
Stress‐strain relationship
15

Stiffness matrix in arbitrary axes
16

Compliance matrix in arbitrary axes:
17

Example: find the strains in the lamina =60°
Elastic constants:
Stresses:
Step 11: compute the stresses in orthotropy axes
18

Step 2: compute the strains in natural axes:
19

Step 3: compute the strains in the axes (x,y)
[T(‐] [T( ]
LT
20

Engineering constants
The compliance matrix in
arbitrary bit axes may bbewritten: itt
All the elastic constants may be expressed in
terms of the 4 constants: EL, ET, GLT, LT. 21

Graphite‐epoxy system Boron‐epoxy system
E x < E T
22

Balanced lamina: E T=E L, LT= TL
Not isotropic !!
23