Apr. 20: Hartree-Fock-Bogoliubov, BCS

Hartree-Fock-Bogoliubov
A. Two-body (density-dependent) interaction:
H ˆ = ! t ij
c + i
c j
+ 1 4! v ijkl
c + i
c + j
c l
c k
ij
ijkl
B. Variational principle:
!E["] = 0; E ["] = " ˆ
H "
" " ; E "
[ ] > E 0
C. Trial wave functions: product states
"( )
! K + = u iK
c i + + v iK
c i
i
# = $ ! K
% ; ! K
# = 0
K
❏ HFB - quasiparticles incorporated
into the HF formalism
❏ HFB wave function - the most general
general Bogoliubov
transformation
HFB wave function
is the quasuparticle
vacuum
product wave function consisting of independently
moving quasiparticles (in HF: particles)
❏ Selfconsistent description of coupling between p-h
an p-p channels

HFB - density matrix and pairing tensor
HFB density matrix
HFB pairing tensor
! ij
" # c j + c i
# , $ ij
" # c j
c i
#
ˆ ! = v * v T , $ ˆ = v * u T
ˆ ! 2 % ˆ ! = % $ ˆ $ ˆ
+ , ˆ ! $ ˆ = $ ˆ ˆ !
ˆ ! =
%
'
&
ˆ " # ˆ
$ # ˆ
1 $ ˆ
" *
(
*, ! ˆ 2 = ! ˆ
)
! ˆ % u K(
' * = 0, ! ˆ v *
% (
K
' *
& v K ) & u K )
* = v *
% (
'
K
* *
& u K )
Generalized
density matrix
Eigenvalues are 0 or 1 (thus
defining occupations of
quasiparticle states)
ˆ H (c + ,c) ! ˆ H (" + ,") = E 0
+ ˆ H 20
+ ˆ H 11
+ ˆ H int
Independent quasiparticle
Hamiltonian (H HFB )
[ H ˆ , N ˆ ] = 0, but H ˆ
HFB
, N ˆ
[ ] ! 0
Quasiparticle
interaction
However, we require that ˆ N = N " ˆ H ' = ˆ H # $ ˆ N

HFB equations
ˆ K =
$ h ˆ ! "
&
%
! ˆ # * ! ˆ
h ij
= t ij
+ * ij
# ˆ '
)
h * + "(
* ij
= + v iljk
, kl
kl
# ij
= 1 2 + v ijkl
- kl
kl
HFB Hamiltonian
HF Hamiltonian
Selfconsistent HF field
Selfconsistent pair field
HFB equations
$ h ˆ ! "
&
%
! ˆ # * ! ˆ
# ˆ ' $
) u K'
$ u
& ) = E
K '
h * K & )
+ "(%
v K ( % v K (
[ K ˆ , . ˆ ] = 0
Complicated
eigenvalue problem
❏ HFB equations treat p-h and p-p on the same footing
❏ Δ is a state-dependent field. In general, it depends on
density and has a kinetic term
❏ The generalized density matrix and the HFB Hamiltonian
can be diagonalized simultaneously
❏ Fermi level determined from the particle number
equation
❏ Often it is convenien to express the HFB equations
in the canonical basis

Independent quasiparticle approach
! k + = u k
c k + " v k
c k
! + k
= u k
c + k
+ v k
c k
Bogoliubov-
Valatin
Transformation
phase convention: u k
= u k
> 0,
ε
v k
= "v k
> 0
F
+
{! k
,! j } = 0, ! k+
,! j
+
{! k
,! j } = # ij
$ u 2 k
+ v 2 k
=1
{ } = 0,
( )
0 = BCS = u k
+ v k
c + +
! k
c k
"
# k
0 = 0
0 ! exp A +
A + =
u k
k > 0
v k
k >0
( ) " =
$ c k
+ +
c k
#
1
n!
n= 0
$ A +
( ) n "
BCS wave function is
the quasiparticle
vacuum!
BCS function is a
superposition of
different number of pairs
❏ Important ground-state correlations are included
❏ BCS wave function does not have a sharp particle
number (an intrinsic wave function!)

BCS equations
ˆ H (c + ,c) ! ˆ H (" + ,") = E 0
+ ˆ H 20
+ ˆ H 11
+ ˆ H int
Independent quasiparticle
Hamiltonian (H BCS )
Quasiparticle
interaction
[ H ˆ , N ˆ ] = 0, but H ˆ
BCS
, N ˆ
[ ] ! 0
However, we require that ˆ N = N " ˆ H ' = ˆ H # $ ˆ N
Particle number
equation
Variational method
! 0 ˆ H ' 0 = 0
˜ " k
= " k
+ # v k ki i
v 2 i
$ %
i > 0
!
N = 2v i
2
i > 0
" k
= #! v kk ii
u i
v i
i >0
v 2 k
= 1 $
2
&
%
1 !
˜ " k
˜ " 2 2
k
+ # k
'
)
(
Pairing gap
equation

BCS model
H ˆ
BCS
! + k1
! + k 2
L! + k n
0 = (E 0
+ E k1
+ E k2
+L+ E k n
)! + k 1
! + k 2
L! + kn
0
E k
=
˜ ! 2 2
k
+ " k
Quasiparticle energy
State-independent monopole pairing force:
V ˆ
pair
= !GP ˆ + P ˆ = !G " c + i
c + i
c j
c j
i, j > 0
P ˆ # c + +
" i
c i
v ijkl
= !G$ ji
$ lk
sgn( j)sgn(k)
i> 0
( )
'
% = G" u i
v i
& %)
G
i> 0 ( 2
"
i > 0
1 *
!1, = 0
E i +
❏ Fermi level can be extracted from
experimental binding energies:
❏ Energy gap in even-even nuclei:
❏ High level density in odd systems:
! = dE
dN
E k1
+ E k2
! 2"
E k
! E k0
" ˜ # k 2 + $ 2 ! $
❏ Pairing gap can be extraxted from experimental
odd-even mass differences:
[ ]
! " # 1 (N +
2 E 2) (
g.s .
+ E N) (N +1)
g.s.
# 2E g.s.

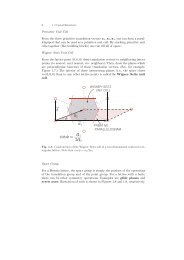
The gap equation
❏ Schematic solution for the case of uniform
density of single-particle states
2
G = ! 1
"1 = G 2
k > 0
E k
b
1
% g (#
)d#
# 2 + $ 2
a
((1/ g G)
If g (#
) & g and Gg

Simple pairing model
+ε
-ε
+ε
+
-ε
Ω times
+ ...
N = 2! particles " # = 0 (assuming Gv 2 < $)
1
G = ! E " % = $
&
(
'
G
G crit
2
)
+
*
,1, G crit
= $ !
Δ
Normal phase
Correlations
beyond BCS
Superconductor
Phase transition
G crit
G
❏ Correlations are important, especially
for small values of G
❏ Static description breaks down when the
single-particle level density is small

Recall that v 2 k is the occupation probability for state k. Thus, the
pairing interaction destabilizes the Fermi surface!
Inserting these results into Eq. (1) yields the Gap Equation
∆ k = − 1 2
∑
v kkll
l>0
∆ k
√˜ε
2
k + ∆ 2 k
This equation, together with the Equation for the energies ˜ε k has to
be solved iteratively.
Simple examples and illustration:
(1) Pure pairing force: v ijkl = −G, t k,l = δ kl ε l
Gap equation
∆ = G 2
∑
l>0
∆
√
(εk − µ) 2 + ∆ 2 k
For vanishing single-particle energies ε k = 0 and a single-j shell one
recovers the results of the seniority model. The gap becomes
√
∆ = G
n √
2
⎛
⎝Ω − N 2
⎞
⎠ = GΩ
2
at half filling. Comparison with the seniority model shows that 2∆ is
the energy to break a pair and equals the excitation energy!

(2) Analytical solution for simple model.
Assume constant interaction G, constant gap ∆, and constant density
of states ρ, and restrict summation to the vicinity δ of the Fermi
surface. Gap equation:
1 = G 2
µ+δ ∫
µ−δ
For weak pairing Gρ ≪ 1 one finds
ρ(ε)
dε√ (ε − µ)2 + ∆ = Gρ arsinh δ 2 ∆
⎛
∆
δ ∝ exp ⎜
−1
⎝
|G|ρ
Gap is nonperturbative in interaction G!
The particle number variance is
(∆N) 2 ≈ 2ρ∆ atan δ ⎧
⎪⎨
∆ = πρ∆ for weak pairing ∆ ≪ δ,
⎪ ⎩ 2ρδ for strong pairing.
⎞
⎟
⎠

BCS essentials
1. The Fermi surface of a Fermi gas is unstable with respect to attractive
interactions. The gap equation has a nontrivial solution
∆ ≠ 0 whenever the interaction or the density of states is sufficiently
large.
2. The finite excitation gap causes superfluidity: The system cannot
absorb arbitrarily small perturbations and therefore remains inert
(See, e.g., Landau & Lifshitz, Statistical Mechanics II).