The Mathematics of Beam Deflection

Questions
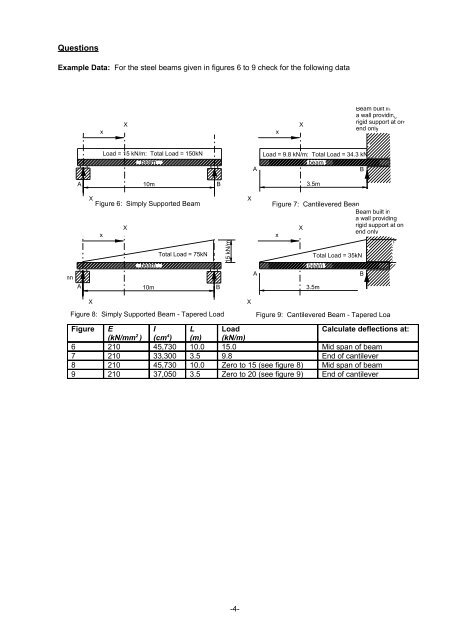
Example Data: For the steel beams given in figures 6 to 9 check for the following data
x
X
x
X
Beam built in to
a wall providing
rigid support at one
end only
Load = 15 kN/m: Total Load = 150kN
beam
A
Load = 9.8 kN/m: Total Load = 34.3 kN
beam
B
A
10m
B
3.5m
X
Figure 6: Simply Supported Beam
X
x
X
Figure 7: Cantilevered Beam
Beam built in to
a wall providing
X
rigid support at one
end only
x
column
A
Total Load = 75kN
beam
10m
B
15 kN/m
A
Total Load = 35kN
beam
3.5m
B
20 kN/m
X
Figure 8: Simply Supported Beam - Tapered Load
X
Figure 9: Cantilevered Beam - Tapered Load
Figure E
I L Load
Calculate deflections at:
(kN/mm 2 ) (cm 4 ) (m) (kN/m)
6 210 45,730 10.0 15.0 Mid span of beam
7 210 33,300 3.5 9.8 End of cantilever
8 210 45,730 10.0 Zero to 15 (see figure 8) Mid span of beam
9 210 37,050 3.5 Zero to 20 (see figure 9) End of cantilever
-4-