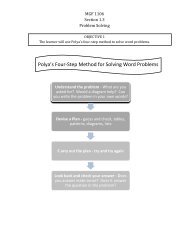
MGF 1107 Section 15.2 Euler Paths and Euler Circuits Puzzle books ...

MGF 1107
Section 15.2 Euler Paths and Euler Circuits
Puzzle books often have a problem that reads “Can you trace this figure without picking up your pencil
and without going over any line twice?” Here are two examples.
We can answer this question by using graph theory.
Objective 1: The learner will determine if a path is an Euler path, an Euler circuit, or neither.
Euler Path – a path that travels through every edge of a graph once and only once. Each graph
must be traveled and no edge can be retraced.
Euler Circuit – a circuit that travels through every edge of a graph once and only once
Notes: Every Euler circuit is an Euler path because an Euler circuit is just an Euler path
that begins and ends at the same vertex.
Every Euler path is not a Euler circuit because an Euler path does not have to end at the
same vertex it started at.
Example 1: Work problems 1 – 3 on page 837.

Objective 2: The learner will use Euler’s Theorem.
Euler’s Theorem:
Number of Odd Vertices in a Connected Graph
(Must be an even number)
Exactly two
•At least one
Euler path but
no Euler circuit
•Each Euler path
must start at
one of the odd
vertices and
end at the
other one
Zero
•At least one
Euler circuit
(which is also
an Euler path)
•It can start and
end at any
vertex.
More than two
•No Euler paths
and No Euler
circuits
Example 2: Given the number of odd and even vertices, determine if the graph has an Euler path
(but no Euler circuits), an Euler circuit, or neither.
a) The graph has 24 even vertices and no odd vertices.
b) The graph has 84 even vertices and two odd vertices.
c) The graph has 55 even vertices and six odd vertices.
Example 3: Explain why the graph in problem 7 on page 837 has at least one Euler path. Use trial
and error to find one such path.
Solution: A (3) – odd, B (3) – odd, C (2) – even, D (4) – even, E (2) even.
The graph has exactly two odd vertices so it has at least one Euler path.
One path : A, C, D, A, B, D, E, B

Example 4: Explain why the graph in problem 10 on page 837 has an Euler circuit. Find one
possible circuit.
A
B
C
D
E
Solution: A (4) – even, B (2) – even, C (4) – even, D(4) – even, E(2) – even
The graph has no odd vertices so it has at least one Euler circuit.
One circuit: A, B, C, E, D, C, A, D, A
Example 5: Work problem 12 on page 837.
Solution: A (2) – even, B(3) – odd, C(3) – odd, D(2) – even, E(3) – odd
We’ve found more than two odd vertices so the graph has no Euler paths and no Euler circuits.

Let’s return to the opening example.
Puzzle books often have a problem that reads “Can you trace this figure without picking up your pencil
and without going over any line twice?” Here are two examples.
Can we answer the question using graph theory?
Objective 3: The learner will solve problems using Euler’s Theorem.
Example 6: Work problems 48, 55 and 56 on pages 839 – 841.