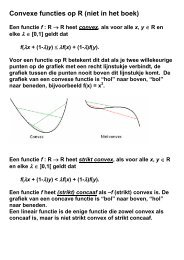
Exercises

Discrete (and Continuous) Optimization
WI4 131
Kees Roos
Technische Universiteit Delft
Faculteit Electrotechniek, Wiskunde en Informatica
Afdeling Informatie, Systemen en Algoritmiek
e-mail: C.Roos@ewi.tudelft.nl
URL: http://www.isa.ewi.tudelft.nl/˜roos
November – December, A.D. 2004

Course Schedule
1. Formulations (18 pages)
2. Optimality, Relaxation, and Bounds (10 pages)
3. Well-solved Problems (13 pages)
4. Matching and Assigments (10 pages)
5. Dynamic Programming (11 pages)
6. Complexity and Problem Reduction (8 pages)
7. Branch and Bound (17 pages)
8. Cutting Plane Algorithms (21 pages)
9. Strong Valid Inequalities (22 pages)
10. Lagrangian Duality (14 pages)
11. Column Generation Algorithms (16 pages)
12. Heuristic Algorithms (15 pages)
13. From Theory to Solutions (20 pages)
Optimization Group 1

Capter 12
Heuristic Algorithms
Optimization Group 2

Exercise 12.7.1
Apply the different heuristics to an instance of STSP with the following distance matrix
⎛
⎜
⎝
- 28 57 72 81 85 80
28 - 28 45 54 57 63
57 28 - 20 3 28 57
72 45 20 - 10 20 72
81 54 3 10 - 22 81
85 57 28 20 22 - 63
80 63 57 72 81 63 -
Pure Greedy Solution: Order the edges according to nondecreasing cost, and seek to use
them in this order.
3
2
1
4 5
7
6
Heuristic tour
#1
step arc length
1 (3,5) 3 accept
2 (4,5) 10 accept
3 (3,4) 20 subtour
4 (4,6) 20 accept
5 (5,6) 22 subtour
6 (1,2) 28 accept
7 (2,3) 28 accept
8 (1,7) 80 forced
9 (6,7) 63 forced
⎞
⎟
⎠
The length of the created tour is z 1 =
3+10+20+28+28+80+63 =
232. The same tour is obtained by using
the insertion heuristic using nearest
neighbor (starting at any node) and farthest
neighbor (starting at node 3, else
the length becomes 251). The tour is
2-optimal.
Optimization Group 3

Exercise 12.7.1 (other heuristic solution)
⎛
⎜
⎝
- 28 57 72 81 85 80
28 - 28 45 54 57 63
57 28 - 20 3 28 57
72 45 20 - 10 20 72
81 54 3 10 - 22 81
85 57 28 20 22 - 63
80 63 57 72 81 63 -
Let us solve the assignment relaxation. We use the same technique as in Exercise 4.5.9. We
first construct a dual feasible solution (since we minimize we invert the weights).
⎞
⎟
⎠
-28 -28 -3 -10 -3 -20 -57
0 - -28 -57 -72 -81 -85 -80
0 -28 - -28 -45 -54 -57 -63
0 -57 -28 - -20 -3 -28 -57
0 -72 -45 -20 - -10 -20 -72
0 -81 -54 -3 -10 - -22 -81
0 -85 -57 -28 -20 -22 - -63
0 -80 -63 -57 -72 -81 -63 -
⇒
-190 -28 -28 -3 -10 -3 -20 -57
0 - 0 -54 -62 -78 -65 -23
0 0 - -25 -35 -51 -37 -6
0 -29 0 - -10 0 -8 0
0 -44 -17 -17 - -7 0 -15
0 -53 -26 0 0 - -2 -24
-6 -51 -23 -19 -4 -13 - 0
-35 -17 0 -19 -27 -43 -8 -
Thus u = (0, 0, 0, 0, 0, −6, −28), v = (−28, −28, −3, −10, −3, −20, −57) is
the initial dual feasible solution and w = −183.
Optimization Group 4

Exercise 12.7.1 (cont.)
-190 -28 -28 -3 -10 -3 -20 -57
0 - 0 -54 -62 -78 -65 -23
0 0 - -25 -35 -51 -37 -6
0 -29 0 - -10 0 -8 0
0 -44 -17 -17 - -7 0 -15
0 -53 -26 0 0 - -2 -24
-6 -51 -23 -19 -4 -13 - 0
-35 -17 0 -19 -27 -43 -8 -
-198 -28 -20 -3 -10 -3 -20 -57
-8 - 0 -46 -54 -70 -57 -15
0 0 - -25 -35 -51 -37 -6
0 -29 -8 - -10 0 -8 0
0 -44 -25 -17 - -7 0 -15
0 -53 -34 0 0 - -2 -24
-6 -51 -31 -19 -4 -13 - 0
-43 -9 0 -11 -19 -35 0 -
-205 -28 -13 -3 -10 -3 -13 -57
-15 - 0 -39 -47 -63 -57 -8
0 0 - -25 -35 -51 -44 -6
0 -29 -15 - -10 0 -15 0
-7 -37 -25 -10 - 0 0 -8
0 -53 -41 0 0 - -9 -24
-6 -51 -38 -19 -4 -13 - 0
-50 -2 0 -4 -12 -28 0 -
*
7
6
7’
6’
⇒
*
7
6
7’
6’ *
⇒
*
*
7
6
7’ *
6’ *
5
5’
5
5’
5
5’ *
4
4’
*
4
4’
*
4
4’
3
3’
3
3’
*
3
3’
2
2’ *
2
2’ *
2
2’ *
*
1
1’
*
1
1’
*
1
1’
δ = 8
δ = 7
δ = 2
Optimization Group 5

Exercise 12.7.1 (cont.)
-205 -28 -13 -3 -10 -3 -13 -57
-15 - 0 -39 -47 -63 -57 -8
0 0 - -25 -35 -51 -44 -6
0 -29 -15 - -10 0 -15 0
-7 -37 -25 -10 - 0 0 -8
0 -53 -41 0 0 - -9 -24
-6 -51 -38 -19 -4 -13 - 0
-50 -2 0 -4 -12 -28 0 -
-207 -28 -11 -3 -10 -1 -11 -55
-17 - 0 -37 -45 -63 -57 -8
0 0 - -25 -35 -53 -46 -8
-2 -27 -15 - -8 0 -15 0
-9 -35 -25 -8 - 0 0 -8
0 -53 -43 0 0 - -11 -26
-8 -49 -38 -17 -2 -13 - 0
-52 0 0 -2 -10 -28 0 -
-209 -28 -11 -1 -8 -1 -11 -55
-19 - 0 -35 -43 -63 -57 -8
-2 0 - -23 -33 -53 -46 -8
-4 -27 -15 - -6 0 -15 0
-11 -35 -25 -6 - 0 0 -8
0 -55 -45 0 0 - -13 -28
-10 -49 -38 -15 0 -13 - 0
-54 0 0 0 -8 -28 0 -
*
*
7
6
7’ *
6’ *
⇒
*
*
7
6
7’ *
6’ *
⇒
*
*
7
6
7’ *
6’ *
5
5’ *
5
5’ *
5
5’ *
*
4
4’
*
4
4’
*
4
4’
*
3
3’
*
3
3’
*
3
3’ *
2
2’ *
*
2
2’ *
*
2
2’ *
*
1
1’
*
1
1’ *
*
1
1’ *
δ = 2
δ = 2
Optimization Group 6

Exercise 12.7.1 (cont.)
-209 -28 -11 -1 -8 -1 -11 -55
-19 - 0 -35 -43 -63 -57 -8
-2 0 - -23 -33 -53 -46 -8
-4 -27 -15 - -6 0 -15 0
-11 -35 -25 -6 - 0 0 -8
0 -55 -45 0 0 - -13 -28
-10 -49 -38 -15 0 -13 - 0
-54 0 0 0 -8 -28 0 -
7
6
5
4
3
2
1
7’
6’
5’
4’
3’
2’
1’
Optimal matching. Length
209.
The optimal matching yields two sub tours: 1 → 2 → 1
and 3 → 5 → 4 → 6 → 7 → 3, with lengths
28+28 = 56 and 3+10+20+63+57 = 153,
respectively. This is a lower bound for an optimal tour.
A heuristic approach might be the following: open the
subtours by removing one edge from each of them and
combine the two pieces to a tour by adding two edges (in
one of the two possible ways). E.g., removing one edge
{1,2} from the first subroute and edge {3,7} form the
second, and adding the edges {1,7} and {2,3} we get
the tour 3 → 5 → 4 → 6 → 7 → 1 → 2 → 3 which
has length 209 − 28 − 57 + 80 + 28 = 232. This
is exactly the same 2-optimal tour that we have found
earlier by using the insertion heuristic.
Optimization Group 7

Exercise 12.7.2
Apply greedy and local neighborhood heuristics to an instance of the problem of most profitably
allocating clients to at most K depots with m = 7 clients, n = 6 potential depots, K = 3,
and the following cost matrix:
(c ij ) =
⎛
⎜
⎝
2 3 7 3 6 1
3 1 1 8 10 4
6 2 3 1 2 7
8 1 4 6 2 3
4 4 3 3 4 3
2 8 3 6 3 2
6 5 3 2 7 4
The column sums in the cost matrix are respectively 31,24,24,29,34 and 24. So from
a greedy point of view the depots 2, 3 and 6 are most profitable. Let us start our greedy
solution with S = {2}. We choose the second depot from the other depots so as to minimize
the cost. When adding depot 1 the cost becomes 2+1+2+1+4+2+5 = 17. When
adding the other (single) depots these costs become 16 for depot 3, 17 for depot 4, 19 for
depot 5 and 14 for depot 6. So our new solution is S = {2,6}, with cost 14. Adding a
third depot to this set the costs become 14 for depot 1, 13 for depot 3, 11 for depot 4 and
14 for depot 5. Thus we choose to add depot 4, which gives S = {2,4,6}, with cost 11.
⎞
⎟
⎠
Optimization Group 8

Exercise 12.7.2 (cont.)
(c ij ) =
⎛
⎜
⎝
2 3 7 3 6 1
3 1 1 8 10 4
6 2 3 1 2 7
8 1 4 6 2 3
4 4 3 3 4 3
2 8 3 6 3 2
6 5 3 2 7 4
We found the greedy solution S = {2,4,6}, with cost 11. Let us apply a local search to
this solution. Since the number of depots is fixed (K = 3), a natural neighborhood consists
of all sets T arising by replacing one depot in S by a depot not belonging to S:
T cost(T)
{1,4,6} 15
{3,4,6} 13
{4,5,6} 15
{1,2,6} 14
{2,3,6} 13
{2,5,6} 14
{1,2,4} 12
{2,3,4} 14
{2,4,5} 14
It is clear from this table that S is locally optimal.
⎞
⎟
⎠
Optimization Group 9

Exercise 12.7.3
Devise a greedy heuristic for the set covering problem.
Solution: The set covering problem is given by
min
⎧
⎨
∑
⎩
j∈N
c j x j :
∑
j∈N
a ij x j ≥ 1 for i ∈ M, x ∈ {0,1} n ⎫
⎬
⎭ ,
where N = {1, . . . , n}, M = {1, . . . , m}, and a ij ∈ {0,1} for i ∈ M and j ∈ N.
Let s j be the 0-1 vector consisting of all a ij ’s, i ∈ M and S j the subset of M which has
s j as incidence vector. If x j = 1, then all constraints ∑ j∈N a ij x j ≥ 1 with i ∈ S j are
satisfied. In other words, if x j = 1 then all elements of the subset S j of M are covered.
The contribution to the cost function is c j . The cost per covered element is c j
. So we start
by putting x j = 1 for the (or an) index j that minimizes
c j
|S j |
|S j |
. Without loss of generality
we assume that j = 1. Since the elements in S 1 are now covered, we replace each S j with
j ≥ 2 by Sj 1 = S c
j \ S 1 , and put x j = 1 for the (or an) index j ≥ 2 that minimizes j
Without loss of generality we assume that j = 2. Then we replace each S j with j ≥ 3 by
Sj 2 = S1 j \ S c
2, and put x j = 1 for the (or an) index j ≥ 2 that minimizes j ∣, and so on.
We proceed until all elements of M are covered, and put x j = 0 for the remaining variables.
∣
∣S 2 j
∣
∣
∣S 1 j
Optimization Group 10
.
∣

Exercise 12.7.4
Consider the problem of finding a maximum cardinality matching in a graph G = (V, E). A
mtching M ⊆ E is called maximal if M ∪ {e} is not a matching for any e ∈ E \ M. Let
z be the size of a maximum matching and z H the size of a maximal matching. Show that
z H ≥ 1 2 z.
1
2
3
4
5
6
1’
2’
3’
4’
5’
6’
Example of a
maximal matching.
Solution: Let M be a maximum cardinality matching in G.
Then |M| = z. We know that the size of a maximum cardinality
matching is equal to the minimal size of a covering of the edges
by nodes. So any covering of the edges by nodes contains at least
z nodes.
Now consider the end points of the edges in a maximal matching
M ′ . These points necessarily cover all the edges in G; because
any not covered edge e could be used to extend M ′ to a matching
M ′ ∪ {e}, which is impossible since M ′ is maximal. Hence, the
end points form a covering of the edges by nodes. The number of
the end points being 2 ∣∣ M ′∣ ∣, we have 2 ∣∣ M ′∣∣ ≥ z, which implies
the desired inequality.
Optimization Group 11

Consider the 0-1 knapsack problem:
⎧
⎨
z = max
⎩
Exercise 12.7.5
n∑
c j x j :
j=1
⎫
n∑
⎬
a j x j ≤ b, x ∈ {0,1} n ⎭
j=1
with 0 < a j ≤ b for j ∈ N = {1, . . . , n}. Consider a greedy heuristic that chooses the better of the integer
round down of the linear relaxation solution and the best solution in which just one variable is set to 1. Show
that z G ≥ 1 2 z.
Solution: Without loss of generality we assume that the variables are ordered such that c j
a j
is non-increasing.
Let r be the largest index such that ∑ r
j=1 a j ≤ b. Then the solution of the linear relaxation is given by
x 1 = . . . = x r = 1, x r+1 = b − ∑ r
j=1 a j
, x r+2 = . . . = x n = 0
a r+1
whence integer round down of the linear relaxation solution yields the solution x 1 with
r∑
x 1 1 = . . . = x 1 r = 1, x 1 r+1 = . . . = x1 n = 0, z 1 = c T x 1 = c j .
The best solution x 2 in which just one variable is set to 1 chooses the index k such that c k ≥ c j for all j and
takes x 2 k = 1 and x2 j = 0 for j ≠ k, with value z2 = c k . Note that the value of the linear relaxation solution
provides an upper bouns for z. Hence, using b − ∑ r
j=1 a j < a r+1 , we may write
z ≤ ¯z =
r∑
j=1
c j + c r+1
b − ∑ r
j=1 a j
a r+1
proving the desired inequality.
≤
r∑
c j + c r+1 ≤
j=1
j=1
⎛
r∑
c j + c k ≤ 2max ⎝
j=1
r∑
j=1
c j , c k
⎞
⎠ = 2z G ,
Optimization Group 12
•