Full-Newton step polynomial-time methods for LO based on locally ...

<strong>Full</strong>­<strong>Newton</strong> <strong>step</strong> <strong>polynomial</strong>­<strong>time</strong> <strong>methods</strong> <strong>for</strong> <strong>LO</strong><strong>based</strong> on locally self­concordant barrier functions(work in progress)Kees Roos and Hossein Mansourie-mail: [C.Roos,H.Mansouri]@ewi.tudelft.nlURL: http://www.isa.ewi.tudelft.nl/∼roosGeorgia Tech, Atlanta, GANovember 21, A.D. 20051

• Self-concordant (barrier) functionsOutline– Definitions– <strong>Newton</strong> <strong>step</strong> and proximity measure– Algorithm with full <strong>Newton</strong> <strong>step</strong>s– Complexity analysis– Minimization of a linear function over a convex domain– Algorithm with full <strong>Newton</strong> <strong>step</strong>s– Complexity analysis• Kernel-function-<strong>based</strong> approach– Linear optimization via self-dual embedding– Central path of self-dual problem– Kernel-function-<strong>based</strong> barrier functions– Complexity results• Local self-concordancy of kernel-function-<strong>based</strong> barrier functions• Analysis of the full <strong>Newton</strong> <strong>step</strong> method• Concluding remarks• Some references2

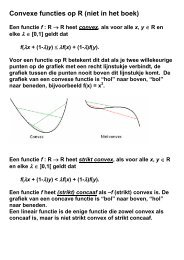
Self-concordant univariate functionsWe start by considering a univariate function φ : D → R. The domain D of the function φmust be an open interval in R. One calls φ a κ-self-concordant (SC) function if there existsa nonnegative number κ such that∣∣∣φ ′′′ (x) ∣ ≤ 2κ ( φ ′′ (x) )32 , ∀x ∈ D. (1)Note that this definition assumes that φ ′′ (x) is nonnegative, whence φ is convex, and moreoverthat φ is three <strong>time</strong>s differentiable.Moreover, if φ ′′ (x) > 0 <strong>for</strong> all x ∈ D, then φ is SC if and only ifis bounded above (by 4κ 2 ).φ ′′′ (x) 2φ ′′ (x) 33

Self-concordant (multivariate) functionsLet φ : D → R be a strictly convex function, where the domain D is an open convex subsetof R n , with n > 1. So φ is a multivariate function.Then φ is called a κ-SC function if its restriction to an arbitrary line in its domain is κ-SC.In other words, φ is a κ-SC if and only if ¯φ(t) = φ(x + th) is κ-SC <strong>for</strong> all x ∈ D and <strong>for</strong>all h ∈ R n . The domain of ¯φ(t) is defined in the natural way: given x and h it consists ofall t such that x + th ∈ D.We want to find the minimal value φ on its domain (if it exists) by <strong>Newton</strong>’s method.4

<strong>Newton</strong> <strong>step</strong> and proximity measureLet φ : D → R be a a strictly convex κ-SC function having a minimizer, and such that theminimal value equals 0. The <strong>Newton</strong> <strong>step</strong> at x is defined by∆x = −H(x) −1 g(x), (2)where g(x) and H(x) denote the gradient and the Hessian of φ(x) at x, respectively. Inthe sequel we always assume that φ is strictly convex. As a consequence, the quantity√√λ(x) = ∆x T H(x)∆x = ‖∆x‖ H(x) = g(x) T H(x) −1 g(x),can be used as a measure <strong>for</strong> the ‘distance’ of x to the minimizer of φ(x).The quantity λ(x) plays a crucial role in the analysis of <strong>Newton</strong>’s method. Many results canbe nicely expressed by using the univariate (nonnegative) function ω(t) defined byFor example, if λ(x) < 1 κthen one hasω(t) = t − ln(1 + t), t > −1. (3)κλ(x) + ln(1 − κλ(x))φ(x) ≤ −Hence, since ω(t) is monotonically decreasing if t ∈ (−1,0], we obtainλ(x) ≤ 1 4κκ 2= ω (−κλ(x))κ 2 .⇒ φ(x) ≤ ω(−1 4 )κ 2 = 0.0376821κ 2 ≤ 126κ 2. 5

Quadratic convergence resultA major result in the theory of self-concordant functions states that the <strong>Newton</strong> process isquadratically convergent if 3κλ(x) < 1. This is because of the following result.Lemma 1 If κλ(x) < 1 then x + ∆x ∈ D and(λ(x)) 2.λ(x + ∆x) ≤ κ1 − κλ(x)Corollary 1 If 3κλ(x) < 1 then x + ∆x ∈ D andλ(x + ∆x) ≤ ( 32λ(x) √ κ ) 2.6

Algorithm with full <strong>Newton</strong> <strong>step</strong>sAssuming that we know a point x ∈ D with λ(x) ≤3κ 1 we can easily obtain a point x ∈ Dsuch that λ(x) ≤ ǫ, <strong>for</strong> prescribed ǫ > 0, with the following algorithm.Input:An accuracy parameter ǫ ∈ (0,1);x ∈ D such that λ(x) ≤ 1 3κ .while λ(x) ≤ ǫ dox := x + ∆xendwhileTheorem 1 Let x ∈ D and λ(x) ≤3κ 1 . Then the algorithm with full <strong>Newton</strong> <strong>step</strong>s requiresat most⎡⎢ log 2⎛⎝ log ǫlog 3 4⎞⎤⌈⎠≤ ⎥(log 2 3.5log 1 ǫiterations. The output is a point x ∈ D such that λ(x) ≤ ǫ.)⌉7

Minimization of a linear function over a convex domainWe consider the problem of minimizing a linear function over a closed convex domain ¯D:(P) min { c T x : x ∈ ¯D } .We assume that we have a self-concordant barrier function φ : D → R, where D = int ¯D,and also that H(x) = ∇ 2 φ(x) is positive definite <strong>for</strong> every x ∈ D. For µ > 0 we defineφ µ (x) := cT xµ+ φ(x), x ∈ D.(P µ ) inf {φ µ (x) : x ∈ D} .We haveg µ (x) := ∇φ µ (x) = c µ + ∇φ(x) = c µ + g(x)H µ (x) := ∇ 2 φ µ (x) = ∇ 2 φ(x) = H(x), ∇ 3 φ µ (x) = ∇ 3 φ(x).Note that the two higher derivatives do not depend on µ. It follows that φ µ (x) is selfconcordant.The minimizer of φ µ (x), if it exists, is denoted as x(µ). When µ runs thoughall positive numbers then x(µ) runs through the central path of (P). We expect that x(µ)converges to an optimal solution of (P) when µ approaches 0. There<strong>for</strong>e we are goingto follow the central path. This approach is likely to be feasible because since φ µ (x) isself-concordant, its minimizer can be computed efficiently.8

<strong>Newton</strong> <strong>step</strong> and proximity measureφ µ (x) := cT xµ+ φ(x), x ∈ D.g µ (x) := ∇φ µ (x) = c µ + ∇φ(x) = c µ + g(x)H µ (x) := ∇ 2 φ µ (x) = ∇ 2 φ(x) = H(x), ∇ 3 φ µ (x) = ∇ 3 φ(x).The <strong>Newton</strong> <strong>step</strong> at x is now given by∆x = −H(x) −1 g µ (x)and the distance of x ∈ D to the µ-center x(µ) is measured by the quantity√λ µ (x) = ∆x T √H(x)∆x = g µ (x) T H(x) −1 g µ (x) = ‖g µ (x)‖ H −1 .9

Effect of a µ-update and the barrier parameter νLet λ = λ µ (x) and µ + = (1 − θ)µ. Our aim is to estimate λ µ +(x). We haveg µ +(x) = cµ + ∇φ(x) = c+ (1 − θ)µ + ∇φ(x)( )cµ + ∇φ(x) − θ∇φ(x)= 11−θHence, denoting H(x) shortly as H,λ µ +(x) = 11−θ ‖g µ(x) − θ∇φ(x)‖ H −1 ≤ 11−θ⎛⎜= 11−θ (g µ(x) − θ∇φ(x)) .⎝ ‖g µ(x)‖ H −1} {{ }λ µ (x)+θ ‖g(x)‖ H −1Definition 1 Let ν ≥ 0. The self-concordant barrier function φ is called a ν-barrier ifλ(x) 2 = ‖g(x)‖ 2 H −1 ≤ ν, ∀x ∈ D.⎞⎟⎠ .An immediate consequence of this definition isLemma 2 If φ is a self-concordant ν-barrier then λ µ +(x) ≤ λ µ(x)+θ √ ν1−θ.10

Input:Algorithm with full <strong>Newton</strong> <strong>step</strong>sAn accuracy parameter ǫ > 0;proximity parameter τ > 0;update parameter θ, 0 < θ < 1;x = x 0 ∈ D and µ = µ 0 > 0 such that λ µ (x) ≤ τ < 1 κ .(while µ ν + τ (τ+ √ ν)1−κτµ := (1 − θ)µ;x := x + ∆x;endwhile)≥ ǫ doTheorem 2 If τ =9κ 1 and θ = 5requires not more than⌈9+36κ √ ν2 ( 1 + 4κ √ ν ) ln 2µ0 νǫ, then the algorithm with full <strong>Newton</strong> <strong>step</strong>siterations. The output is a point x ∈ D such that c T x ≤ c T x ∗ + ǫ, where x ∗ denotes anoptimal solution of (P).⌉11

Graphical illustration of full-<strong>Newton</strong>-<strong>step</strong> path-following methodz 0µecentral pathλ(x) ≤ τz k = x k s k(1 − θ)µez 1One iteration.12

Relevant part of the analysis of the algorithmAt the start of the first iteration we have x ∈ D and µ = µ 0 such that λ µ (x) ≤ τ. When the barrier parameteris updated to µ + = (1 − θ)µ, Lemma 2 givesλ µ +(x) ≤ λ µ(x) + θ √ ν1 − θ≤ τ + θ√ ν1 − θ . (4)Then after the <strong>Newton</strong> <strong>step</strong>, the new iterate is x + = x + ∆x and( ) 2λ µ +(x + λµ +(x)) ≤ κ. (5)1 − κλ µ +(x)The algorithm is well defined if we choose τ and θ such that λ µ +(x + ) ≤ τ. To get the lowest iteration bound,we need at the same <strong>time</strong> to maximize θ. From (5) we deduce that λ µ +(x + ) ≤ τ certainly holds ifλ µ +(x)1 − κλ µ +(x) ≤ √ τ√ κ,which is equivalent to λ µ +(x) ≤the following condition on θ:√ τκ √ τ+ √ κ . According to (4) this will hold if τ+θ√ ν1−θθ ≤ √ τ1 − κτ − √ κτ√ τ +√ νκ( 1 +√ κτ)≤√ τκ √ τ+ √ . This leads toκWe choose τ = 1 9κ . The upper bound <strong>for</strong> θ gets the value 59+36κ √ ν ≤ 12+8κ √ ν , and then λ µ+(x) ≤ 1 4κ .This justifies the choice of the value of τ and θ in the theorem. For the rest of the proof we refer to the relevantreferences.13

Linear optimization via self-dual embedding (1)It is now well known that every linear optimization problem can be solved efficiently if we canfind in <strong>polynomial</strong> <strong>time</strong> a strictly complementary solution of problems of the <strong>for</strong>m(SP) min{q T x : Mx + q ≥ 0, x ≥ 0},where the n ×n matrix M is skew-symmetric (i.e., M T = −M) and q = (0; . . .;0; n) ∈R n , and under the assumption that the all-one vector 1 is feasible with M 1 + q = 1.The problem (SP) is trivial in the sense that it has a trivial optimal solution, namely x = 0,with 0 as optimal value. But this observation is not sufficient <strong>for</strong> our goal, since we need astrictly complementary solution of (SP). What this means requires some explanation.14

Linear optimization via self-dual embedding (2)We associate to any vector x ∈ R n its slack vector s(x) according tos(x) = Mx + q.In the sequel we simply denote s(x) as s, and s will always have this meaning. Since M isskew-symmetric we have z T Mz = 0 <strong>for</strong> every vector z ∈ R n . Hence we haveq T x = (s − Mx) T x = s T x − x T Mx = s T x.There<strong>for</strong>e, if x is feasible, then x is optimal if and only if s T x = 0. Since x and s arenonnegative this holds if and only if x i s i = 0 <strong>for</strong> each i. This shows that x is optimalif and only if the vectors x and s are complementary vectors. We say that x is a strictlycomplementary solution if moreover x i + s i > 0 <strong>for</strong> each i.Summarizing these facts, we have that x is feasible if x ≥ 0 and s ≥ 0. A feasible x isoptimal if xs = 0, and x is a strictly complementary solution if moreover x + s > 0. Thuswe need to solve the systems = Mx + q, x ≥ 0, s ≥ 0,xs = 0x + s > 0.15

Central pathThe basic idea of IPMs is to replace the so-called complementarity condition xs = 0 <strong>for</strong>(SP), by the parameterized equation xs = µ1, with µ > 0. Thus we consider the systems = Mx + q, x ≥ 0, s ≥ 0,xs = µ1.Clearly, any solution (x, s) will satisfy x > 0 and s > 0. Note that x = s = 1 and µ = 1satisfy this system.Surprisingly enough, a solution exists <strong>for</strong> each µ > 0, and this solution is unique. It isdenoted as (x(µ), s(µ)) and we call x(µ) the µ-center of (SP); s(µ) is the correspondingslack vector. The set of µ-centers (with µ running through all positive real numbers) givesa homotopy path, which is called the central path of (SP). If µ → 0 then the limit ofthe central path exists and since the limit point satisfies the complementarity condition, thelimit yields an optimal solution <strong>for</strong> (SP). Moreover, this solution can be shown to be strictlycomplementary.We will start our method at x = s = 1 and µ = 1. The method uses nonnegative barrierfunctions φ µ (x, s), <strong>for</strong> each µ > 0, such that φ µ (x(µ), s(µ)) = 0. If s = Mx + q thenwe denote φ µ (x, s) as Φ µ (x).16

Kernel-function-<strong>based</strong> barrier functionsFirst we choose a kernel function ψ : (0, ∞) → [0, ∞). We require that ψ(t) is three<strong>time</strong>s differentiable and strictly convex, and moreover that ψ(t) is minimal at t = 1, whereasψ(1) = 0. Then we define√ n∑xsΦ µ (x) := φ µ (x, s) = 2 ψ (v i ) where v := , s = Mx + q.µi=1The barrier function Φ µ (x) <strong>based</strong> on the kernel function ψ(t) is defined on the interior ofthe domain of (SP).φ µ (x, s) is strictly convex and minimal when v = 1, and then x = x(µ) (and s = s(µ)).Provided that θ is small enough, after a full <strong>Newton</strong> <strong>step</strong> we get a good enough approximationof x = x(µ). Then we repeat the above process: reduce µ by the factor 1 − θ, do a full<strong>Newton</strong> <strong>step</strong>, etc., until µ is close enough to zero. At the end this yields an ǫ-solution of theproblem (SP).In earlier papers we used a search direction determined by the systemM∆x = ∆s,s∆x + x∆s = −µ v ψ ′ (v).17

Complexity resultsi kernel function ψ i (t) small-update large-update ref.t12 −12 − ln t O ( √ ) n lnnO ( )n ln n RTVǫǫ( )122 t −1 2O ( √ ) ( )tn lnnO n 2 3 ln n PRTǫǫt32 −12 + t1−q −1q−1 , q > 1 O ( q 2√ ) )n ln n O(qn q+12qln n PRTǫǫt42 −12 + t1−q −1q(q−1) − q−1q (t − 1), q > 1 O ( q √ n ) )ln n O(qn q+12qln n PRTǫ ǫ56t 2 −12 + e1 t −eet 2 −12 − ∫ t −1 1 e1 ξdξ O ( √ n lnnǫO ( √ ) n lnnO ( √ǫ n ln 2 n ) ln n BERǫ)O ( √ n ln 2 n ) ln n BERǫ7 t − 1 + t1−q −1q−1 , q > 1 O ( q 2√ n ) ln n ǫO(qn) ln n ǫBRIn all cases the iteration bound <strong>for</strong> small-update <strong>methods</strong> is O ( √ n lognǫ).The best bound <strong>for</strong> large-update <strong>methods</strong> is obtained <strong>for</strong> i ∈ {3,4} by taking q = 1 2log n.This gives the iteration bound O ( √ )n(log n)lognǫ, which is currently the best knownbound <strong>for</strong> large-update <strong>methods</strong>.18

Local self-concordancy of the barrier functionWe define φ : D → R to be locally κ-SC at x ∈ D ⊆ R n if φ(x + th) is κ-SC <strong>for</strong> allh ∈ R n ; to express the dependence of κ on x we use the notation κ(x). Clearly φ is κ-SCif and only if κ(x) is bounded above by some (finite) constant on the domain of φ.It is well known that the classical logarithmic barrier function—whose kernel function is t2 −12 −ln t—is SC. But this is quite exceptional. In general kernel-function-<strong>based</strong> barrier functionsare not SC, but they are locally SC. The following table shows this <strong>for</strong> the kernel function,ψ 2 (t).iteration boundslocal value of κi kernel function ψ i (t) small-update large-update ψ(t) Φ µ (x)1t 2 −12 − ln t O ( √ ) ( )n lnnǫO n lnnǫ1 1( )2 t −1 2tO ( √ )n lnnǫ?122t √32‖v‖ ∞√3At the start of the algorithm we have v = 1, where the local value of κ is 2/ √ 3. Duringthe course of the algorithm the iterates stay so close to the central path that v stays in a verysmall neighborhood of 1, and hence the barrier function is SC <strong>for</strong> some suitable value of κ,slightly larger than 2/ √ 3.19

Assumptions on the kernel functionWe assume thatand we make the following assumptions:ψ(t) = 1 2(t 2 − 1 ) + ψ b (t) (6)ψ b ′ (t) < 0, ψ′′b (t) > 0, ψ′′′b (t) < 0, t > 0.It will be convenient to use the following notations (<strong>for</strong> t > 0):ξ(t) := ψ ′′ (t) − ψ′ (t)t, ξ b (t) = ψ ′′b (t) − ψ′ b (t)t. (7)Note that these definitions implyξ(t) = ξ b (t) > 0, t > 0.20

Consequences of the assumptionFor x > 0 and s > 0 we haveφ µ (x, s) = 2n∑i=1Hence, if s := s(x) = Mx + q thenΦ µ (x) = φ µ (x, s) = xT s − nµµψ (v i ) =+2n∑j=1n∑i=1(v2i − 1 ) + 2n∑i=1ψ b(vj)=q T x − nµµψ b (v i ) .+2n∑j=1ψ b(√xj s jµ).In the special case that ψ(t) is the kernel function of the logarithmic barrier function we haveψ b (t) = −ln t, whenceφ µ (x, s) = qT xµ − n ∑j=1ln ( x j s j)+ nln µ − n,which is (up to the ’constant’ term nln µ − n) the classical primal-dual logarithmic barrierfunction.21

Results on local self-concordancy (1)LetN(t) = √−ψ′ b (t) t > 0.(t),ψ ′′bTheorem 3 ν(x, s) = 2 ‖N(v)‖ 2 .It is quite surprising that the local value of ν depends only on the vector v. Recall that ifx ≈ x(µ) and s ≈ s(µ) then v ≈ 1.We give two examples.i ψ i (t) ψ b (t) ψ ′ b1 t2 −12 1 2(t) ψ′′b2 − ln t −ln t −1 t( )t −1 2 ( 12tt −2 − 1 ) −1 3t 3 t 4(t) ψ′′′b(t) ν(t) ν(v)1t 2 − 2 t 3 2 2n−12t 52t −232‖v −1 ‖ 2322

Proof of Theorem 3We apply the composition rule, which is well known.Lemma 3 Let φ i be (κ i , ν i )-SCB’s on D i , <strong>for</strong> i = 1,2. Then φ 1 + φ 2 is a (κ, ν)-SCB<strong>for</strong> D 1 × D 2 , where κ = max {κ 1 , κ 2 } and ν = ν 1 + ν 2 .Since the linear part in φ µ (x, s) is 0-self-concordant, with ν = 0, it suffices to considerf(x, s) = 2n∑j=1ψ b(√xj s jµwhere s = s(x) = Mx + q. In the sequel we will neglect this relation between s and x.Thus we will prove that f(x, s) is (κ, ν)-self-concordant on the set{(x, s) : x ∈ Rn+ , s ∈ R n }+ .),This will imply that f(x, s) is a (κ, ν)-self-concordant barrier function <strong>for</strong> the domain of(SP), which is the intersection of this set and affine space determined by s = Mx + q.We do this by considering each of the terms in the definition separately and then apply thecomposition rules of Lemma 3.23

The case n = 1 (1)(√ )xsf(x, s) = 2ψ b , x > 0, s > 0.µNow let σ, τ ∈ R and α such that x + ασ > 0 and s + ατ > 0. We defineandWritingv =√ √xs (x + ασ)(s + ατ)µ , v(α) = ,µϕ(α) = f(x + ασ, s + ατ) = 2h = σ x ,k = τ sn∑j=1ψ b (v(α)) .we have, using xs = µv 2 ,(x + ασ)(s + ατ) = xs(1 + αh)(1 + αk) = µv 2 (1 + αh)(1 + αk) ,and hencev(α) 2 = v 2 (1 + αh)(1 + αk) .24

The case n = 1 (2)v(α) 2 = v 2 (1 + αh)(1 + αk) .Taking successive derivatives with respect to α at both sides we obtain2v(α)v ′ (α) = v 2 (h(1 + αk) + k(1 + αh))v(α)v ′′ (α) + v ′ (α) 2 = v 2 hkv(α)v ′′′ (α) + 3 v ′ (α)v ′′ (α) = 0.Substitution of α = 0 givesThis givesv(0) 2 = v 22v ′ (0) = v (h + k)vv ′′ (0) + v ′ (0) 2 = v 2 hkvv ′′′ (0) + 3v ′ (0)v ′′ (0) = 0.v(0) = vv ′ (0) = 1 2v (h + k)v ′′ (0) = − 1 4v (h − k)2v ′′′ (0) = 3 8 v (h + k)(h − k)2 .25

SinceThe case n = 1 (3)ϕ ′ (α) = 2ψb ′ (v(α)) v′ (α)ϕ ′′ (α) = 2 [ ψb ′′(v(α))v′ (α) 2 + ψb ′ (v(α)) v′′ (α) ]ϕ ′′′ (α) = 2 [ ψ ′′′b (v(α)) v′ (α) 3 + 3ψ ′′b (v(α)) v′ (α)v ′′ (α) + ψ ′ b (v(α)) v′′′ (α) ] ,it follows thatϕ ′ (0) = 2ψb ′ (v) v′ (0)ϕ ′′ (0) = 2 [ ψb ′′(v)v′ (0) 2 + ψb ′ (v) v′′ (0) ]ϕ ′′′ (0) = 2 [ ψb ′′′(v)v′ (0) 3 + 3ψb ′′(v)v′ (0)v ′′ (0) + ψb ′ (v) v′′′ (0) ] .Substitution of of the above expressions <strong>for</strong> v(0), v ′ (0), v ′′ (0) and v ′′′ (0) yields(8)ϕ ′ (0) = ψb ′ (v) v (h + k)[ψ′′ϕ ′′ (0) = 1 2 b (v) v2 (h + k) 2 − ψb ′ (v) v (h − k)2]ϕ ′′′ (0) = 1 [4 ψ′′′b (v) v2 (h + k) 2 − 3 ξ b (v) v (h − k) 2] v (h + k) .Lemma 4 φ µ (x, s) is strictly convex.26

Computation of νTo compute the barrier parameter ν we need to find an upper bound <strong>for</strong>Substitutingwe haveν = maxy,z(ϕ ′ (0) ) [2ψ′ϕ ′′ (0) = b(v) v (h + k)[1 ψ′′b (v) v2 (h + k) 2 − ψb ′ (v) v (h − . (9)k)2]12[ψ′′2y = h + k, z = h − k,[ψ′b(v) vy ] 2] 2b (v) v2 y 2 − ψ ′ b (v) vz2] = 2 [ ψ ′ b (v) ] 2ψ ′′b (v) = 2N(v) 2 .Thus we have proved the following lemma.Lemma 5 If n = 1, and N(t) is as defined be<strong>for</strong>e, then ν(x, s) = 2N(v) 2 .Theorem 3 If n ≥ 1 then ν = 2 ‖N(v)‖ 2 .Proof: This is an immediate consequence of Lemma 3 and Lemma 5.•27

We definewhereResults on local self-concordancy (2)K(t) =¯ρ(t) √ 21 −ψb ′′′(t)(,3 − ¯ρ(t) ψ′′b (t))3 2√ρ(t) = ψ′ b(t) ψ′′′b (t)ξ b (t)ψb ′′(t), ¯ρ(t) = min[2, ρ(t)] , ξ b(t) = ψ b ′′ (t) − ψ′ b (t) .tTheorem 4 κ(x, s) = ‖K(v)‖ ∞ .i ψ i (t) ψ b (t) ψ ′ b1 t2 −12 1 2(t) ψ′′b2 − ln t −ln t −1 t( )t −1 2 ( 12tt −2 − 1 ) −1 3t 3 t 4(t) ψ′′′b(t) ξ(t) ρ(t) κ(t) κ(v)1t 2 − 2 2t 3 t 2 1 1 1−12t 5 4t 4 12t √32‖v‖ ∞√328

Proof of Theorem 4 (1)We first consider the case where n = 1. Then that κ = κ(x, s) is defined by2κ = maxh,kSubstitutingget⎧⎪⎨⎪⎩∣ ϕ ′′′ (0) ∣ ∣(ϕ ′′ (0)) 3 2=∣ 1 4[ψ′′′2 √ 2 κ = maxy,zb (v) v2 (h + k) 2 − 3 ξ(v) v (h − k) 2] v (h + k)[ [ 12 ψ′′b (v) v2 (h + k) 2 − ψb ′ (v) v (h − k)2]]3 2y = h + k, z = h − k,[ ∣ ψ′′′b (v) v2 y 2 − 3 ξ(v) vz 2] vy[ψ′′b (v) v2 y 2 − ψb ′ (v) vz2]3 2The last expression is homogeneous in (y, z). It follows that2 √ 2 κ = max {∣ [∣ ψ′′′b (v) v2 y 2 − 3 ξ(v) vz 2] vy∣ : ψ b ′′ (v) v2 y 2 − ψ b ′ (v) vz2 = 1 } .Be<strong>for</strong>e proceeding we recall the definitions of ρ(t) and ¯ρ(t):Note that ¯ρ(t) ∈ (0,2].∣ρ(t) = ψ′ b(t) ψ′′′b (t)ξ(t)ψ ′′ , ¯ρ(t) = min[2, ρ(t)] . (10)(t)b∣.29⎫∣⎪⎬⎪⎭.

Proof of Theorem 4 (2)2 √ 2 κ = max {∣ ∣ [ ψ ′′′b (v) v 2 y 2 − 3 ξ(v) vz 2] vy ∣ ∣ : ψ′′b (v) v 2 y 2 − ψ ′ b(v) vz 2 = 1 } . (11)The optimality conditions are, <strong>for</strong> some suitable multiplier λ,or, equivalently,3ψ ′′′b (v) v3 y 2 − 3 ξ(v) v 2 z 2 = 3λ ψ ′′b (v) v2 y−6 ξ(v) v 2 yz = 3λ [ −ψ ′ b (v) vz] ,ψ ′′′b (v) vy2 − ξ(v) z 2 = λ ψ ′′b (v) y2 ξ(v) vyz = λ ψ ′ b (v) z. (12)We see that either z = 0 or 2 ξ(v) vy = λ ψ ′ b (v).If z = 0 then the constraint in our problem implies that ψb ′′(v)v2 y 2 = 1, and hence (since(v) < 0), κ is in this case given byψ ′′′b2 √ 2 κ = − ψ′′′ b (v)(. (13)ψ′′b (v))3 230

Proof of Theorem 4 (3)Now assuming z ≠ 0, we can eliminate λ by substituting 2 ξ(v) vy = λ ψb ′ (v) into (12),which givesψ b ′ [ (v) ψ′′′b (v) vy2 − ξ(v) z 2] = λ ψ b ′ (v) ψ′′ b (v) y = 2 ξ(v)ψ′′ b (v) vy2 .Rearranging the terms, and using (10) we obtain−ψ ′ b (v)ξ(v) z2 = [ 2 ξ(v)ψ ′′b (v) − ψ′ b (v)ψ′′′ b (v) ]vy 2 = (2−ρ(v)) ξ(v)ψ ′′b (v) vy2 ,yielding−ψ ′ b (v) z2 = (2 − ρ(v)) ψ ′′b (v) vy2 , (14)Since −ψb ′ (v) > 0 and ψ′′b(v) > 0, this equation has no nonzero solution <strong>for</strong> y if ρ(v) > 2,and hence κ is then given by (13).If ρ(v) ≤ 2, substitution of (14) into the constraint ψ ′′b (v) v2 y 2 − ψ ′ b (v) vz2 = 1 yieldsor, equivalently,Henceψ ′′b (v) v2 y 2 + (2 − ρ(v)) ψ ′′b (v) v2 y 2 = 1,[3 − ρ(v)] ψ ′′b (v) v2 y 2 = 1. (15)vy =±1√[3 − ρ(v)] ψb ′′(16)(v).31

Proof of Theorem 4 (4)The rest of the proof consists of computing the value of the objective function using therelations found so far. Using (14), (10) and (15), respectively, we may write2 √ [2 κ = ± ψb ′′′ (2−ρ(v)) ψ′′(v) − 3 ξ(v)b (v) ]−ψb ′(v) v 3 y 3= ± 1 [ψb ′ ψ′ (v) b(v) ψb ′′′](v) + 3 (2 − ρ(v)) ξ(v)ψ′′b (v) v 3 y 3= ± ξ(v)ψ′′ b (v)ψb ′(v) [ρ(v) + 3(2 − ρ(v))] v 3 y 3= ±2 ξ(v) [ψb ′ (3 − ρ(v)) ψ′′(v) b (v) v2 y 2] vy = ±2 ξ(v)Finally, using (10) and (16) respectively, we get (since we are maximizing)2 √ 2 κ = ±2ξ(v)±2ξ(v)ψb ′ vy =(v)ψ ′ b(v)vy.ψb ′ √[3 (v) − ρ(v)] ψb ′′(v)= 2√ρ(v) (3 − ρ(v))−ψ ′′′b (v)(ψ′′b (v) )32.For ρ(v) = 2 this yields exactly the same value as in (13). Thus the following holds.Lemma 6 If n = 1, and with K(t) as defined above, we have κ(x, s) = K(v).Theorem 4 If n ≥ 1 then κ = ‖K(v)‖ ∞ .Proof: This is an immediate consequence of Lemma 3 and Lemma 6.•32

Summary of resultsFrom now on we assume that s = Mx + q. Our ingredients areTheorem 3 ν(x) = 2 ‖N(v)‖ 2 , where N(t) = √−ψ′ b (t) .ψb ′′(t)Theorem 4 κ(x) = ‖K(v)‖ ∞ , where K(t) =.1¯ρ(t) √ √ 2 3−¯ρ(t)−ψ ′′′b (t)(ψ′′b (t))3 2, withρ(t) = ψ′ b(t) ψ′′′b (t)ξ b (t)ψb ′′(t), ¯ρ(t) = min[2, ρ(t)] , ξ b(t) = ψ b ′′ (t) − ψ′ b (t) .tLemma 7 During the course of the algorithm we have λ(x) ≤ 1 4κ .This lemma impliesφ µ (x, s) = 2n∑i=1ψ (v i ) ≤ ω(−1 4 )κ 2 = 0.0376821κ 2 ≤ 126κ 2 33

Some examples of barier functions and their local κ and ν valuesi ψ b (t) ψb ′ (t) ψ′′b (t)ψ′′′ b (t) ξ b(t) ρ(t) ν(t) κ(t)1 −log t − 1 t1− 2 21 1 1t 2 t 3 t 22 1 2( t −2 − 1 ) − 1 t 3 3t 4 − 12t 5 4t 4 123t 22t √334t 1−q −1q−1−t −q qt −q−1 −q(q + 1)t −q−2 (q + 1)t −q−1 1e 1 t −ee− e1 t −1 1+2te 1 −1 t 2 t 4 t − 1+6t+6t2 e 1 −1 1+3tt 6 t e 1 −1 1+6t+6t2t 4 t1+5t+6t 25 − ∫ t −1 1 e1 ξdξ −e 1 −1 t e1 t −1− 1+2t e 1 −1 1+tt 2 t 4 t e 1 −1 1+2tt 2 t6e σ(1−t) −1−e σ(1−t) σe σ(1−t) −σ 2 eσ(1−t) 1+σteσ(1−t) σtσ t 1+σt2qt q−12 e 1 t −11+2t(1+3t)2t 2 e 1 −1 1+ttt √1+t2e σ(1−t)σ(q+1)t q−122 √ q√1+5t+6t 22+9t+12t 2√(2+4t) e 1 t −1(1+σt)√1+t2+t2e 1 t −1√t √ 2σe σ(1−t)1+σt3+2σt34

Analysis of the algorithm (1)Note that ψ(t) is monotonically decreasing <strong>for</strong> t ≤ 1 and monotonically increasing <strong>for</strong> t ≥ 1.In the sequel we denote by ̺ : [0, ∞) → [1, ∞) the inverse function of ψ(t) <strong>for</strong> t ≥ 1 andby χ : [0, ∞) → (0,1] the inverse function of ψ(t) <strong>for</strong> 0 < t ≤ 1. So we haveand̺(s) = t ⇔ s = ψ(t), s ≥ 0, t ≥ 1. (17)χ(s) = t ⇔ s = ψ(t), s ≥ 0, 0 < t ≤ 1. (18)Note that χ(s) is monotonically decreasing and ̺(s) is monotonically increasing in s ≥ 0.Lemma 8 Let t > 0 and ψ(t) ≤ s. Then χ(s) ≤ t ≤ ̺(s) .Proof: This is almost obvious. Since ψ(t) is strictly convex and minimal at t = 1, withψ(1) = 0, ψ(t) ≤ s implies that t belongs to a closed interval whose extremal points areχ(s) and ̺(s).•35

Graphical illustration of the functions χ(s) and ̺(s)ψ(t)111098s765432100 1 2 3 4 5χ(s)̺(s)t36

The local values of κ and ν are given byκ(x) = maxiWe need to find values of κ and ν such thatAnalysis of the algorithm (2)K(v i ), ν(x) = 2n∑i=1N (v i ) 2 .κ(x) ≤ κ,ν(x) ≤ ν<strong>for</strong> each v that occurs during the course of the algorithm. This certainly holds ifφ µ (x, s) = 2n∑i=1The left-hand side of this implication impliesψ (v i ) ≤ 126κ 2 ⇒ max K(v i ) ≤ κ, 2iψ (v i ) ≤ 152κ2, i = 1, . . . , n.According to Lemma 8 this implies( ) ( )1 1χ52κ 2 ≤ v i ≤ ̺52κ 2 , i = 1, . . . , n.n∑i=1N (v i ) 2 ≤ ν.37

χAnalysis of the algorithm (3)( 152κ 2 )≤ v i ≤ ̺( 152κ 2 ), i = 1, . . . , n.If we choose κ such that( ( )) 1K ̺52κ 2 ≤ κ (19)then the barrier function is locally κ-SC. The above inequality certainly has a solution, becauseif κ goes to infinity then the left-hand side approaches K(1), which is finite, whereas theright-hand side goes to ∞. Let ¯κ denote the smallest solution of (19).Finally, if we take ¯ν such that( ( ( ))) 1 2¯ν = 2n N χ52¯κ 2then the barrier function is a locally (¯κ,¯ν)-SC barrier function.38

Analysis of the algorithm (4)Substitution of the chosen values of κ and ν yields (also using that µ 0 = 1) the followingiteration bound <strong>for</strong> the algorithm:⌈2 ( 1 + 4¯κ √¯ν ) ln 2¯νǫ⌉=⎡⎢2(1 + 4¯κN( ( 1)) √)χ 2n52¯κ 2ln 2n( N ( χ ( 1ǫ))) 2⎤52¯κ 2 ⎥Note that apart from n the coefficients occurring in this expression depend only on the kernelfunction ψ, and not on n. Thus we may safely state that <strong>for</strong> every kernel function satisfyingour conditions the iteration bound is( √nlog)nO .ǫ.39

Concluding remarks• Recently we have used kernel function-<strong>based</strong> barrier functions (including so-called selfregularkernel functions) to improve the iteration bound <strong>for</strong> large-update <strong>methods</strong> fromO(nlog n ǫ ) to O(√ n(log n)log n ǫ). We were surprised to observe (most of the <strong>time</strong>after a tedious analysis, <strong>for</strong> each kernel function separately) that the iteration bounds<strong>for</strong> small-update <strong>methods</strong> <strong>based</strong> on these barrier functions always turned out to beO( √ nlog n ǫ ).• The current results seem to explain this phenomenon.• The results presented in this talk can be easily generalized to other (symmetric) coneoptimization problems, like second-order cone optimization and semidefinite optimization.• The next challenge is to find out if we can obtain the improved bounds <strong>for</strong> large-update<strong>methods</strong> by using this approach.40

Some references• Y.Q. Bai, M. El Ghami, and C. Roos. A comparative study of kernel functions <strong>for</strong> primaldualinterior-point algorithms in linear optimization. SIAM Journal on Optimization,15(1):101–128 (electronic), 2004.• J. Peng, C. Roos, and T. Terlaky. Self-Regularity. A New Paradigm <strong>for</strong> Primal-DualInterior-Point Algorithms. Princeton University Press, 2002.• M. Salahi, T. Terlaky, and G. Zhang. The complexity of self-regular proximity <strong>based</strong> infeasibleIPMs. Technical Report 2003/3, Advanced Optimization Laboratory, Mc MasterUniversity, Hamilton, Ontario, Canada, 2003.• S. Boyd and L. Vandenberghe. Convex optimization. Cambridge University Press, Cambridge,2004.• Y. Nesterov. Introductory Lectures on Convex Optimization. Kluwer Academic Publishers,Dordrecht, The Netherlands, 2004.• F. Glineur. Topics in convex optimization: interior-point <strong>methods</strong>, conic duality andapproximations. Faculté Polytechnique de Mons, Mons, Belgium, 2001. PhD thesis.• Y.E. Nesterov and A.S. Nemirovskii. Interior Point Polynomial Methods in Convex Programming.Theory and Algorithms. SIAM, Philadelphia, USA, 1993.41