FDWK_3ed_Ch05_pp262-319

Section 5.2 Definite Integrals 279
1
0
y
y = cos x
2
3
2
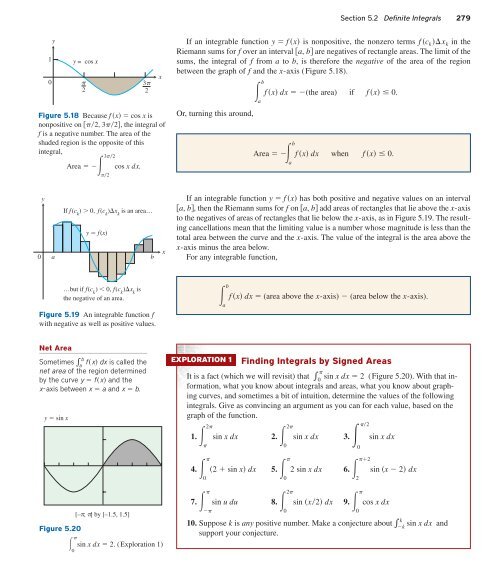
Figure 5.18 Because f x cos x is
nonpositive on 2, 32, the integral of
f is a negative number. The area of the
shaded region is the opposite of this
integral,
32
Area cos xdx.
2
x
If an integrable function y f x is nonpositive, the nonzero terms f c k x k in the
Riemann sums for f over an interval a, b are negatives of rectangle areas. The limit of the
sums, the integral of f from a to b, is therefore the negative of the area of the region
between the graph of f and the x-axis (Figure 5.18).
b
f x dx (the area) if f x 0.
a
Or, turning this around,
Area b
f x dx when f x 0.
a
0
y
a
If f(c k ) 0, f(c k )x k is an area…
y f(x)
b
x
If an integrable function y f x has both positive and negative values on an interval
a, b, then the Riemann sums for f on a, b add areas of rectangles that lie above the x-axis
to the negatives of areas of rectangles that lie below the x-axis, as in Figure 5.19. The resulting
cancellations mean that the limiting value is a number whose magnitude is less than the
total area between the curve and the x-axis. The value of the integral is the area above the
x-axis minus the area below.
For any integrable function,
…but if f(c k ) 0, f(c k )x k is
the negative of an area.
Figure 5.19 An integrable function f
with negative as well as positive values.
b
f x dx (area above the x-axis) (area below the x-axis).
a
Net Area
Sometimes b fx dx is called the
a
net area of the region determined
by the curve y fx and the
x-axis between x a and x b.
y sin x
[– , ] by [–1.5, 1.5]
Figure 5.20
sin xdx 2. (Exploration 1)
0
EXPLORATION 1
Finding Integrals by Signed Areas
It is a fact (which we will revisit) that sin xdx 2 (Figure 5.20). With that information,
what you know about integrals and areas, what you know about graph-
0
ing curves, and sometimes a bit of intuition, determine the values of the following
integrals. Give as convincing an argument as you can for each value, based on the
graph of the function.
1. 2
sin xdx 2. 2
2
sin xdx 3. sin xdx
0
0
4.
2 sin x dx 5.
2 sin xdx 6. 2
sin x 2 dx
0
7.
sin udu
0
8. 2
sin x2 dx
0
2
9.
cos xdx
10. Suppose k is any positive number. Make a conjecture about k sin xdx and
k
support your conjecture.
0