Chapter 4 - UCSB HEP

WORK AND ENERGY
'%nharmonicities"' introduced by this give further details on the shape
of the potential energy curve.
Since alf bound systems have a potential energy minimum at
equilibrium, we naturally expect that all bound systems behave
like harmonic oscillators for small displacements (unless the minimum
is so flat that the second derivative vanishes there also).
The harmonic oscillator approximation therefore has a wide range
of applicability, even down to internal motions in nuclei.
Once we have identified the kinetic and potential'energies of a
bound system, we can find the frequency of small osciClations by
inspection. For the elementary case of a mass on a spring we
have
and
2. =
In many problems, however, it is more natural to write the energies
in terms of a variable other than linear displacement. For
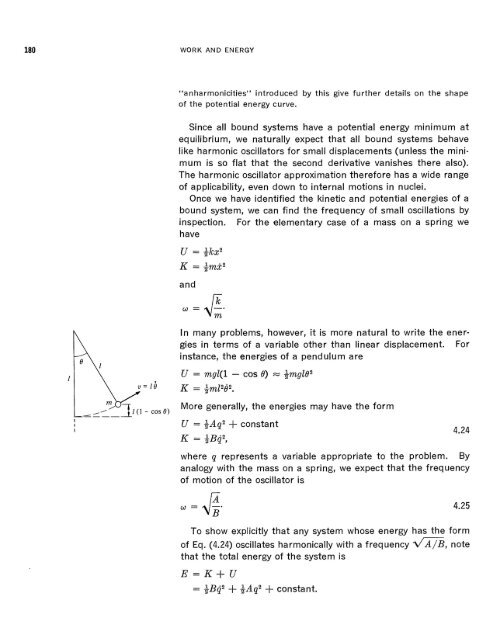
instance, the energies of a pendulum are
U = mgl(1 - cos 0) = +mgEB2
d---
1(1 - cos 6)
More generally, the energies may have the form
U = +Aq2 + constant
K = +l3q=,
where q represents a variable app~opriate to the problem. By
analogy with the mass on a spring, we expect that the frequency
of motion of the oscillator is
-
To show explicitly that any system whose energy has the form
of Eq. (4.24) oscillates harmonically with a frequency WB, note
that the total energy of the system is
E=K+U
= +Bq2 + +Aq2 + constant.