Parallelogram

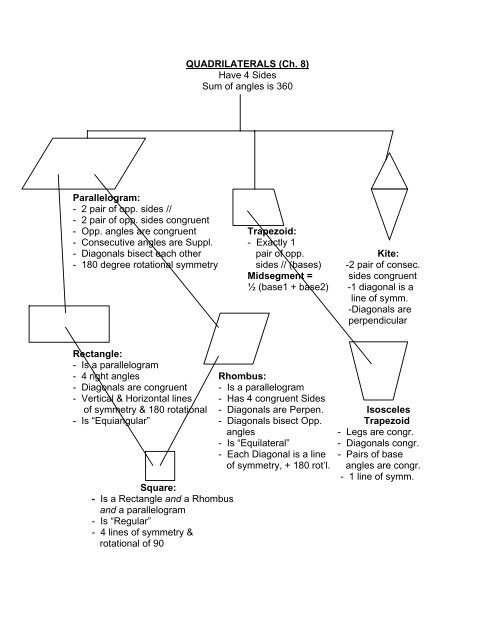
QUADRILATERALS (Ch. 8)
Have 4 Sides
Sum of angles is 360
Parallelogram:
- 2 pair of opp. sides //
- 2 pair of opp. sides congruent
- Opp. angles are congruent Trapezoid:
- Consecutive angles are Suppl. - Exactly 1
- Diagonals bisect each other pair of opp. Kite:
- 180 degree rotational symmetry sides // (bases) -2 pair of consec.
Midsegment =
½ (base1 + base2)
sides congruent
-1 diagonal is a
line of symm.
-Diagonals are
perpendicular
Rectangle:
- Is a parallelogram
- 4 right angles Rhombus:
- Diagonals are congruent - Is a parallelogram
- Vertical & Horizontal lines - Has 4 congruent Sides
of symmetry & 180 rotational - Diagonals are Perpen. Isosceles
- Is “Equiangular” - Diagonals bisect Opp. Trapezoid
angles
- Legs are congr.
- Is “Equilateral” - Diagonals congr.
Square:
- Is a Rectangle and a Rhombus
and a parallelogram
- Is “Regular”
- 4 lines of symmetry &
rotational of 90
- Each Diagonal is a line - Pairs of base
of symmetry, + 180 rot’l. angles are congr.
- 1 line of symm.

PROPERTIES of PARALLELOGRAMS
1. Definition of Parallelogram: A quadrilateral with both pairs of opposite
sides parallel.
B
A
C
We write the name of a
parallelogram with the symbol
followed by its four vertices in
clockwise or counter-clockwise
order. That way we can tell the four
sides, the opposite sides, the
diagonals, etc. just from the name.
EXAMPLE: ABCD or CBAD
D
2. Theorem: If a quadrilateral is a parallelogram, then its opposite sides are
congruent.
Given: ABCD Then: AB
≅ CD and BC ≅ AD
3. Theorem: If a quadrilateral is a parallelogram, then its opposite angles
are congruent.
Given: ABCD Then: A≅
C and B ≅ D
4. Theorem: If a quadrilateral is a parallelogram, then its consecutive
angles are supplementary.
Given: ABCD Then: A and B are supplementary,
B and C are supplementary,
C and D are supplementary,
D and A are supplementary,
5. Theorem: If a quadrilateral is a parallelogram, then its diagonals bisect
each other.
B
Given: ABCD
C
Then: AE
≅ EC and BE ≅ ED
E
A
D
Note: Most of these theorems (#2,3, 5) can be proven getting 2 triangles
congruent and then using CPCTC. (#4 follows from the Consecutive Interior
Angles Theorem from parallel lines.)

Proving a Quadrilateral is a Parallelogram
6. Definition: If both pairs of opposite sides of a quadrilateral are parallel,
then the quadrilateral is a parallelogram
B
E
C
Given: AB // CD and
BC//
AD
Then : Quad. ABCD is a
parallelogram
A
D
7. Theorem: If both pairs of opposite sides of a quadrilateral are congruent
then the quadrilateral is a parallelogram
Given: AB ≅ CD and BC ≅ AD
Then : Quad. ABCD is a parallelogram
8. Theorem: If both pairs of opposite angles of a quadrilateral are
congruent then the quadrilateral is a parallelogram
Given: BAD ≅ BCD and ABC ≅ CDA
Then : Quad. ABCD is a parallelogram
9. Theorem: If the diagonals of a quadrilateral bisect each other then the
quadrilateral is a parallelogram
Given: AE ≅ CE and BE ≅ ED
Then : Quad. ABCD is a parallelogram
10. Theorem: If one angle of a quadrilateral is supplementary to both of its
consecutive angles then the quadrilateral is a parallelogram.
Given: BAD and ABC are supplementary
and ABC and BCD are supplementary
Then : Quad. ABCD is a parallelogram
11. Theorem: If one pair of opposite sides of a quadrilateral are both
congruent and parallel, then the quadrilateral is a parallelogram.
Given: AB ≅ CD and AB // CD
Then : Quad. ABCD is a parallelogram

12. If and Only If: This phrase means that a statement is biconditional.
That is: p if and only if q or (symbolically) p ↔ q
Literally Means: p → q and q → p
(All definitions are “if and only if” statements (logically). A few theorems are.)
B
SPECIAL PARALLELOGRAMS
C
Definition: A rhombus is a
parallelogram with all four sides
congruent.
E
(Note: Some books just define
rhombus as an equilateral
quadrilateral.)
A
D
13. Theorem: A parallelogram is a rhombus if and only if its diagonals are
perpendicular.
Given: ABCD with AC ⊥ BD then ABCD is a rhombus
OR
Given: ABCD is a rhombus then AC ⊥ BD
14. Theorem: A parallelogram is a rhombus if and only if each diagonal
bisects a pair of opposite angles.
Given: ABCD and AC bisects BCD and BAD and
BD bisects ABC and ADC then ABCD is a rhombus
OR
Given: ABCD is a rhombus then AC bisects BCD and BAD
and BD bisects ABC and ADC

B
E
C
Definition: A rectangle is a
parallelogram with four right
angles.
A
D
(Note: Some books just define
rectangle as an equiangular
quadrilateral.)
15. Theorem: A parallelogram is a rectangle if and only if its diagonals are
congruent.
Given: ABCD with AC ≅ BD then ABCD is a rectangle.
OR
Given: ABCD is a rectangle then AC ≅ BD
16. Square: A regular quadrilateral. A square is both a rectangle and a
rhombus.
Other Special Quadrilaterals
D
C
Definition: A Trapezoid is a quadrilateral
with exactly one pair of opposite sides
parallel.
E
F
Bases: The two sides that are parallel
( DC and AB )
A
B
Legs: The two sides that are not parallel.
( AD and BC
Base Angles: The two angles that include
each base. A and B ; C and D
Midsegment of a trapezoid is the segment
which joins the midpoints of its legs.
(Segment EF )
16. Midsegment Theorem for Trapezoids: The Midsegment of a trapezoid
is parallel to each base and its length is one half of the sum of the lengths of
the bases.

D
C
Definition: An Isosceles Trapezoid
is a trapezoid with congruent legs.
A
B
16. Theorem: If a trapezoid is Isosceles, then each pair of base angles is
congruent.
D
C
Given: Quadrilateral
ABCD is an
isosceles trapezoid
A
B
Then: DAB ≅ CBA
and ADC ≅ CBA
17. Theorem: A trapezoid is Isosceles if and only if its diagonals are
congruent.
Given: Quadrilateral ABCD is an isosceles trapezoid
Then: AC ≅ DB
OR
Given: Quadrilateral ABCD is a trapezoid with AC ≅ DB
Then: Quadrilateral ABCD is isosceles
D
E
A
B
Definition: A kite is a quadrilateral with
2 distinct pairs of congruent consecutive
sides. (Note: Opposite sides are not
congruent.) AD≅ AB and DC ≅ BC
18. Theorem: The diagonals of a kite are
perpendicular.
C
19. Theorem: One diagonal of a kite is a
line of symmetry.