A theory of light propagation incorporating scattering and absorption ...

PROOF COPY [56361] 021507OPL
April 1, 2005 / Vol. 30, No. 7 / OPTICS LETTERS 1
Theory of light propagation incorporating
scattering and absorption in turbid media
Li Yang and Stanley J. Miklavcic
Department of Science and Technology, Linköping University, S-601 74 Norrköping, Sweden
PROOF COPY [56361] 021507OPL
Received August 16, 2004
A general theoretical approach to the description of light propagating through turbid media is proposed. The
theory is a modification of the two-flux model of Kubelka–Munk (KM), extending its applicability to media
systems containing an absorptive component. The modified KM model takes into account the influence of
internal scattering on the total path length and accommodates a wide range of absorption influences. Experimental
results obtained for dyed-paper systems illuminated by diffuse light are demonstrated to be
qualitatively and quantitatively reproduced by the theory. © 2005 Optical Society of America
OCIS codes: 290.4210, 290.7050, 300.1030.
The Kubelka–Munk theory (KMT) is the most popular
theory describing the behavior of light in turbid
media. It represents a two-flux approximation to the
radiative transfer theory describing light propagation.
When applied to homogeneous media, the
theory relates the rates of change of light fluxes in
two opposing directions at a position z to the local degrees
of absorption and forward and backward scattering.
These in turn are stipulated to be proportional
to the local flux intensities themselves, Iz
and Jz. The proportionality constants are now
termed the Kubelka–Munk coefficients of absorption
and scattering, K and S (m 2 /kg in paper-related applications).
Explicitly, the one-dimensional equations
of KMT are
− dI
dJ
=−S + KI + SJ, =−S + KJ + SI. 1
dz dz
In any practical implementation the coefficients are
ascribed physical attributes expressed in terms of
true physical properties. For example, when light distribution
is diffuse, Kubelka and Munk suggest that
K and S be linear functions of the intrinsic absorption
and scattering properties of the material. 1 Specifically,
K =2a, S = s. 2
Here, a and s represent the amount of light absorbed
and scattered, respectively, per unit path length and
are the respective reciprocals of the absorption and
scattering mean-free-path lengths l a =1/a and l s
=1/s.
One particular application of KMT appears in the
field of paper optics in which the aim is to obtain the
intrinsic optical properties of materials and then to
model the interaction of light with a paper medium.
In this field experimental predictions of the KMT
based on these linear relations have been shown to be
satisfactory when applied to a mixture of materials
with little absorption, such as white paper. However,
the theory breaks down when applied to mixtures
consisting of absorbing materials such as ink-dyed
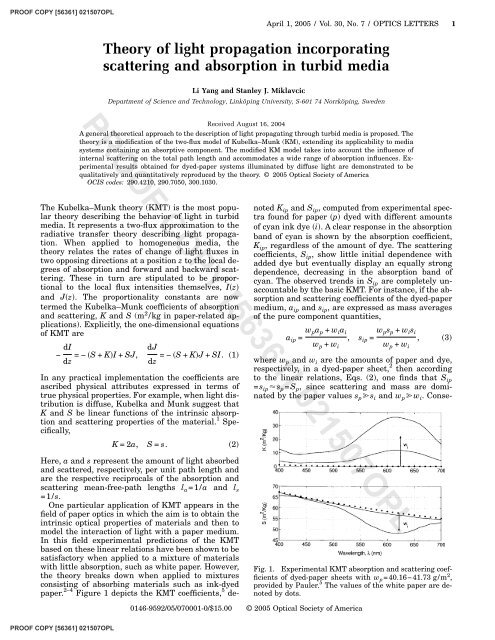
paper. 2–4 Figure 1 depicts the KMT coefficients, 5 denoted
K ip and S ip , computed from experimental spectra
found for paper p dyed with different amounts
of cyan ink dye i. A clear response in the absorption
band of cyan is shown by the absorption coefficient,
K ip , regardless of the amount of dye. The scattering
coefficients, S ip , show little initial dependence with
added dye but eventually display an equally strong
dependence, decreasing in the absorption band of
cyan. The observed trends in S ip are completely unaccountable
by the basic KMT. For instance, if the absorption
and scattering coefficients of the dyed-paper
medium, a ip and s ip , are expressed as mass averages
of the pure component quantities,
a ip = w pa p + w i a i
, s ip = w ps p + w i s i
, 3
w p + w i w p + w i
where w p and w i are the amounts of paper and dye,
respectively, in a dyed-paper sheet, 2 then according
to the linear relations, Eqs. (2), one finds that S ip
=s ip s p =S p , since scattering and mass are dominated
by the paper values s p s i and w p w i . Conse-
Fig. 1. Experimental KMT absorption and scattering coefficients
of dyed-paper sheets with w p =40.16−41.73 g/m 2 ,
provided by Pauler. 5 The values of the white paper are denoted
by dots.
0146-9592/05/070001-0/$15.00 © 2005 Optical Society of America
PROOF COPY [56361] 021507OPL

PROOF COPY [56361] 021507OPL
2 OPTICS LETTERS / Vol. 30, No. 7 / April 1, 2005
quently, at complete odds with observations, the
KMT predicts no variation in scattering with ink content
(see dotted lines in Fig. 1). Various strategies for
removing these and other shortcomings of KMT, by
expressing K and S as sophisticated functions of a
and s, have been mapped out. 6–8 However, the proposed
relations vary across fields of application, with
no apparent consensus on assumptions that should
be made.
Recently, we proposed a modification of the KMT to
explicitly include the effect of light scattering on the
true optical path length. 9 The fundamental revisions
of Eqs. (2) are mathematically expressed as 9
K = a, S = s/2. 4
The quantity is a factor depending solely on light
distribution I as =I/I 0 cos −1 d. For diffuse
light distribution, =2. The factor , called the
scattering-induced path variation (SIPV), is a new
development and appears in order to account for the
effect of scattering on the true path length. 9 depends
implicitly on the extents of both light absorption
and scattering in the medium and is simply defined
as the ratio of average total path length L to the
length of the corresponding displacement R (see
Fig. 2):
L/R.
5
For a strongly absorbing medium an expression in
terms of physical properties,
s/a 1/2 ,
6
was derived. In Yang and Kruse 9 it was also shown
that inclusion of the SIPV factor brings the KMT
qualitatively back in line with experimental observations.
However, the assumption of strong absorption
that leads to expression (6) greatly exaggerates the
quantitative absorptive influence of the ink dye. 9 To
alleviate this problem, we present here a new and
more widely applicable expression for the SIPV factor
that is both qualitatively and quantitatively in agreement
with the experiment.
For paper illuminated from above, the upward reflected
light is due to either bulk scatterers or boundary
interfaces. Because of scattering, photons propagate
in a zig-zag fashion in the medium, as suggested
by Fig. 2. If a photon is scattered N times, counted
from turning point B to exit point C, the start-to-end
displacement vector will be R= N
n=1 r n , and the total
photon path length is a sum of the lengths of the individual
displacements. In the mean, the total path
length will then be approximately N times the mean
free path between scatterers; that is,
L Nl s .
7
Within this same model of isotropic and chaotic scattering
the root-mean-square displacement is then
statistically
R R 2 1/2 = N n=1 r 2 n 1/2 Nls . 8
Here denote an average. On the other hand, the
mean displacement length averaged over all possible
directions in the upper hemisphere can also be computed
by 9 R R = 1 I D
d = D.
I 0 cos 9
Equating the last two results gives the number of
scattering events:
N = 2 D 2 /l s 2 .
10
The new and more general expression for the SIPV
factor is then
= sD.
11
Clearly important for determining and the amount
of reflected light is average depth D of the turning
points, defined in Fig. 2. Fortunately, this quantity
can be determined self-consistently with only the
KMT.
Let the incident light intensity be I 0 . The general
solutions of the KMT differential equations [Eqs. (1)],
subject to the boundary conditions (i.e., boundary reflection
at z=0 and z=−w p interfaces is negligible; extension
to cases with boundary reflection is straightforward
but tedious), are
Iz = b 1 expAz/R + R b 2 exp− Az, 12
Jz = b 1 expAz + b 2 exp− Az
PROOF COPY [56361] 021507OPL
where A=K 2 +2KS 1/2 and R =S+K−A/S and
b 1 =
I 0 R
1 − R 2 exp− 2Aw p , b 2 = − I 0R exp− 2Aw p
1 − R 2 exp− 2Aw p .
Fig. 2.
layer.
Schematic diagram of light scattering in a medium
Since Jz represents the number of (reflected) photons
per unit area per unit time traveling upward at
an arbitrary position z, average depth D of photons
that undergo reflection and exit from the upper surface
is given by
PROOF COPY [56361] 021507OPL

PROOF COPY [56361] 021507OPL
April 1, 2005 / Vol. 30, No. 7 / OPTICS LETTERS 3
0
D = −−w p
0
−w p
Jzzdz
Jzdz
= 1 − 2Aw p exp− Aw p − exp− 2Aw p
A1 − 2 exp− Aw p + exp− 2Aw p .
13
D depends on the geometric thickness of the layer,
w p , and the KMT coefficients of absorption and scattering,
K and S, through the parameter A=K 2
+2KS 1/2 . When the media layer is optically thick,
Aw p 1, Eq. (13) simplifies to D1/A, leading to the
equation
= s 2 /a 2 + as 1/4
14
for the SIPV factor. A number of limits are worth noting
here. For a relatively high-absorbing lowscattering
medium, as, the dependence derived
earlier, s/a 1/2 , is regained. Alternatively, a high
value is expected for a relatively low-absorbing
high-scattering medium, as; explicitly =s/a 1/4
1. Note that in all the cases some absorption is essential
for a consistent and meaningful evaluation of
the theory. For that matter, absorption is implicitly
inherent in the KMT also. Because no special assumptions
were made about the medium, the above
results apply to any type of mixed-media system.
Equation (11), with D given by Eq. (13), is a general
expression for the SIPV factor. When the layer
thickness and the KMT coefficients are known from
reflection and transmission measurements, found say
with diffuse light illumination, the SIPV factor can
be computed directly by =2SD 1/2 . Then, knowing
the KMT coefficients and the SIPV factor, one can
compute the intrinsic absorption and scattering coefficients,
a and s, with Eqs. (4).
We illustrate the effectiveness of the new approach
in reproducing experimental findings by applying the
revised KMT to the experimental system represented
in Fig. 1. This dyed-paper medium is typical of a system
that has thus far eluded the KMT. 2,3
In the simulation we adopt the nominal values of
w p =40 g/m 2 and =2 (diffuse light distribution). The
KMT coefficients of paper, K p and S p , and dye, K i and
S i , are first computed from experimental spectra for
pure paper and pure ink systems, 10 respectively, using
the standard KMT. a p , s p , a i , and s i are then determined
with Eqs. (4). The SIPV factor, ip , and the
KMT coefficients of the dyed-paper, K ip and S ip , are
then computed iteratively with Eqs. (3), (4), (11), and
(13). For details see our forthcoming paper.
The results of the simulations of systems of dyed
paper containing different amounts of dye are shown
in Fig. 3. Overall, the results compare favorably with
the experimental observations. Since paper undergoes
little absorption a p 0, dye induces little scattering
s i 0, and w p w i , one finds from Eqs. (3),
(4), and (11) that K ip 2 ip w i a i , S ip ip s p , and ip
2s p D ip . Hence K ip is proportional to the amount of
Fig. 3. Predictions of the KMT absorption and scattering
coefficients of dyed paper, with w p =40 g/m 2 and w i
=0.005,0.01,0.02,0.05,0.1,0.2 g/m 2 . The values of white
paper are denoted by dots.
dye, w i , and the dependence of S ip on the degree of
dyeing arises essentially through ip , which is proportional
to D ip . In turn, D ip , the average depth that
photons reach in the mixed medium before exiting
the illuminated surface, depends on the relative
strengths of absorption and scattering as well as the
layer thicknesses. As the amount of the (absorbing)
dye increases, the depth to which photons will survive
without being absorbed decreases. This causes a
reduction in ip and therefore a reduction in S ip
within the absorption band of the dye. The predicted
trend in S ip is completely in line with the experiments
shown in Fig. 1 and not featured by the standard
KMT. Note that when the amount of dye is
small, D ip is dominated by the thickness of the paper
layer, w p . ip and hence S ip then remain nearly independent
of dye, as in the experiments. In such cases,
Eqs. (4) predict similar results to those of standard
KMT [Eqs. (2)], which is known to apply well to systems
with little absorption.
L. Yang’s e-mail address is liyan@itn.liu.se.
References
1. P. Kubelka and F. Munk, Z. Tech. Phys. (Leipzig) 12,
593 (1931).
2. M. Rundlöf and J. A. Bristow, J. Pulp Pap. Sci. 23,
J220 (1997).
3. W. J. Foote, Pap. Trade J. 109, 333 (1939).
4. J. A. Van den Akker, in Modern Aspects of Reflectance
Spectroscopy, W. W. Wendlandt, ed. (Plenum, New
York, 1968).
5. N. Pauler (private communication). Similar
experimental results may be found in Ref. 2.
6. B. J. Brinkworth, Appl. Opt. 11, 1434 (1972).
7. B. Philips-Invernizzi, D. Dupont, and C. Caze, Opt.
Eng. (Bellingham) 40, 1082 (2001).
8. J. F. Bloch and R. S’eve, Color Res. Appl. 28, 227
(2003).
9. L. Yang and B. Kruse, J. Opt. Soc. Am. A 21, 1933
(2004).
10. L. Yang, J. Opt. Soc. Am. A 20, 1149 (2003).
PROOF COPY [56361] 021507OPL
PROOF COPY [56361] 021507OPL