Problems and Problem Solving - Ministry of Education

More documents

Recommendations

Info

should go about gathering the needed information – either through making assumptions and/or estimates, carrying out research or by performing calculations. Open problems usually produce different results, since each student may make different assumptions and estimates or may choose different facts and figures to include in the task. It is important, however, that students are able and allowed to justify their assumptions, estimates and choices in light of the answers that they received. Open problems are usually derived from two main sources by: i. transforming routine tasks into non-routine problems; and ii. using real-world situations. 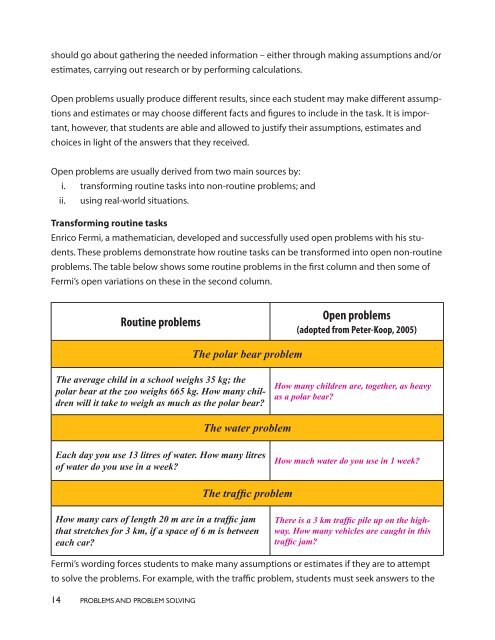Transforming routine tasks Enrico Fermi, a mathematician, developed and successfully used open problems with his students. These problems demonstrate how routine tasks can be transformed into open non-routine problems. The table below shows some routine problems in the first column and then some of Fermi’s open variations on these in the second column. Routine problems Open problems (adopted from Peter-Koop, 2005) The polar bear problem The average child in a school weighs 35 kg; the polar bear at the zoo weighs 665 kg. How many children will it take to weigh as much as the polar bear? How many children are, together, as heavy as a polar bear? The water problem Each day you use 13 litres of water. How many litres of water do you use in a week? How much water do you use in 1 week? The traffic problem How many cars of length 20 m are in a traffic jam that stretches for 3 km, if a space of 6 m is between each car? There is a 3 km traffic pile up on the highway. How many vehicles are caught in this traffic jam? Fermi’s wording forces students to make many assumptions or estimates if they are to attempt to solve the problems. For example, with the traffic problem, students must seek answers to the 14 PROBLEMS AND PROBLEM SOLVING ProblemSolving.indd 14 8/24/12 6:55:34 PM
following questions. •y •y •y •y Are all vehicles of the same length? What is the average length of a vehicle? Typically, in a line of traffic, will most vehicles be ‘large’, ‘small’ or ‘medium size’? Approximately how much space would there be between vehicles? If you look closely at each of Fermi’s problems, it is clear that they resemble (but are significantly different from) routine problems. Indeed, it is not hard to imagine that these are simply routine problems that have been modified in one way or another. Real-world situations By reading through Fermi’s problems, you will also realize that each problem asks students to reflect on and mathematize their real world experiences. So, by placing students in what ought to be familiar or accessible context, you will encourage them to start thinking about and operating with numbers; they will also start to consider whether answers are ‘reasonable’ by reflecting on their experiences and observations or by carrying out experiments. Puzzles A mathematical puzzle is an activity in which, typically, numbers and/or objects are used to complete a task by organizing or using them in a particular way. Puzzles are created by considering cognitive roots – core and important ideas that can be extended to generate problems – and by placing the problem solver in complicated situations where complex relationships must be understood and modeled. Most mathematical puzzles involve one or more of the following. i. Manipulation of objects to create patterns or designs. In the Rubik Cube puzzle, for example, persons try to rearrange multicoloured blocks that are used to make a cube so that each face of the cube has a separate solid colour. The cube is made up of 54 blocks with a total of six different colours – each face can be 'twisted' so that colours can be aligned. Another example of a puzzle which involves manipulation is the Testa Puzzle on the following page. ii. Arrangement of numbers according to set rules. Sudoku, for example, requires that players insert 9 ones, 9 twos, 9 threes, … 9 nines in a large 9 × 9 grid (made up of three 3 × 3 squares) so that no row or column has the same number. Additionally, each 3 × 3 square must have each of the numbers 1 – 9. Another example of a number-based puzzle, The Magic Triangle , is shown on the following page. Ministry of Education 2011 15 ProblemSolving.indd 15 8/24/12 6:55:35 PM
Page 1 and 2: Ministry of Education Problems and
Page 3 and 4: Co n t e n t s Introduction........
Page 5 and 6: In t r o d u c t i o n Overview Acc
Page 7 and 8: seen it that way; explore why this
Page 9 and 10: Bearing in mind the definitions abo
Page 11 and 12: features of non-routine Problems No
Page 13: situation in which a census taker s
Page 17 and 18: iii. Use of geometric principles an
Page 19 and 20: Ministry of Education 2011 19 Probl
Page 21 and 22: Model solutions Essentially, the ap
Page 23 and 24: The table above shows that the numb
Page 25 and 26: Number of coins New values after ea
Page 27 and 28: se c t I o n 2 pr o B l e m cr e A
Page 29 and 30: o Explore a variety of situations.
Page 31 and 32: As we can see from the example, the
Page 33 and 34: or less they may still apply the LC
Page 35 and 36: This extension requires students to
Page 37 and 38: • y Familiarize yourself and pay
Page 39 and 40: Child 1 (age in years) Child 2 (age
Page 41 and 42: Logical reasoning will determine th
Page 43 and 44: • Solving a simpler problem, howe
Page 45 and 46: The table below shows how many visi
Page 47 and 48: To determine the number of visits f
Page 49 and 50: Work Backwards The process of rever
Page 51 and 52: se c t I o n 4 pr o B l e m so l V
Page 53 and 54: Van de Walle, et al. (2010) suggest
Page 55 and 56: Gender: The culture that obtains in
Page 57 and 58: se c t I o n 5 pr o B l e m BA n k
Page 59 and 60: Problem 2 - Cutting Squares Grades:
Page 61 and 62: Problem 3 - Taking Counters Grade:
Page 63 and 64: Problem 5 - A Tricky river Crossing
Page 65 and 66:
It can be unfolded to give on one s
Page 67 and 68:
Problem 8 - Bicycles and Tricycles
Page 69 and 70:
Problem 10 - Filling the Pool Grade
Page 71 and 72:
Problem 12 - The Knight’s Dance G
Page 73 and 74:
Problem 13 - Trading Places Grade:
Page 75 and 76:
Problem 16 - Folded Corners Grade:
Page 77 and 78:
Problem 18 - Counting Rectangles Gr
Page 79 and 80:
Problem 19 - Box it Up Grade: 3 or
Page 81 and 82:
Problem 21 - T-Patterns Grades: 5 -
Page 83 and 84:
Problem 23 - Last One Standing Grad
Page 85 and 86:
Ministry of Education 2011 85 Probl
Page 87 and 88:
Problem 26 - Noughts and Crosses Gr
Page 89 and 90:
Problem 27 - A Weighing Problem Gra
Page 91 and 92:
Problem 29 - Frog Hopping Grade: 4
Page 93 and 94:
2. In general, how many squares are
Page 95 and 96:
Problem 33 - Chicken Combos Grades:
Page 97 and 98:
2. Explain how you know the fractio
Page 99 and 100:
Problem 36 - Measuring Jugs Grades:
Page 101 and 102:
Problem 38 - The Trapezium Problem
Page 103 and 104:
Problem 39 - Karen’s Troubles Gra
Page 105 and 106:
Problem 41 - Stand Out Grade: 3 or
Page 107 and 108:
Problem 43 - Mathematics Maze Grade
Page 109 and 110:
Problem 45 - Circling Numbers Grade
Page 111 and 112:
Problem 47 - Triangle Problems Grad
Page 113 and 114:
Problem 48 - Factors Grade: 3 or ab
Page 115 and 116:
Problem 50 - Target Grade: 4 or abo
Page 117 and 118:
Problem 52 - Pond Borders Grade: 5
Page 119 and 120:
Problem 54 - Teacher’s Banner Gra
Page 121 and 122:
Grades: 4 - 6 Strand: Number Studen
Page 123 and 124:
Problem 58 - Patty Please Grade: 4
Page 125 and 126:
Problem 60 - Text-a-holic Grade: 3
Page 127 and 128:
Problem Number 62 - Magic Squares G
Page 129 and 130:
Ap p e n d i x 1 - Se l e c t e d S
Page 131 and 132:
Problem 4 - Perfect squares 1. When
Page 133 and 134:
Problem 11- The 400 Problem 1. Sinc
Page 135 and 136:
When we look at the results recorde
Page 137 and 138:
Problem 18 - Counting Rectangles 1.
Page 139 and 140:
2. We can note that: a) The pattern
Page 141 and 142:
As we go around the circle we may s
Page 143 and 144:
For example, if a 1g weight is plac
Page 145 and 146:
Problem 30 - Chess Board Squares 1.
Page 147 and 148:
Problem 32 - Newspaper Math 1. 2. 3
Page 149 and 150:
Problem 38 - The Trapezium Problem
Page 151 and 152:
Problem 56 - Cross Out 8 The winnin
Page 153 and 154:
Heuristics Strategies employed in p
Page 155 and 156:
Scaffolding A teaching strategy in
show all

Problems and Problem Solving - Ministry of Education

Create successful ePaper yourself

Delete template?

Save as template?