9 FURTHER APPLICATIONS OF INTEGRATION

CHAPTER 9
FURTHER APPLICATIONS OF INTEGRATION
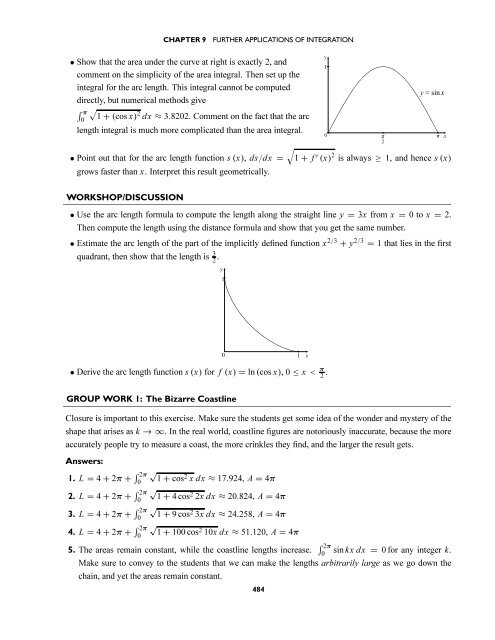
• Show that the area under the curve at right is exactly 2, and
comment on the simplicity of the area integral. Then set up the
integral for the arc length. This integral cannot be computed
directly, but numerical methods give
∫ π
√
0 1 + (cos x) 2 dx ≈ 3.8202. Comment on the fact that the arc
length integral is much more complicated than the area integral.
• Point out that for the arc length function s (x), ds/dx =
grows faster than x. Interpret this result geometrically.
√
1 + f ′ (x) 2 is always ≥ 1, and hence s (x)
WORKSHOP/DISCUSSION
• Use the arc length formula to compute the length along the straight line y = 3x from x = 0tox = 2.
Then compute the length using the distance formula and show that you get the same number.
• Estimate the arc length of the part of the implicitly defined function x 2/3 + y 2/3 = 1thatliesinthefirst
quadrant, then show that the length is 3 2 . y
1
0
• Derive the arc length function s (x) for f (x) = ln (cos x),0≤ x < π 2 .
1 x
GROUP WORK 1: The Bizarre Coastline
Closure is important to this exercise. Make sure the students get some idea of the wonder and mystery of the
shape that arises as k →∞. In the real world, coastline figures are notoriously inaccurate, because the more
accurately people try to measure a coast, the more crinkles they find, and the larger the result gets.
Answers:
1. L = 4 + 2π + ∫ 2π
√
0 1 + cos 2 xdx≈ 17.924, A = 4π
2. L = 4 + 2π + ∫ 2π
√
0 1 + 4cos 2 2xdx≈ 20.824, A = 4π
3. L = 4 + 2π + ∫ 2π
√
0 1 + 9cos 2 3xdx≈ 24.258, A = 4π
4. L = 4 + 2π + ∫ 2π
√
0 1 + 100 cos 2 10xdx≈ 51.120, A = 4π
∫ 2π
5. The areas remain constant, while the coastline lengths increase.
0
sin kx dx = 0 for any integer k.
Make sure to convey to the students that we can make the lengths arbitrarily large as we go down the
chain, and yet the areas remain constant.
484