- Page 1:
Foundations of GeometryLecture Note
- Page 4 and 5:
ivCONTENTS30 Triangles in Neutral G
- Page 6 and 7:
2 SECTION 1. PREFACEare enrolled in
- Page 8 and 9:
4 SECTION 1. PREFACEre-learning it
- Page 10 and 11:
6 SECTION 2. NCTM3. To guide in the
- Page 12 and 13:
8 SECTION 2. NCTMTechnology. Techno
- Page 14 and 15:
10 SECTION 2. NCTM« CC BY-NC-ND 3.
- Page 16 and 17:
12 SECTION 3. CA STANDARDIn 2005 Ca
- Page 18 and 19:
14 SECTION 3. CA STANDARDThe Califo
- Page 20 and 21:
16 SECTION 3. CA STANDARDCalifornia
- Page 22 and 23:
18 SECTION 4. COMMON COREAt all lev
- Page 24 and 25:
20 SECTION 5. LOGIC AND PROOFour th
- Page 26 and 27:
22 SECTION 5. LOGIC AND PROOFRene D
- Page 28 and 29:
24 SECTION 5. LOGIC AND PROOF“I
- Page 30 and 31:
26 SECTION 6. REAL NUMBERSThe inter
- Page 32 and 33:
28 SECTION 6. REAL NUMBERS“The Su
- Page 34 and 35:
30 SECTION 7. EUCLID’S ELEMENTSEu
- Page 36 and 37:
32 SECTION 7. EUCLID’S ELEMENTSFi
- Page 38 and 39:
34 SECTION 8. HILBERT’S AXIOMSiom
- Page 40 and 41:
36 SECTION 8. HILBERT’S AXIOMS«
- Page 42 and 43:
38 SECTION 9. BIRKHOFF/MACLANE AXIO
- Page 44 and 45:
40 SECTION 9. BIRKHOFF/MACLANE AXIO
- Page 46 and 47:
42 SECTION 10. THE SMSG AXIOMSP is
- Page 48 and 49:
44 SECTION 10. THE SMSG AXIOMS« CC
- Page 50 and 51:
46 SECTION 11. THE UCSMP AXIOMSin s
- Page 52 and 53:
48 SECTION 11. THE UCSMP AXIOMS« C
- Page 54 and 55:
50 SECTION 12. VENEMA’S AXIOMS3.
- Page 56 and 57:
52 SECTION 12. VENEMA’S AXIOMS«
- Page 58 and 59:
54 SECTION 13. INCIDENCE GEOMETRYFi
- Page 60 and 61:
56 SECTION 13. INCIDENCE GEOMETRYEx
- Page 62 and 63:
58 SECTION 13. INCIDENCE GEOMETRYFi
- Page 64 and 65:
60 SECTION 13. INCIDENCE GEOMETRY«
- Page 66 and 67:
62 SECTION 14. BETWEENNESSFigure 14
- Page 68 and 69:
64 SECTION 14. BETWEENNESSTheorem 1
- Page 70 and 71:
66 SECTION 14. BETWEENNESS(a) To sh
- Page 72 and 73:
68 SECTION 14. BETWEENNESSThe follo
- Page 74 and 75:
70 SECTION 14. BETWEENNESSExample 1
- Page 76 and 77:
72 SECTION 14. BETWEENNESSorf(A) >
- Page 78 and 79:
74 SECTION 14. BETWEENNESS« CC BY-
- Page 80 and 81:
76 SECTION 15. THE PLANE SEPARATION
- Page 82 and 83:
78 SECTION 15. THE PLANE SEPARATION
- Page 84 and 85:
80 SECTION 16. ANGLESFigure 16.1: T
- Page 86 and 87:
82 SECTION 16. ANGLESCorollary 16.6
- Page 88 and 89:
84 SECTION 16. ANGLESFigure 16.6: I
- Page 90 and 91:
86 SECTION 16. ANGLESD cannot be in
- Page 92 and 93:
88 SECTION 17. THE CROSSBAR THEOREM
- Page 94 and 95:
90 SECTION 17. THE CROSSBAR THEOREM
- Page 96 and 97:
92 SECTION 18. LINEAR PAIRSFigure 1
- Page 98 and 99:
94 SECTION 18. LINEAR PAIRSγ + ∠
- Page 100 and 101:
96 SECTION 19. ANGLE BISECTORSwith
- Page 102 and 103:
98 SECTION 19. ANGLE BISECTORSAngle
- Page 104 and 105:
100 SECTION 20. THE CONTINUITY AXIO
- Page 106 and 107:
102 SECTION 20. THE CONTINUITY AXIO
- Page 108 and 109:
104 SECTION 21. SIDE-ANGLE-SIDEBirk
- Page 110 and 111:
106 SECTION 21. SIDE-ANGLE-SIDEFigu
- Page 112 and 113:
108 SECTION 22. NEUTRAL GEOMETRYEll
- Page 114 and 115:
110 SECTION 22. NEUTRAL GEOMETRY«
- Page 116 and 117:
112 SECTION 23. ANGLE-SIDE-ANGLEFig
- Page 118 and 119:
114 SECTION 23. ANGLE-SIDE-ANGLE«
- Page 120 and 121:
116 SECTION 24. EXTERIOR ANGLESTheo
- Page 122 and 123:
118 SECTION 24. EXTERIOR ANGLES« C
- Page 124 and 125:
120 SECTION 25. ANGLE-ANGLE-SIDEBy
- Page 126 and 127:
122 SECTION 26. SIDE-SIDE-SIDECase
- Page 128 and 129:
124 SECTION 26. SIDE-SIDE-SIDEBy si
- Page 130 and 131:
126 SECTION 27. SCALENE AND TRIANGL
- Page 132 and 133:
128 SECTION 27. SCALENE AND TRIANGL
- Page 134 and 135:
130 SECTION 28. CHARACTERIZATION OF
- Page 136 and 137:
132 SECTION 28. CHARACTERIZATION OF
- Page 138 and 139:
134 SECTION 29. TRANSVERSALSFigure
- Page 140 and 141:
136 SECTION 29. TRANSVERSALSCorolla
- Page 142 and 143:
138 SECTION 30. TRIANGLES IN NEUTRA
- Page 144 and 145:
140 SECTION 30. TRIANGLES IN NEUTRA
- Page 146 and 147:
142 SECTION 30. TRIANGLES IN NEUTRA
- Page 148 and 149:
144 SECTION 30. TRIANGLES IN NEUTRA
- Page 150 and 151:
146 SECTION 31. QUADRILATERALS IN N
- Page 152 and 153:
148 SECTION 31. QUADRILATERALS IN N
- Page 154 and 155:
150 SECTION 31. QUADRILATERALS IN N
- Page 156 and 157:
152 SECTION 31. QUADRILATERALS IN N
- Page 158 and 159:
154 SECTION 31. QUADRILATERALS IN N
- Page 160 and 161:
156 SECTION 32. THE EUCLIDEAN PARAL
- Page 162 and 163:
158 SECTION 32. THE EUCLIDEAN PARAL
- Page 164 and 165:
160 SECTION 32. THE EUCLIDEAN PARAL
- Page 166 and 167:
162 SECTION 32. THE EUCLIDEAN PARAL
- Page 168 and 169:
164 SECTION 32. THE EUCLIDEAN PARAL
- Page 170 and 171:
166 SECTION 32. THE EUCLIDEAN PARAL
- Page 172 and 173:
168 SECTION 33. RECTANGLESLemma 33.
- Page 174 and 175:
170 SECTION 33. RECTANGLESFigure 33
- Page 176 and 177:
172 SECTION 33. RECTANGLES« CC BY-
- Page 178 and 179:
174 SECTION 34. THE PARALLEL PROJEC
- Page 180 and 181:
176 SECTION 34. THE PARALLEL PROJEC
- Page 182 and 183:
178 SECTION 35. SIMILAR TRIANGLESBy
- Page 184 and 185:
180 SECTION 35. SIMILAR TRIANGLESCo
- Page 186 and 187:
182 SECTION 36. TRIANGLE CENTERSFig
- Page 188 and 189:
184 SECTION 36. TRIANGLE CENTERSThe
- Page 190 and 191:
186 SECTION 36. TRIANGLE CENTERSCen
- Page 192 and 193:
188 SECTION 37. AREADefinition 37.5
- Page 194 and 195:
190 SECTION 37. AREAToday’s Lesso
- Page 196 and 197:
192 SECTION 38. THE PYTHAGOREAN THE
- Page 198 and 199:
194 SECTION 38. THE PYTHAGOREAN THE
- Page 200 and 201:
196 SECTION 38. THE PYTHAGOREAN THE
- Page 202 and 203:
198 SECTION 38. THE PYTHAGOREAN THE
- Page 204 and 205:
200 SECTION 38. THE PYTHAGOREAN THE
- Page 206 and 207:
202 SECTION 39. CIRCLESFigure 39.1:
- Page 208 and 209:
204 SECTION 39. CIRCLESFigure 39.3:
- Page 210 and 211:
206 SECTION 39. CIRCLESFigure 39.5:
- Page 212 and 213:
208 SECTION 39. CIRCLESTheorem 39.1
- Page 214 and 215:
210 SECTION 39. CIRCLESLet D be the
- Page 216 and 217:
212 SECTION 39. CIRCLES« CC BY-NC-
- Page 218 and 219:
214 SECTION 40. CIRCLES AND TRIANGL
- Page 220 and 221:
216 SECTION 40. CIRCLES AND TRIANGL
- Page 222 and 223:
218 SECTION 40. CIRCLES AND TRIANGL
- Page 224 and 225:
220 SECTION 41. EUCLIDEAN CIRCLESFi
- Page 226 and 227:
222 SECTION 41. EUCLIDEAN CIRCLESFi
- Page 228 and 229:
224 SECTION 41. EUCLIDEAN CIRCLESFi
- Page 230 and 231: 226 SECTION 41. EUCLIDEAN CIRCLESFi
- Page 232 and 233: 228 SECTION 41. EUCLIDEAN CIRCLESBy
- Page 234 and 235: 230 SECTION 42. AREA AND CIRCUMFERE
- Page 236 and 237: 232 SECTION 42. AREA AND CIRCUMFERE
- Page 238 and 239: 234 SECTION 42. AREA AND CIRCUMFERE
- Page 240 and 241: 236 SECTION 42. AREA AND CIRCUMFERE
- Page 242 and 243: 238 SECTION 43. INDIANA BILL 246the
- Page 244 and 245: 240 SECTION 44. ESTIMATING πFigure
- Page 246 and 247: 242 SECTION 44. ESTIMATING πso tha
- Page 248 and 249: 244 SECTION 44. ESTIMATING πn π n
- Page 250 and 251: 246 SECTION 44. ESTIMATING πTable
- Page 252 and 253: 248 SECTION 44. ESTIMATING πnums =
- Page 254 and 255: 250 SECTION 44. ESTIMATING π« CC
- Page 256 and 257: 252 SECTION 45. EUCLIDEAN CONSTRUCT
- Page 258 and 259: 254 SECTION 45. EUCLIDEAN CONSTRUCT
- Page 260 and 261: 256 SECTION 45. EUCLIDEAN CONSTRUCT
- Page 262 and 263: 258 SECTION 45. EUCLIDEAN CONSTRUCT
- Page 264 and 265: 260 SECTION 45. EUCLIDEAN CONSTRUCT
- Page 266 and 267: 262 SECTION 45. EUCLIDEAN CONSTRUCT
- Page 268 and 269: 264 SECTION 46. HYPERBOLIC GEOMETRY
- Page 270 and 271: 266 SECTION 46. HYPERBOLIC GEOMETRY
- Page 272 and 273: 268 SECTION 46. HYPERBOLIC GEOMETRY
- Page 274 and 275: 270 SECTION 46. HYPERBOLIC GEOMETRY
- Page 276 and 277: 272SECTION 47.PERPENDICULAR LINES I
- Page 278 and 279: 274SECTION 47.PERPENDICULAR LINES I
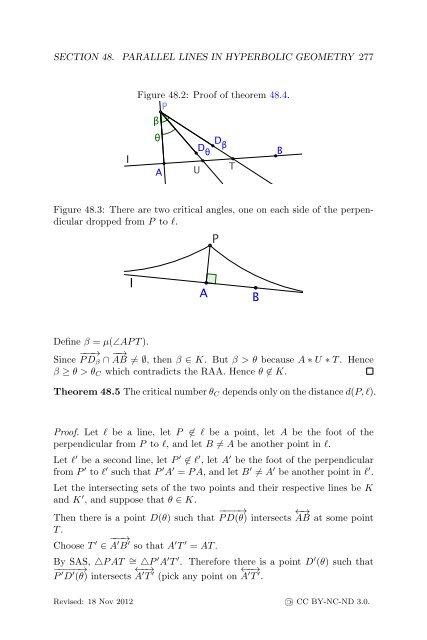
- Page 282 and 283: 278 SECTION 48. PARALLEL LINES IN H
- Page 284 and 285: 280 SECTION 48. PARALLEL LINES IN H
- Page 286 and 287: 282 SECTION 48. PARALLEL LINES IN H
- Page 288 and 289: 284 SECTION 49. TRIANGLES IN HYPERB
- Page 290 and 291: 286 SECTION 49. TRIANGLES IN HYPERB
- Page 292 and 293: 288 SECTION 49. TRIANGLES IN HYPERB
- Page 294 and 295: 290 SECTION 50. AREA IN HYPERBOLIC
- Page 296 and 297: 292 SECTION 50. AREA IN HYPERBOLIC
- Page 298 and 299: 294 SECTION 50. AREA IN HYPERBOLIC
- Page 300 and 301: 296 SECTION 50. AREA IN HYPERBOLIC
- Page 302 and 303: 298 SECTION 51. THE POINCARE DISK M
- Page 304 and 305: 300 SECTION 51. THE POINCARE DISK M
- Page 306 and 307: 302 SECTION 51. THE POINCARE DISK M
- Page 308 and 309: 304 SECTION 51. THE POINCARE DISK M
- Page 310 and 311: 306 SECTION 52. ARC LENGTHAs we see
- Page 312 and 313: 308 SECTION 52. ARC LENGTHProof. Su
- Page 314 and 315: 310 SECTION 52. ARC LENGTHThus the
- Page 316 and 317: 312 SECTION 52. ARC LENGTHMeasuring
- Page 318 and 319: 314 SECTION 53. SPHERICAL GEOMETRYW
- Page 320 and 321: 316 SECTION 53. SPHERICAL GEOMETRYF
- Page 322 and 323: 318 SECTION 53. SPHERICAL GEOMETRYP
- Page 324 and 325: 320 APPENDIX A. SYMBOLS USEDAppendi
- Page 326 and 327: 322 APPENDIX A. SYMBOLS USEDTechnol