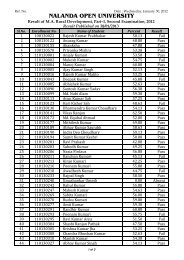
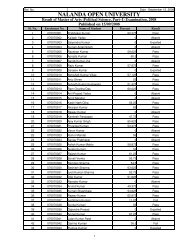
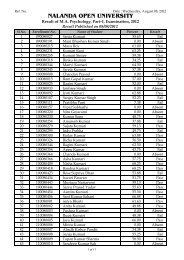
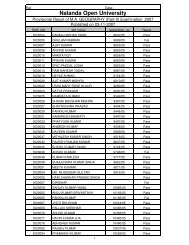
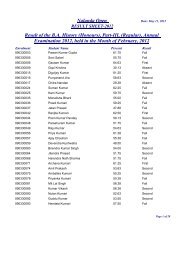
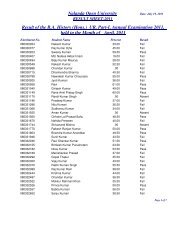
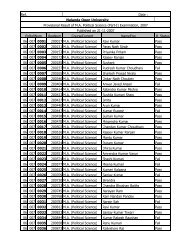
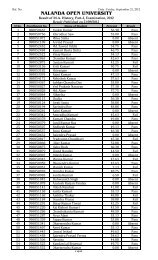
Assignment Questions, 20101 - Nalanda Open University

2- 'kks/k ;kstuk D;k gS \ fdlh 'kks/k&izLrko dh lajpuk dk o.kZu djsa AWhat is a research plan ? Describe the structure of a research proposal.3- 'kks/k ds fofHkUu izdkjksa rFkk mikxeksa dh foLrkj ls O;k[;k djsa AExplain in detail the different types and approaches to research.M.Sc(Math) Part-IPAPER-IAnswer Any Two Questions.(lHkh iz'u 10-10 vadska ds gS)1. (a) Define a composition series and prove that every finite group G has a compositionseries.(b) State and prove Schreier refinement theorem .2. State and prove Jordan-Holder theorem for finite group.3. In a commutative ring R with unity, show that an ideal is maximal ifand only if is a field.PAPER-IIAnswer Any Two Questions.(lHkh iz'u 10-10 vadska ds gS)1. (a) State and prove Bolzano-Weierstrass theorem.(b) Deduce Bolzano-Weierstrass theorem from Heine-Borel theorem.2. Show that a function f on [a, b] is of bounded variation if and only if it can berepresented as a difference of two monotonically increasing functions on [a, b].3. (a) State and prove the first mean value theorem for Riemann-Stieltges integral.(b)State and prove a necessary and sufficient condition for f R (α ) on [a, b].PAPER-IIIAnswer Any Two Questions.(lHkh iz'u 10-10 vadska ds gS)1. (a) If E1 and E2 are measurable, then show that E1 E2 is measurable.(b) Show that an enumerable set is measurable with measure equal to 0.2. (a) Prove that a continuous function is measurable but every measurable function is notcontinuous.(b) If f is measurable, then show that is measurable.3. (a) Show that every function of bounded variation on [a, b] is bounded on [a, b]. Is theconverse true? Justify your answer.variation over an interval [a, b].(b) Show that a function may be continuous without being of bounded variation over aninterval [a, b].PAPER-IVAnswer Any Two Questions.(lHkh iz'u 10-10 vadska ds gS)1. (a) Show that the open interval (0, 1) on the real line R is not compact.(b) Prove that every compact subspace of a Hausdorff space is closed.2. (a) Show that the product of any non-empty class of Hausdorff spaces is a Hausdorff(b)space.Give an example to show that a one-to-one continuous mapping of one topologicalspace onto another need not be a homeomorphism.3. (a) Give an example of a normal space which is not regular or T1.(b) Show that every metric space is a normal space.