3 Applications of Definite Integrals to rates, velocities, and densities

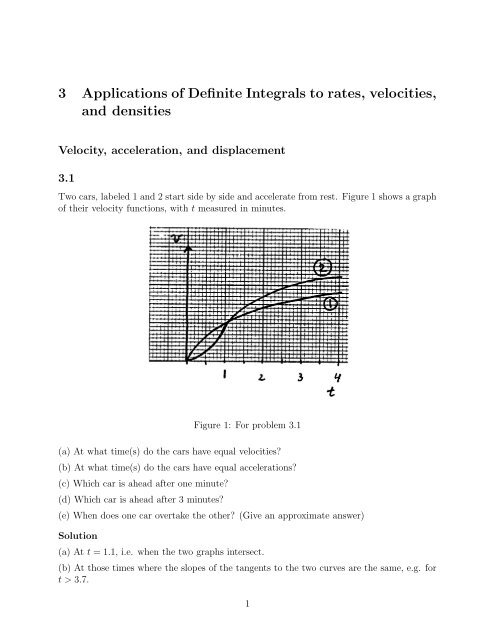
(c) Car 1, because the area under the graph if its velocity between 0 and 1 is bigger thanthe corresponding area for car 2.(d) Car 2, because the area under the graph if its velocity between 0 and 3 is bigger thanthe corresponding area for car 1.(e) Car 2 overtakes car 1 at the point t at which the areas under the two velocity curvesfrom 0 to t are the same, i.e at ca. t = 2.3.3.2The speed of a car (km/h) in a chase scene is given by the expressionv(t) = 2t 2 − 5t, 0 < t < 10where t is time in minutes. Use this expression to find(a) The acceleration over this time period.(b) The total displacement over the same time period.Solution(a) Acceleration a(t) = d dt v(t) = d dt (2t2 − 5t) = 4t − 5, for 0 < t < 10.(b) Total displacement over 0 < t < 10 is3.3x(10) − x(0) ==∫ 10∫ 10v(t) dt =00( ) 2t3 ∣∣∣∣3 − 5t2 102= 200030− 250 = 12503(2t 2 − 5t) dt= 2(1000)3− 5(100)2≈ 416.7 kmThe velocity of a boat moving through water is found to be v(t) = 10(1 − e −t ).(a) Find the acceleration of the boat and show that it satisfies a differential equation, i.e anequation of the form d[a(t)]/dt = −k · a(t) for some value of the constant k (i.e. find thatvalue of k).(b) Find the displacement of the boat at time t.Solution(a) The acceleration of the boat isa(t) = dv(t)dt= 10e −t 2

at any time t = T, up to and including the time when the car comes to a halt. Thereforev(0) − v(T )100 × 1000T = . The initial velocity is v(0) = = 1000 m/sec, and so the time860 × 60 36100036it takes the car to stop, once the brakes are applied, is T =− 0 ≈ 3.47 sec. Adding on8the reaction time, we see it takes 3.47 sec + 0.5 sec = 3.97 sec for the car to come to a fullstop.3.7You are driving your car quickly (at speed 100 km/hr) to catch your flight to Hawaii formid-term break. A pedestrian runs across the road, forcing you to brake hard. Suppose ittakes you 1 sec to react to the danger, and that when you apply your brakes, you slow downat the rate a = −10 m/sec 2 . How long will it take you to stop? How far will your car movefrom the instant that the danger is sighted until coming to a complete stop?SolutionLet t = 0 be the time you hit the brakes, and t = T be the time that you stop.100 kmYour velocity at t = 0 is · 1000 mh 1 km · 1 h3600 s = 1000 m36 s .The total time to stop is the sum of the following times: (1 sec reaction time) + (time toslow down from 1000 → 0 m).36 sThe velocity is related to acceleration by:∫ ∫v(t) = a dt = (−10) dt = −10t + CAt time t = 0, v(0) = 100036m/s, so C = 100036andv(t) = −10t + 100036 .To find the time to slow down from 1000 m/s to 0m/s, we set t = T and v(T ) = 0, which36gives 1000100− 10T = 0 ⇒ T = sec ≈ 2.8 sec.36 36 (Therefore, the total time to stop is 1 + 100 )sec ≈ 3.8 sec.36The(total distance traveled is equal to the following sum:1 sec at 1000 ) (36 m/s + distance traveled in T = 100)36 sec after brakingTo find the distance traveled after braking, we use the distance function (in meters), whichis related to velocity by:∫∫ (d(t) = v(t) dt = −10t + 1000 )36dt = −5t 2 + 100036 t + C5

3.9In ancient Egypt, most of the population was confined to the shores of the river Nile. Thedensity of the population decreased with increasing distance from the sea. Suppose that thepopulation density at distance x from the mouth of the river was p(x) = 200e −0.001x peopleper km, where x is distance in km.(a) What was the total population size along the first 100 km of the river?(b) What was the total population size along the whole length of the river?Solution(a) Let P (100) be the number of people that lived along the first 100 km. ThenP (100) =∫ 1000p(x) dx =∫ 1000100∣0200e −0.001x dx200=−0.001 [e−0.001x ] = 200 [e −0.001·100 − 1 ]−0.001= 200000[1 − e −0.1 ] = 19032.52 ∼ 19033 [people](b) Let P (L) be the number of people that lived along the entire length of the river. ThenP (L) =∫ L0p(x)dx =∫ L0200e −0.001x dxP (L) = 200−0.001 (e−0.001×L − 1).As L → ∞, e −0.001L → 0. So P (L) = 200 (−1) = 200000.−0.0013.10The air density h meters above the earth’s surface isp(h) = 1.28e −0.000124h (kg/m 3 )Find the mass of a cylindrical column of air 4 meters in diameter and 25 kilometers high.Let H = 25km = 25000m be the height, and let A = 1.28, a = −0.000124.SolutionThe total mass is M = 4π ∫ H0 p(h) dh = 4π ∫ ∣H∣∣∣0 Ae−ah dh = 4πA( e−ah ) H−a0123873.71kg.= 4πA 1−e−aH−a=7

3.11A test-tube contains a solution of glucose which has been prepared so that the concentrationof glucose is greatest at the bottom and decreases gradually towards the top of the fluid.(This is called a density gradient). Suppose that the concentration c as a function of thedepth x is c(x) = x/10 (in units of gm/cm 3 ). The radius of the tube is 2 cm 2 and the heightof the glucose-containing solution is 10 cm. Determine the total amount of glucose in thetube (in gm).SolutionAssume a cylindrical tube and consider slicing it along its axis. The volume of such a sliceis πr 2 ∆x, and this small slice contains an amount πr 2 ∆x · c(x) of glucose. The integral wewant is3.12∫ 10∫ 10C = πr 2 c(x) dx = πr 2 (x/10)dx = (4π/10)(x 2 /2)| 10000= 20π gm.Suppose a lake has a depth of 40 meters and is bowl-shaped, with the surface of the bowlgenerated by rotating the curve z = x 2 /10 around the z-axis. Here z is height in metersfrom the bottom of the bowl. The distribution of sediment in the lake is stratified by heightalong the water column. In other words, the density of sediment (in mass per unit volume)is a function of the form s(z) = C(40 − z), where z is again vertical height in meters fromthe point at the bottom of the lake. Find the total mass of sediment in the lake. (Youranswer will have the constant C in it.)SolutionThe radius of a horizontal slice through the lake at height z is x = √ 10z. The volume of oneof these slices is then V = πx 2 ∆z = π10z∆z. Therefore, the amount of sediment containedin a layer at height z from the bottom isThe total amount of sediment is therefore∫ 400s(z) · V = s(z) · π10z∆z = 10πC(40 − z)z∆z.10πC(40 − z)z dz = [10πC(20z 2 − z33 )] ∣ ∣∣∣ 400≈ 335103C [mass units].8

3.13Rates of change and total changeThe growth rate of two children (in gm/day) is shown in Figure 3. Suppose both have thesame weight at time t = 0.Figure 3: For problem 3.13(a) Which one is larger after 6 months?(b) Which one is larger after 1 year?SolutionThe size (e.g. weight) of each child is represented by the area under the growth curve up tothe given time.(a)After 6 months (0.5 year) the top growth curve has largest accumulated area. (The largestchild)(b)After 1 year, the area under the second curve has overtaken the area under the first. (Thesecond child has gotten larger that the first.)3.14The flow rate of blood through the heart can be described approximately as a periodicfunction of the form F (t) = A(1 + sin(0.15t)), where t is time in seconds and A is a constantin units of cubic cm per second. (Thus, at time t, F (t) cubic cm of blood flow through theheart per second.) Find the total volume of blood that flows through the heart betweent = 0 and t = 1. (Express your answer in terms of A.)Solution9

If the rate of flow is F (t), then the total flow between times t = 0 and t = 1 is3.15I =∫ 10F (t)dt =∫ 10A(1 + sin(0.15t))dt1I = A(t − cos(0.15t)/0.15)∣0I = A(1 − cos(0.15)/0.15) − A(−1/0.15) = A(1.15/0.15 − cos(0.15)/0.15)During a gambling session lasting 6 hours, the rate of winnings at a casino in dollars perhour are seen to follow the formula w(t) = 2000t(1 − (t/6)). Find the total winnings duringthat whole session.SolutionThe total winnings are3.16∫ 60(2000t 1 − t ) ∣ ∣∣∣dt = 1000t 2 6− 2000 ∣ ∣∣∣ 660 18 t3 = 36000 − 24000 = 12000.0At time t, an intravenous infusion delivers a flow rate of y = 100(1 − t 3 ) cm 3 /hr, where t istime in hours. The infusion contains a drug at concentration 0.1 mg/cm 3 . Find the totalvolume of fluid and the total amount of drug delivered to the patient over a 1 hour periodfrom t = 0 to t = 1.SolutionThe total volume of fluid delivered isI =∫ 10y(t)dt =∫ 10100(1 − t 3 )dtI = 100(t − t 4 /4)| 1 0 = 75 cm3 .The total amount of drug delivered is 0.1 mg/cm 3 · 75 cm 3 = 7.5 mg.3.17Oil leaks out of an oil tanker at the rate f(t) = 10 − 0.2t 2 (where f is in 10 thousand barrelsper hour and t is in hours). (Note: This function only makes sense as long as f(t) ≥ 0 sincea negative flow of oil is meaningless in this case.)(a) At what time will the flow be zero?10

(b) What is the total amount that has leaked out between t = 0 and the time you found in(a)?Solution(a) The flow will be zero when f(t) = 0, i.e. 10 − 0.2t 2 = 0 ⇒ t 2 = 50 at t = 5 √ 2 [hr].(b) The total amount of oil that has leaked out between t = 0 and t = 5 √ 2 is found as:3.18F (t) = (10t − 0.23 t3 )∣F (5 √ 2) − F (0) =5 √ 20∫ 5√20f(t) dt =∫ 5√20(10 − 0.2t 2 ) dt= 50 √ 2 − 0.2 × (5 √ 2) 3 /3 = 47.14 × 10 thousand barrels.After a heavy rainfall, the rate of flow of water into a lake is found to satisfy the relationship( ) t 2F (t) = 4 −10 − 1 where t is time in hours, 0 < t < 30 and F is in units of 100,000gallons/hr.(a) Find the time, t 1 at which the rate of flow is greatest.(b) Find the time, t 2 at which the flow is zero.(c) Find how much water in total has flowed into the lake between these two times.Solution( ) t(a) F ′ (t) = −210 − 1 × 110 = 0 ⇐⇒ t = 10. Since F ′′ (t) = − 1 < 0 this value of t gives50the maximum rate of flow.( ) t 2(b) The flow is zero when F (t) = 0, ie. 4 −10 − 1 = 0 ⇒ t 2 = 30.(c) The total water flowing into the lake between these times is∫ ( 30 ( ) ) t 2 4 −10 10 − 1 30dt = 4t∣ − 10 ( ) t 3 ∣ ∣∣∣3 10 − 1 30= 160 × 100 000 gallons.33.1910The growth rate of a crop is known to depend on temperature during the growing season.Suppose the growth rate of the crop in tons per day is given by g(t) = 0.1(T (t) − 18) whereT (t) is temperature in degrees Celsius. Suppose the temperature record during the 90 daysof the season was T (t) = 22 + 0.1t + 4 sin(2πt/60) where t is time in days. Find the totalgrowth (in tons) that would have occurred over the whole season.Solution1110

The total growth of crop in 90 days is given as:G(90) − G(0) =∫ 900g(t) dt =∫ 900(0.1(T (t) − 18)) dt∫ 90G(t) = 0.1 (22 + 0.1t + 4 sin(2πt/60) − 18) dt = 0.1(4t + 0.102 t2 − 4 · 60∣ ∣∣∣2π cos(2πt/60)) 900G(t) = 0.1(360 + 405 − 120 (cos(3π) − cos(0))) = 0.1(765 + 240/π) = 84.1394 tonsπ3.20This question concerns cumulative exposure to radiation experienced by people living nearnuclear waste disposal sites.(a) Recall from last term that radioactive material decays according to a negative exponential:m(t) = m 0·e −rt , where m(t) is the mass of the radioactive material at time t, m 0 = m(0)is the initial mass at time t = 0, and r is the rate of decay. The half-life is the time it takesfor the material to decay to one half its initial mass. Suppose that t is measured in months.Determine the rate of decay r if the half-life is 1 month.(b) Assume that at any time, the amount of radiation is proportional to the mass of theradioactive material. If initially the radiation level is 0.5 rads per month, how could wedescribe the radiation level as a function of time?(c) Assume now that there is radioactive material in your backyard of the type consideredin (a) above, i.e. that it has a half-life of one month. Calculate the cumulative exposure inrads that would occur if you lived in your house for 10 years.Solution(a) Since the half-life is 1 month, t = 1, and we get from the formula for m(t): m o /2 =m o e −r ⇒ 0.5 = e −r ⇒ r = ln(2).(b) The amount of radiation R(t) is proportional to the mass of radioactive material. Nowwe know from (a) thatm(t) = m o e − ln(2)t .So,And finally, R(t) ≈ 0.5e −ln(2)t [rads].R(t) ≈ m(t) = m o e − ln(2)t ,0.5 = R(0) ≈ m o e − ln(2)×0 = m o .(c) Cumulative exposure in 10 years (120 months) is:∫ 12000.5e ln(2)t dt = 0.5− ln(2) e− ln(2)t ∣ ∣∣∣ 1200= 0.5ln(2) (1 − e−120 ln(2) ) = 0.7213 [rads].12

Figure 5: For problem 3.22In a short time interval dt, amount flowing in is I(t) dt, amount flowing out is O(t) dt, andthe total change is I(t) dt − O(t) dt = [I(t) − O(t)] dt.(a) Let Q(t) be the total amount of water, t = 0 corresponds to start of the year.Q(T ) − Q(0) = total change over interval [0, T ] = sum of small changes = ∫ T0 [I(t) − O(t)] dt(b) Maxima and minima occur at critical points Q ′ (t) = 0. By the Fundamental Theoremof Calculus, Q ′ (t) = I(t) − O(t). Now Q ′ (t) = 0 ⇒ I(t) = O(t).At critical point A (see Figure 6), if t < A, I(t) > O(t) ⇒ Q ′ (t) > 0 ⇒ Q increases.For A < t < B, O(t) > I(t) ⇒ Q ′ (t) < 0 ⇒ Q decreases.Hence, A is the maximum, B is the minimum.Figure 6: For problem 3.22 solution3.23The rate at which animals migrate into and out of a wildlife reserve is described by twofunctions shown in Figure 7. I(t) is the rate at which animals enter the reserve and O(t) isthe rate at which they leave (both in number per day).(a) Express the number of animals in the reserve as a definite integral.(b) When is the number of animals in the reserve greatest and when is it smallest?Solution14

££££££££££££££££££££££££f(x)f*¡¡¡¡¡¡¡¡¡¡¡¢¡¢¡¢¡¢¡¢¡¢¡¢¡¢¡¢¡¢¡¢¡¢¡¢¡01x3.25Figure 9:During a particularly soggy week in Vancouver, rainfall reached epic proportions. The rainfallpattern was as follows: A constant 20mm on the first 24 hrs, a steady increase from 20 upto 50 mm over the next 24 hrs (assume linear increase), 50mm rain over the next 24 hrs, asteady drop from 50 down to 40 mm over the next 24 hrs, and a flat 30 mm over the next24 hrs. Determine the total amount of rain during this period and the average daily rainfallfor the same period.SolutionSee Figure 10.5rainfall (in cm)4321constant rate20mm/dayA2A1A3A4A51 2 3 4 5daysFigure 10: For problem 3.25 solutionTotal amount of rain = A 1 + A 2 + A 3 + A 4 + A 5= (2 + 7 2 + 5 + 9 5 + 3)16

= 18 cmAverage rainfall over 5 days =18 cm total5 days= 3.6 cm/day.3.26 [98 Final]Find the average value of the function f(x) = sin( πx ) over the interval [0,2].2Solution3.27¯f = 1 ∫ 2sin2 − 0 0( ) πxdx = 1 2 2( ) [ −2cosπ(a) Find the average value of x n over the interval [0, 1].( )] ∣ πx ∣∣∣ 2= −12 0 π (−1 − 1) = 2 π(b) What happens as n becomes arbitrarily large (that is, n → ∞)?(c) Explain your answer to part (b) by considering the graphs of these functions.(d) Repeat parts (a) - (c) using the functions x 1/n .Solution(a) Let f(x) = x n ,f avg = 1 ∫ 1x n dx = xn+11∣1 − 0 0 n + 1 0(b) As n → ∞, f avg → 0.= 1 , for n ≠ −1n + 1(c) See Figure 11.As n → ∞, the area under the curve in the interval [0, 1] gets smaller and smaller.(d) Let g(x) = x 1/n ,g avg = 1 ∫ 1x 1/n dx = x1/n+11∣ = 11for n ≠ −11 − 0 01/n + 1 0 + 1,nAs n → ∞, g avg → 1. See Figure 12.As n → ∞, the area under the curve in the interval [0, 1] gets closer to 1.17

yyy = xy = x 21x1xyyy = x 3y = x 41x1xFigure 11: For problem 3.27 (c) solutionyyy = xy = x 1/21x1xyyy = x 1/3y = x 1/41x1xFigure 12: For problem 3.27 (d) solution18

3.28An object starts from rest at t = 0 and accelerates so that a = dvdt = ce−t where c is a positiveconstant.(a)Find the average velocity over the first t seconds.(b)What happens to this average velocity as t becomes very large?Solutiona = dv = ce −t . v(0) = 0 since the object starts from rest. v = ∫ ∣t∣∣∣dt0 ce−t dt = −ce −t t0−c(e −t − e−0) = c(1 − e −t ) Therefore, velocity at anytime t is v(t) = c(1 − e −t )(a) Average velocity after first t seconds:∫1 tv(s) ds = 1 ∫ tt 0t c (1 − e −s )ds0= c t (s + te−s )∣0= c t (t + e−t − 0 − e −0 )= c t (t + e−t − 1)== C(1 + e−tt− 1 t )(b)When t → ∞, average velocity → C3.29 Symmetry(a) Find the average value of the function sin x over the interval [−π, π].(b) Find the average value of the function x 3 over the interval [−1, 1].(c) Find the average value of the function x 3 − x over the interval [−1, 1].(d) Explain these results graphically.(e) Find the average value of an odd function f(x) over the interval [−a, a]. (Remember thatf(x) is odd if f(−x) = −f(x).)(f) Suppose now that f(x) is an even function (that is, f(−x) = f(x)) and its average valueover the interval [0, 1] is 2. Find its average value over the interval [−1, 1].Solution(a)∫1 πsin x dx = 1 ∣ ∣∣∣π − (−π) −π 2π (− cos x) π= − 1 (1 − 1) = 0−π 2π19

yy = sin xyy = x 3−π π X−1 1 Xyy = x 3 −x−1 1XFigure 13: For problem 3.29 (e) solution(b)∫1 1x 3 dx = 1 1 − (−1) −1 2x 441∣ = 1 (1 4 − (−1) 4) = 0−1 8(c)∫1 11 − (−1) −1(x 3 − x) dx = 1 2( x44 − x22) ∣∣∣∣ 1= 1 ( 1−1 2 4 − 1 2 − 1 4 + 1 )= 02(d) See Figure 13. All these graphs are symmetric about the origin, so that the integral∫ 0−π sin x dx = − ∫ π0 sin x dx and they cancel out (similarly for the other two functions).(e) Odd function (symmetric about the origin): f(−x) = f(x).∫1 af(x) dx = 1 ∫ af(x) dx = 1 [∫ 0∫ a ]f(x) dx + f(x) dxa − (−a) −a 2a −a 2a −a0Now, let x = −u, then dx = −du, x = −a ⇒ u = a etc.∫ 0−af(x) dx = −= −== −∫ 0a∫ 0a∫ 0a∫ af(−u) du(−f(u)) du ⇒ since f is oddf(u) du = −0∫ a0f(u) du reversing limits of integrationf(x) dx since u is just a “dummy ′′ variable of integration20

Therefore,∫ 0−af(x) dx +∫ a0∫ a∫ af(x) dx = − f(x) dx + f(x) dx = 000Thus, the average value of an odd function over a symmetric interval [−a, a] is 0.(f) We are given that f(x) is an even function (that is, f(−x) = f(x)) and its average valueover the interval [0, 1] is 2. This means that¯f [0,1] = 1 1∫ 10f(x) dx =The average value over the interval [−1, 1] is¯f [−1,1] =∫ 10f(x) dx = 2∫1 1f(x) dx = 1 ∫ 1∫ 1(1 − (−1)) −1 2 · 2 f(x) dx = f(x) dx = ¯f [0,1]00(We have used the symmetry of the function here: the definite integral of an even functionover a symmetric interval about the y-axis will be double the value of the definite integralover half that interval.) Thus¯f [−1,1] = ¯f [0,1] = 2.3.30The intensity of light cast by a street lamp at a distance x (in meters) along the street fromthe base of the lamp is found to be approximately I(x) = 20 − x 2 in arbitrary units for−20 < x < 20.(a) Find the average intensity of the light over the interval −5 < x < 5.(b) Find the average intensity over −7 < x < 7.(c) Find the value of b such that the average intensity over [−b, b] is I av = 10.SolutionThe intervals and the function are symmetric, so∫1 aI av =(20 − x 2 ) dx = 1 ∫ aa − (−a) −a2a (2) (20 − x 2 ) dx = 1 ( ) ∣∣∣∣20x − x3 a0a 3 0(a) I av = 1 ∫ 55 0 (20 − x2 ) dx = 1 53[100 − ] = 35.5 3 3(b) I av = 1 ∫ 77 0 (20 − x2 ) dx = 1 73[140 − ] = 11.7 3 3(c) Solve 10 = 1 ∫ bb 0 (20−x2 ) dx for b. Integrating the right hand side gives 1[20b− b3 ] = 20− b2 .b 3 3Setting this equla to the left hand side gives b = √ 30 ≈ 5.477 meters.21

3.31The length of time from sunrise to sunset (in hours) t days after the Spring Equinox is givenby( ) πtl(t) = 12 + 4 sin182(a) Explain the meaning of the word “Equinox” and describe what happens on that dayaccording to the above formula.(b) What is the length of the shortest and the longest day and when do these occur accordingto this formula?(c) How long is one complete cycle in this expression?(d) Sketch l(t) as a function of t.(e) Find the average day-length over the month immediately following the Equinox.(f) Find the average day length over the whole year.geometric or intuitive argument.Solution( ) πtl(t) = 12 + 4 sin182Explain your result with a simple(a) Equinox is a time of year when the length of “day” (sunrise → sunset) equals the lengthof “night” (sunset → sunrise). This happens twice a year, once in spring and once in fall.On the Equinox, l(t) = 12 hours( ) πt⇒ 12 = 12 + 4 sin182⇒ t = 0 (Spring Equinox) or t = 182 (Fall Equinox)(b) We know that −1 ≤ sin ( ) ( )πt182 ≤ 1. So the longest day will occur when sin πt182 = 1 andthe shortest day will occur when sin ( )πt182 = −1.Longest day( ) πtsin = 1 ⇒ πt182 182 = π 2 ⇒ t = 91l(91) = 12 + 4 · 1 = 16 hours, occurs 91 days after the Spring Equinox.Shortest day( ) πtsin = −1 ⇒ πt182 182 = 3π 2 ⇒ t = 27322

l(273) = 12 + 4(−1) = 8 hours, occurs 273 days after the Spring Equinox.(c) One complete cycle is 2(182) = 364 days, from this expression:sin(ωt) has frequency ω ⇒ ω cycles in every 2π.Therefore the length of one cycle = 2π ω = 2ππ/182 = 364.(d) See Figure 14.161412Spring EquinoxFall Equinox10l(t)hours864200 91 182 273 364tdaysFigure 14: For problem 3.31 (d)(e) Average day-length over 1st month after Spring Equinox (assume 30 days in month):l avg = 1 ∫ 30l(t) dt = 1 ∫ 30 (( )) πt12 + 4 sin dt30 0 30 0182= 1 (12t − 4 · 182 ( )) ∣ πt ∣∣∣ 30cos30 π 182 0= 1 [12 · 30 − 4 · 182 ( ) π · 30cos + 4 · 182 ]cos 030π 182 π= 12 − 364 ( ) 15π15π cos + 364 ≈ 13 hours91 15π(f) Average day length over whole year: (expect ≈ 12 hours)l avg = 1 ∫ 365l(t) dt365 0= 1365(12t − 4 · 182π( πtcos182)) ∣ ∣∣∣ 3650( π · 365182= 1 [12 · 365 − 4 · 182 cos365π= 12 − 728 ( ) 365π365π cos + 728182 365π= 12.0009 (≈ 12, as expected))+ 4 · 182 ]πFrom the graph in (d), we can see that over 364 days (almost a year) the average value ofl(t) is 12 hours.23

3.32Consider the periodic function,f(t) = sin (2t) + cos (2t)(a) What is the frequency, the amplitude, and the length of one cycle in this function?Consider A sin(ωt + ϕ), A = amplitude, ϕ = phase shift, ω = frequency.A sin(ωt + ϕ) = A(sin(ωt) cos ϕ + cos(ωt) sin ϕ)(b) How would you define the average value of this function over one cycle ?(c) Compute this average value and show that it is zero. Now explain why this is true usinga geometric argument.Solution(a) Consider A sin(ωt + ϕ), A = amplitude, ϕ = phase shift, ω = frequency.If ϕ = π 4A sin(ωt + ϕ) = A(sin(ωt) cos ϕ + cos(ωt) sin ϕ)and ω = 2, thenA sin(2t + π 4 ) = A (sin(2t) ·)11√ + cos(2t) · √2 2If A = √ 2, then√ π 2 sin(2t + ) = sin(2t) + cos(2t) = f(t)4Therefore, frequency ω = 2 (meaning 2 cycles in length 2π), amplitude A = √ 2, length ofone cycle = 2π/2 = π.(b) Average value of f(t) over one cycle:(c)f avg =1(length of cycle)∫ length0f(t) dt = 1 πf avg = 1 [− cos(2t) + sin(2t) ] ππ 2 20= 1 [(− 1 )π 2 + 0 −(− 1 )]2 + 0= 0∫ π0(sin(2t) + cos(2t)) dt(cos(2π) = 1, cos 0 = 1, sin(2π) = 0, sin 0 = 0.)See Figure 15. Over one cycle, there is equal amount of area above the x-axis as below thex-axis, so the average value of the function over one cycle is 0.24

2 1/2−π/8Figure 15: For problem 3.323.33The current in an AC electric circuit is given byI(t) = A cos(ωt)The power in the circuit is defined as P (t) = I 2 (t).(a) What is meant by one cycle in this situation?(b) Sketch graphs of I(t) and P (t). Explain why P (t) is always positive, and indicate howits zeros are related to zeros of I(t). What are the maximal and minimal values of each ofthese functions?(c) Find the average power and the average current over half a cycle. (Note: in computingthe average power, you will need to use the trick cos 2 (ωt) = 1 (1 + cos(2ωt))).2Solution(a) One cycle in this situation is one period (max to max or min to min) in the currentfunction I(t) = A cos(ωt).The frequency is ω so the period (i.e. the length of one cycle) is 2π ω .This length is equivalent to two periods (but one cycle) of the power function. The power isusing double-angle formula.( )1 + cos(2ωt)P (t) = I 2 (t) = A 2 cos 2 (ωt) = A 2 2P (t) = A22(b) See Figure 16.P (t) ≥ 0 since it is the square of I(t).(1 + cos(2ωt))25

I(t)P(t)AA 2 π / ω t2π / ωt−AFigure 16: For problem 3.33I(t) = 0 ⇒ cos(ωt) = 0⇒ ωt = π 2 , 3π2 , . . .⇒ t = π2ω , 3π2ω , . . .P (t) = 0 ⇒ I 2 (t) = 0 ⇒ I(t) = 0⇒ t = π2ω , 3π2ω , . . .Therefore, I(t) and P (t) have the same zeroes.Maximal and minimal values: −A ≤ I(t) ≤ A, 0 ≤ P (t) ≤ A 2 .The amplitude of I(t) is A, and thus it fluctuates between a maximum of A and a minimumof −A.Because P (t) is the square of I(t), it must always be greater than 0, which is therefore itsminimum. Its maximum is A 2 , the square of the amplitude of I(t).(c) Average power over a half cycle: (cycle length is 2π ω )P avg = ω π= ω π= ωA22π= ωA22π∫ π/ω0∫ π/ω0[P (t) dt = ω πA 22∫ π/ω(1 + cos(2ωt)) dtt + sin(2ωt)2ω0[ ] πω + 0 − 0 = A22 watts0] π/ωI avg = ω πA 2 cos 2 (ωt) dt∫ π/ω026I(t) dt

= ω π∫ π/ω0A cos(ωt) dt= ωA ∣ π∣∣∣πω sin(ωt) ω= A (0 − 0) = 0π0watts, as expected.27