Raffles Institution 2011 Year 6 Preliminary ... - ASKnLearn

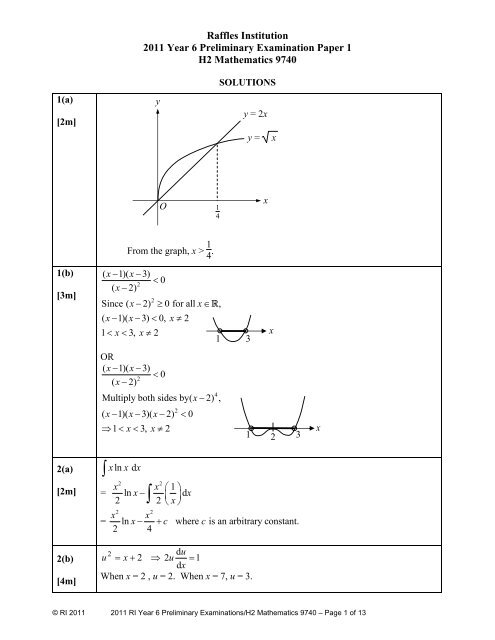
Raffles Institution2011 Year 6 Preliminary Examination Paper 1H2 Mathematics 97401(a)[2m]ySOLUTIONSy = 2xy = xO 14x1(b)[3m]2(a)[2m]2(b)[4m]From the graph, x > 1 4 .( x−1)( x−3)< 02( x − 2)2Since ( x−2) ≥0 for all x∈R,( x−1)( x− 3) < 0, x≠21< x< 3, x≠2OR( x−1)( x−3)< 02( x − 2)4Multiply both sides by( x − 2) ,2( x−1)( x−3)( x− 2) < 0⇒ 1< x< 3, x≠2∫x ln x dx∫1 32 2x x ⎛1⎞= ln x − ⎜ ⎟dx2 2 ⎝ x ⎠2 2x x= ln x− + c where c is an arbitrary constant.2 42duu = x + 2 ⇒ 2u = 1d xWhen x = 2 , u = 2. When x = 7, u = 3.x1 3 2x© RI 2011 2011 RI Year 6 Preliminary Examinations/H2 Mathematics 9740 – Page 1 of 13

Since Pkis true implies Pk + 1is true, and P1is true, by mathematical induction, Pnis+true for all n ∈Z .n n + 1The series converges as ( −1) → 0 when n →∞, which impliesn!n n + 1( −1) −1→− 1 when n →∞.n!Hence the sum to infinity is − 1.4(a)[3m]xLet y =−1sin 3( x)−1⎛ 3 ⎞sin (3 x)− x2dy⎜⎟1−9x=⎝ ⎠2dxsin 3−1( ( x))=2 −11−9x sin (3 x) −3x−( ( x))122sin 3 1−9x(b)[4m]5[7m]ycos 2x3=xTaking ln on both sides,( )( )cos 2x ln y = ln x = 3ln x3Differentiate w.r.t. x,1dy3( − 2sin 2x)( ln y) + ( cos 2 x)= ........... (1)y d x xcos 2π3 3At x= π,y = π ⇒ y = πSubst into (1):31 dy3( − 2sin2π)( lnπ ) + ( cos2π)=3π dxπdy2∴ = 3πdxy = e− 1tan 2xDifferentiate w.r.t. x,dy2= e2dx1 + 4xdy1+ 4 = 2ydx2( x )− 1tan 2x© RI 2011 2011 RI Year 6 Preliminary Examinations/H2 Mathematics 9740 – Page 3 of 13

Differentiate w.r.t. x again,2( x )dy d y dy8x+ 1+ 4 = 22dxdxdx22 d y( x ) ( x)2dy∴ 1+ 4 = 2 1−4 (shown)2dxdxWhen x = 0,2− 1tan 0y = e = 1dy= 2dxd y= 22( 2)= 4dx⎛ 2x ⎞∴ the Maclaurin's series of y is 1+ 2x+ 4 + ...⎜2 ⎟⎝ ⎠2= 1+ 2x+ 2 x + ...− 1tan 2xe 1 − 1etan 2x⎛ 1−1x ⎞= ⎜ + ⎟(2 + x) 2 ⎝ 2 ⎠21 2⎛ x x ⎞= ( 1 + 2 x+ 2 x + ... ) ⎜ 1 − + + ... ⎟2 ⎝ 2 4 ⎠21 ⎛ 1 2 22 x 2 x ⎞= ⎜ + x+ x − − x + + ... ⎟2⎝2 4 ⎠1 3 5 2= + x+ x + ...2 4 86(i)[1m]Usingak2k−1⎛a1⎞= ⎜ ⎟3⎝ 3 ⎠, we havea33−12⎛1⎞1= 3 ⎜ ⎟ = .⎝3⎠276(ii)[3m]6(iii)[2m]22Area of rectangle with base ( ak− ak + 1)and height ak + 1is ( ak − ak+ 1)( ak+1).2akUsing the recurrence ak + 1= we have32( ak − ak+ 1)( ak+ 1) = ( ak − ak+ 1)(3 ak+2). So ( ak − ak+ 1)(3 ak+2)© RI 2011 2011 RI Year 6 Preliminary Examinations/H2 Mathematics 9740 – Page 4 of 13n∑k = 1represents the sum of the areas of rectangles under the curve y = x 2 from a n + 1 to1. This is clearly less than the exact area under the curve y = x 2 from 0 to 1 =12 1∫x dx=and hence we have0 3nn1 1∑( ak − ak+ 1)(3 ak+ 2) < ⇒∑( ak − ak+ 1)( ak+2) < .3 9k= 1 k=1n∑k=1nn2 2 −1⎛1⎞ ⎛1⎞( ak − ak+ 1) = a1− an+1 = 1− 3⎜ ⎟ = 1−⎜ ⎟⎝3⎠ ⎝3⎠

6(iv)[2m]7(i)[2m]7(ii)[5m]n2⎛1⎞3 3Since a n = ⎜⎝ ⎟⎠Therefore,−11, the sequence is decreasing and thus, an≤ a3= for n ≥ 3.27n n n∑ ∑ ∑( a − a ) a < ( a − a ) a = a ( a −a)k k+ 1 k+ 2 k k+ 1 3 3 k k+1k= 1 k= 1 k=1n1= ∑ ( ak−ak+1)27k = 1n2 11 ⎛−⎛1⎞⎞ 1= 1 − < .27 ⎜⎜ ⎟⎝3 ⎠ ⎟ 27⎝ ⎠1dy=∫ 1 1 + ( y −ln2)22 1 −( y −2)1 −( y −2)2+ c = 1 y −ln12 3−y2x2 xy = 2 + ⇒ ( y − 2) =222 + x2 + x2( y− 2) + x ( y− 2) = xx2 2 2 222( y − 2)=1 − ( y − 2)2+ c2=− 2 + where a =− 2 and b=221 −( y −2)1 7When x = , y = 2 37(iii)[2m]Volume required273⎛1⎞ ⎛7⎞ 2= π π ⌠ ⎮⎜ ⎟ ⎜ ⎟ − 2 dy22 3 ⎮⌡ − +⎝ ⎠ ⎝ ⎠ 1 −( y −2)=73⌠7π 2π ⎮⎮⎮⌡⎛ ⎞− ⎜− 2+dy2 ⎟12 ⎝ 1 −( y −2)⎠22= 7 π 72π ⎛ 2⎞7+ ⎜ − ⎟12 ⎝3⎠ − 312π ⌠ ⎮⎮⌡dy21 −( y −2)= 5 734 π − y 1π ⎡ −⎢ln ⎤⎥⎣ 3 − y ⎦ 2= 5 4 π − ⎛ 2 4⎟ ⎞⎜−ln + ln⎝ 3 3 ⎠π⎛5 ⎞= ⎜ − ln 2 ⎟π⎝4⎠Given0⌠⎮⎮⌡ k© RI 2011 2011 RI Year 6 Preliminary Examinations/H2 Mathematics 9740 – Page 5 of 1321⌠ 2⎮⎮⌡ 0⎛ x ⎞ ⎛ x ⎞2+dx= 2⎜2 ⎟⎜2+dx2 ⎟⎝ 2 + x ⎠ ⎝ 2 + x ⎠

⎡⎢2x+ 2+x⎣2⎤⎥⎦0k=2⎡⎢2x+ 2+x⎣2 − (2k + 2 + k ) = 5 − 2 22k + 2 + k = 3 2 − 5From G.C. k = − 1. 36 (to 3 s.f.)222⎤⎥⎦1208(a)(i)[1m]ddxd y3x 3x 3x( y ) y( )e = 3e + edx8(a)(ii) dy+ 3y= 1dx[2m] 3xMultiply both sides by e :3x dy3x 3xe + 3ye = edxBy integrating both sides,3x3xye= e dx∫3xe= + c31y = + c c3Alternatively,−3xe where is an arbitrary constant.dy+ 3y= 1dxdy= 1−3ydx1 dy= 11−3ydx1∫ dy=1 dx1−3y∫1− ln 1 − 3 y = x+A where A is an arbitrary constant.3ln 1− 3y =− 3( x+A)1− 3y= e−3x−3A−3A−3x1− 3y=± e e−3A−3x3y= 1∓e e1 −3x1 −3Ay= + ce where c=∓ e is an arbitrary constant.3 3© RI 2011 2011 RI Year 6 Preliminary Examinations/H2 Mathematics 9740 – Page 6 of 13

8(a)(iii)[3m]c > 0y1y =3x(c = 0)c < 08(b)[4m]dy2x y xdx = +Since y= vx, differentiate w.r.t. x ,dydv= v+xdxdx⎛ dv⎞∴ x⎜v+ x ⎟= vx+x⎝ dx⎠dv= 1dxv= x+cy= x+cx2y = x + cxWhen y = 5 when x = 1 , c = 4 .2The particular solution is y = x + 4x.29(i)[2m]Method 1⎛4⎞ ⎛−1⎞ ⎛2t⎞A vector perpendicular to π1is ⎜t⎟× ⎜ 0 ⎟= ⎜−9⎟.⎜1⎟ ⎜ 2 ⎟ ⎜ t ⎟⎝ ⎠ ⎝ ⎠ ⎝ ⎠⎛2t⎞ ⎛2⎞Since ⎜−9 ⎟ is parallel to ⎜3 ⎟,⎜ t ⎟ ⎜1⎟⎝ ⎠ ⎝ ⎠⎛2t⎞ ⎛2⎞⎜− 9⎟= m⎜3 ⎟ for some m∈R\{0}.⎜ t ⎟ ⎜1⎟⎝ ⎠ ⎝ ⎠⎧t= m⇒⎨ ⇒ m=− 3, t =−3.⎩ − 9 = 3m© RI 2011 2011 RI Year 6 Preliminary Examinations/H2 Mathematics 9740 – Page 7 of 13

Method 2⎛4⎞Since ⎜t⎟ is parallel toπ ⎜1⎟1,⎝ ⎠So 8+ 3t+ 1= 0 ⇒ t =− 3⎛4⎞ ⎛2⎞⎜t⎟i⎜3⎟=0⎜1⎟ ⎜1⎟⎝ ⎠ ⎝ ⎠9(ii)[3m]Method 3Take a point on π1,⎛2⎞ ⎛4⎞ ⎛6⎞e.g. the point with position vector ⎜0 ⎟+ ⎜t ⎟ = ⎜t ⎟ where λ = 1, μ = 0 .⎜1⎟ ⎜1⎟ ⎜2⎟⎝ ⎠ ⎝ ⎠ ⎝ ⎠⎛6⎞ ⎛2⎞Hence ⎜t⎟i ⎜3⎟=5 ⇒ 12 +3t + 2 = 5 ⇒ t = −3⎜2⎟ ⎜1⎟⎝ ⎠ ⎝ ⎠Method 1⎛ 6 ⎞ ⎛ 2 ⎞ ⎛ 4 ⎞AB = ⎜−3⎟−⎜− 9⎟=⎜ 6 ⎟⎜ s ⎟ ⎜14 ⎟ ⎜s−14⎟⎝ ⎠ ⎝ ⎠ ⎝ ⎠ 2Since AB ⊥ π1, ⎛ ⎞AB // ⎜3⎟⎜1⎟⎝ ⎠⎛ 4 ⎞ ⎛2⎞So ⎜ 6 ⎟= k⎜3 ⎟ for some k∈\{0}⎜s−14⎟ ⎜1⎟⎝ ⎠ ⎝ ⎠4= 2k⎫⎬ ⇒ k = 2, s = 16s− 14 = k⎭Method 2Since AB ⊥ π1, ⎛−1⎞ ⎛ 4 ⎞ ⎛−1⎞AB i⎜ 0 ⎟= 0, i.e. ⎜ 6 ⎟i⎜ 0 ⎟= 0 ⇒− 4+ 2s − 28= 0⇒ s = 16⎜ 2 ⎟ ⎜s−14⎟ ⎜ 2 ⎟⎝ ⎠ ⎝ ⎠ ⎝ ⎠Method 3Let N be the midpoint of AB.2 6 ⎛ 4 ⎞OA + OB 1⎡⎛ ⎞ ⎛ ⎞⎤ON = 2 = 2 ⎢⎜− 9⎟+ ⎜− 3⎟⎥= ⎜ −6⎟⎢⎜ 14 ⎟ ⎜ s ⎟⎥ ⎜7 1s⎟⎣⎝ ⎠ ⎝ ⎠⎦ ⎝ +2 ⎠Since midpt of AB, N, lies on π 1 ,⎛ 4 ⎞ ⎛2⎞⎜1− 6 ⎟i⎜3⎟= 5 ⇒ 8-18+7+ s = 5 ⇒ s = 162⎜ 17 + s⎟ ⎜1⎟⎝ 2 ⎠ ⎝ ⎠#© RI 2011 2011 RI Year 6 Preliminary Examinations/H2 Mathematics 9740 – Page 8 of 13

9(iii)[3m]The point B lies on line l and since π2contains l and pt A, so A and B lie on π2.Since AB lies on π2and AB ⊥ π1(as A is obtained by reflecting B in π1OR⎛2⎞AB //3, i.e. AB is parallel to a normal vector of π1), hence π1 ⊥ π2.⎜1⎟⎝ ⎠ORA normal vector of π 2 , n 2 3 4 3 4 2= AB× ⎛ − 2 ⎞ = ⎛ 6 ⎞ × ⎛ − 2 ⎞ = ⎛ 6 ⎞ = 2 ⎛ 3⎞⎜ 0 ⎟ ⎜2⎟ ⎜ 0 ⎟ ⎜−26⎟ ⎜−13⎟⎝ ⎠ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠⎛2⎞A normal vector of π 2 , n 1 =3⎜1⎟⎝ ⎠⎛ 2 ⎞ ⎛2⎞Since ⎜ 3 ⎟i⎜3⎟= 4 + 9 − 13 = 0 ⇒ n1 ⊥n2⇒ π1 ⊥π2#⎜−13⎟ ⎜1⎟⎝ ⎠ ⎝ ⎠Method 1⎛2⎞Equation of π1is r i3⎟=5⎜1⎟⎝ ⎠Since A and B lie on π2, and AB ⊥ π1, hence π1 ⊥ π2.Shortest distance from A to intersection line= Perpendicular distance from A to π11 12 AB 22 2 2( )= = 2 2 + 3 + 1 = 14 unitsMethod 2Take a point on π1 , e.g. C(2, 0, 1).Shortest distance from A to intersection line= Perpendicular distance from A to π1 ⎛2⎞ ⎛ 0 ⎞ ⎛2⎞AC i ⎜3⎟ ⎜ 9 ⎟ i ⎜3⎟⎜1⎟ ⎜ 13⎟ ⎜1⎟⎝ ⎠ ⎝−⎠ ⎝ ⎠ 27 −13= = = =⎛2⎞ 2 2 22 + 3 + 1 14⎜3⎟⎜1⎟⎝ ⎠14 units© RI 2011 2011 RI Year 6 Preliminary Examinations/H2 Mathematics 9740 – Page 9 of 13

10(i)[3m]1 3 2y= ( x − 39x + 399 x), so10dy3 23( x 26x 133) ( x 7)( x 19 ).dx = 10 − + = 10− −Thus d y0dx = when x = 7 or x = 19, and the stationary points are( 7,122.5 ) and ( 19,36.1 ).d y 3dy222( x 13 ),dx = 5− so 02dx < at ( 7,122.5 )2and 02dx > at ( 19,36.1 ).Thus ( 7,122.5 ) is a maximum point and ( 19,36.1 ) is a minimum point.dy10(ii)[2m]y( 7,122.5)1 (2 39 399)y= x x − x+10( 19,36.1)Ox10(iii)[2m]y( 7, + 122.5)( 19, + 36.1)O( 19, − 36.1)x( 7, − 122.5)1= ( − 39 + 399)102 2y x x x10(iv) The volume of water in the vase when the depth is h , V , is given by© RI 2011 2011 RI Year 6 Preliminary Examinations/H2 Mathematics 9740 – Page 10 of 13

[4m]11(a)[2m]π h3 2V = ( x − 39x + 399x)d x,10∫ so0dVd⎡ππ39 399 d 39 399 .⎦3 2 ⎤3 2( x − x + x) x = ( h − h + h)h=dhdh⎢10∫ 0⎥ 10⎣Since d V d V d h= , we havedt dh dtdh dV dV=dtdtdh10 100= π =π − +103 2( h) ( )3 − 39h2 + 399hh 39 h 399 hWhen h = 19 we get d h= 100 = 0.0882 (3 s.f.).dt361πyy = e 2x x− 2e.O ln 2xy = k−1(i)[1m](ii)[2m](b)[6m]Range of f, R f = [−1,∞).Since the line y = k (−1 < k < 0) does not intersect the graph of y = f(x) at one and onlyone point, f is not one - one.Hence f −1 does not exist.gf(x) = e 2ln3x − 2e ln3x = e ln(3x)2 − 2(3x) = 9x 2 − 6x.Let y = e 2x x− 2e⇒ y = (e x − 1) 2 − 1 (a = 1, b = 1)⇒ x = ln ( 1 − y + 1 ) or ln ( )⇒ h −1 (x) = ln ( 1 − x + 1 ).∴ h −1 : x ln ( 1 − x + 1 ), x ∈ , −1 ≤ x < 0.1 + y + 1 ( rejected, since x ≤ 0 ) .© RI 2011 2011 RI Year 6 Preliminary Examinations/H2 Mathematics 9740 – Page 11 of 13

12(a)[3m]zz55− 16(1 + 3 i) = 0= 16(1 + 3 i)πi5 3= 2e⎛π⎞i 2kπ5⎜ + ⎟⎝3⎠= 2e , k ∈Z⎛ π 2kπ⎞i ⎜ + ⎟⎝15 5 ⎠⇒ z = 2e , k = −2, −1, 0, 1, 2.12(a)[2m]Let11 13−π i −π i π i 7π i π i15 3 15 15 151= 2e ,2= 2e ,3= 2e ,4= 2e ,5= 2ez z z z z3,−1)P 5 (z 5 )P 1 (z 1 )Im2π5P 4 (z 4 )2π52π5 2π52ππ15P 3 (z 3 )Re5P 2 (z 2 )[2m](b)[5m]Least value of z + 3− i = z5+ 3− i =( Note z + 3− i = z −( − 3+i))13i π152e + 3 − i = 1.19 (2 d.p.)3ππw+ 2− 2i = w−( − 2+ 2i) < 2 and − ≤arg ( w −( − 1+ 3i) ) ≤−4 4© RI 2011 2011 RI Year 6 Preliminary Examinations/H2 Mathematics 9740 – Page 12 of 13

Imw −( − 2+ 2i) = 24(−1, 3)(−2, 2)223π4−4−23πarg ( w −( − 1+ 3i) ) =−41π42Required regionπarg ( w − ( − 1+ 3i) ) =−4Reπ< arg( w)